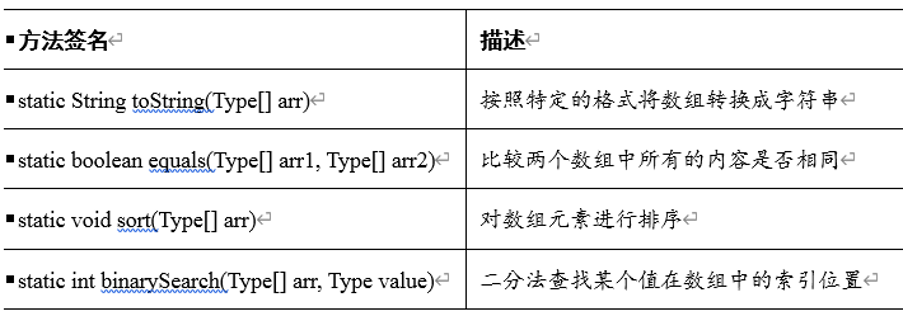
背诵
线性表
-
前驱:
-
后继
-
表长:
-
空表:
-
首元结点:
-
头结点:
-
头指针
-
线性表的结构特点,除了第一个和最后一个元素外,每个节点都只有一个前驱和后继。
-
线性表的存储方式:
栈与队列
-
顺序栈
-
链栈
-
链队列
-
栈与队列存储数据
-
栈的应用:
-
循环列表判队空、队满条件,
串
- 串是一段有限长的字符序列,由一对单引号相扩
- 通常以串的整体进行操作
- 串的三种存储方式:定长存储、堆分配存储、块链存储
数组与广义表
- 一维数组:相同类型的数据元素的集合
- 二维数组顺序存储方式:行优先顺序、列优先顺序
- 特殊矩阵:对称矩阵、三角矩阵、稀疏矩阵
- 稀疏矩阵存储方式:三元顺序法,行逻辑链接的三元组、十字链表法
- 稀疏矩阵转置时间复杂度:\(\mathcal{O}(column*t)\)快速转置时间复杂度\(\mathcal{O}(column+t)\)
- 广义表:
树与二叉树
-
树是n个结点的有限集;有且仅有一个跟结点,除了根结点外其余结点可分为互不相交的有限集合。
-
叶子结点、终端结点:度为0 的结点;
度:结点拥有的子树个数;
树的结点:包含一个数据元素及若干指向其子树的分支;
非终端结点、分支结点:度为0的结点;
内部结点:除了根节点之外;
树的度是树内各结点度的最大值。
树的度是各结点度的最大值;
孩子,双亲;
兄弟;
祖先:从根结点到该结点所经分支的所有结点;
堂兄弟:双亲在同一层;
深度、层数
-
二叉树的性质:
- 第 i 层至多\(2^{i-1}\) 个结点;
-
存储结构:顺序存储结构、链式存储结构:二叉链表、三叉链表
-
二叉树遍历:先序,中序,后序
int preordertraverse(Bitree T,status(*visit)(Telemtype e)){if(T){if(visit(T->data))if(preordertraverse(T->lchild,visit))if(preordertraverse(T->rchild,visit))return OK;return ERROR;}else return OK; }void Inorder(biTree T){stack S;InitStack(&S);BiTreeNode *p=T;while(p!=NULL||!EmptyStack(&S)){if(p->lchild){push(&S,p);p=p->lchild;}else{pop(&S,p);visit(p);p=p->rchild;}}return ok; }-
线索二叉树
求得结点的一个线性序列;前驱、后继的指针;称为线索;
线索链表的结点:增加两个标志域,Lchild指针Link0;Lchild指针指向前驱/后继,线索Thread 1;
-
void inordertraverse_thr(Bitree T,void(*visit)()){p=T->lchild;while(p!=T){while(p->LTag==Link){p=p->lchild;}visit(p->data);while(p->RTag==Tread&&p->rchild!=T){ p=p->rchild;visit(p);}p=p->rchild;}
}
node* pre=null;\\全局变量
void init(Bitree T){BiTree Th = (BiTree)malloc(sizeof(BiTNode));Th->ltag = Link;Th->rtag = Thread;Th->rchild = Th;if (!T) Th->lchild = Th;else {Th->lchild = T;pre = Th;InOrderThreading(T, visit); // 开始线索化// 最后处理,连接头节点pre->rtag = Thread;pre->rchild = Th;Th->rchild = pre;}
}
void inorder(Bitree T,status(*visit)(Telemtype e),node * p){if(!p){inordered(p->lchild,visit)if(p->lchild==NULL) {p->Ltag=Thread; p->lchild=pre;}if(pre->rchild==NULL||pre->Ltag==Thread){pre->Ltag=Thread;pre->rchild=p;}pre=p;inordered(p->rlchid,visit);}return ;
}
树的三种存储结构:双亲表示法、孩子链表表示法,二叉链表存储方式;
树的遍历:先根遍历、后跟遍历、按层次遍历;
| 森林 | 树 | 二叉树 |
|---|---|---|
| 先序遍历 | 先根遍历 | 先序遍历 |
| 中序遍历 | 后根遍历 | 中序遍历 |
哈夫曼树:n-1次,二叉树,实现数据压缩,最小编码长度,
图
-
图是由一个顶点集V和一个弧VR构成的数据结构
-
网:弧或边带权的图分别称为有向网或无向网
-
子图:
-
完全图:含有e=n(n-1)/2的无向图叫做完全图;类似定义有向完全图
-
稀疏图:边或者弧的个数\(<n*logn\)稀疏图,反之则为稠密图
-
出度,入度
-
简单路径:序列中顶点不重复出现的路径;
-
简单回路:序列中第一个顶点和最后一个顶点相同的路径
-
强连通图:对有向图,若任意两个顶点之间都存在一条有向路径;
-
各个强连通子图成为强连通分量;
-
无向图:连通图,非连通图:各个连通子图成为连通分量
-
图的存储表示:邻接矩阵、邻接表、十字链表
-
图的两种遍历方式:深度遍历和广度遍历:
void DFS(Graph G,int v){visit[v]=True;visitFunc(v);for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w)){if(!visit[w]) DFS(G,w);} }void DFStraverse(Graph G,Status(*visit)(int v)){visitFunc=visit;for(v=0;v<G.vexnum;++v){visit[v]=False;}for(v=0;v<G.vexnum;v++){if(!visit[v]) DFS(G,v);} }void BFS(Graph G,int v){visited[v]=True;visitFunc(v);Enqueue(v,&Q);while(!isempty(&Q)){ EnQueue(&Q);for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w)){if(!visited(w)){visit(w);visited[w]=False;Enqueue(&Q,w);}}} }void DFStraverse(Graph G,Status(*visit)(int v)){visitFunc=visit;for(v=0;v<G.vexnum;++v){visited[v]=False;}for(v=0;v<G.vexnum;v++){if(!visited[v]) DFS(G,v);} } -
最小生成树:在e条带权的边中选取n-1条边(不构成回路),使权值之和为最小。
-
生出树:不要求权值最小
-
prim算法
void MIniSpanTree_P(MGraph G,VertexType u){bool visited[G.vertexnum]={False};visited[u]=True;int dist[G.vertexnum]=G.adj[u];int cnt=0;while(cnt<G.vertexnum){cnt++;int min=-1;int dist_min=INT_MAX;for(int i=0;i<G.vexnum;i++){if(!visited[i]&&(dist[i]<dist_min||!min=-1)) {min=j;dist_min=dist[i];}dist[j]=dist_min;visited[min]=True;for(int i=0;i<G.vexnum;i++){if(!visited[i]&&dist[i]<G.adj[i][min]) dist[i]=G.adj[i][min];}} } -
Kruskal算法
-
dijstra算法:\(\forall v\in V~~ dist[u]=min \{ dist[u],dist[v]+w_{v->u} \}\)
-
拓扑排序:检查是否出现
按照有向图给出的次序关系,将图中顶点排成一个线性序列,对于有向图中没有限定次序关系的顶点,则可以人为加上任意的次序关系;
CountInDegree(G,indegree);//求顶点入du InitStack(S); for(int i=0;i<G.vernum;i++){if(!indegree[i]) Push(S,i); } count=0; while(!IsEmpty(S)){Pop(S,v);count++;printf(v);for(w=Firstadj(v);w;w=Nextadj(G,v,w)){indegree(w)--;if(!indegree[w]) Push(S,w);} } if(count<G.vexnum) printf("存在回路"); -
关键路径
-
ve(源点)=0;
最早发生时间:
\(ve(k)=Max\{ve(j)+dut(<j,k>)\}\)
最迟发生时间:
\(vl(j)=Min\{vl(k)-dut(<j,k>)\}\)
活动(弧)最早开始时间e(i)=ve(j);最晚开始时间l(i)=vl(k)-dut(<j,k>)
查找表
-
查找表是由同一类型的数据元素构成的集合
-
功能:查询、检索、插入、删除
-
查找表分为静态查找表:查询和检索功能的查找表
动态查找表:将查询结果不在查找表中的数据元素插入;或者删除;
-
数据元素或记录中某个数据项的值,用以标识一个数据元素;若此关键字可以识别唯一的一个记录,称之为主关键字;弱关键字能识别若干记录,称为次关键字
-
查找:确定一个其关键字等于给定值的数据元素或记录;
-
静态查找表
-
顺序表查找
int location(SqList L,ElemType& e,Status(*compare)(ElemType,ELemtype)){k=1;p=L.elem;while(k<=L.length&&!(*compare)(*p++,e)) k++;if(k<=L.length) return k;else return 0; }int search_Seq(SSTable ST,KeyType key){ST.elem[0].key=key;for(int i=ST.length;ST.elem[i].key!=key;i--);return i; } -
折半查找
int Search_Bin(SSTable ST,KeyType key){int low=1;high=ST.length;while(low<=high){mid=(low+high)/2;if(key==ST.R[mid].key) return mind;else if(key<ST.R[mid].key) high=mid-1;else {low=mid+1;}}return 0; } -
索引顺序表(分块查找)
查找过程:
-
由索引确定记录所在区间;
-
在顺序表的某个区间内进行查找;
特点:缩小区间
索引顺序查找的平均查找长度=查找索引的平均查找长度+查找顺序表的平均查找长度;
-
-
查找表的特性
查找 插入 删除 无序顺序表 \(\mathcal{O}(n)\) \(\mathcal{O}(1)\) \(\mathcal{O}(n)\) 无序线性链表 \(\mathcal{O}(n)\) \(\mathcal{O}(1)\) \(\mathcal{O}(1)\) 有序顺序表 \(\mathcal{O}(\log(n))\) \(\mathcal{O}(n)\) \(\mathcal{O}(n)\) 有序线性链表 \(\mathcal{O}(n)\) \(\mathcal{O}(1)\) \(\mathcal{O}(1)\)
-
-
动态查找表
-
二叉排序树(二叉查找树)
-
左子树若不空,则左子树上所有结点的值均小于根节点的值;
-
若右子树不空,则右子树上所有结点的值大于根节点的值
-
它的左右子树都为二叉排序树
Status SearchBST(BiTree &T,KeyType key,BiTree &f,BiTree &p){if(!T){p=f;return FALSE;}else if(EQ(key,T->data.key)){p=T;return TURE;}else if(LT(key,T->data.key))SearchBST(T->lchild,key,T,p);else SearchBST(T->rchild,key,T,p); }void InsertBST(BSTree &T,ElemType e){if(!SearchBST(T,e.key,NULL,p)){if(!T){S=new BSTNode;S->data=e;S->lchild=S->rchild=NULL;T=S;}else if(e.key<T->data.key) InsertBST(T->lchild,e);else if(e.key>T->data.key) InsertBST(T->rchild,e);} }void CreatBST(BSTree &T){T=NULL;cin>>e;while(e.key!=ENDFALG){InsertBST(T,e);cin>>e;} }Status DeleteBST(BiTree &T,KeyType key){SearchBST(T,e.key,NULL,p);if(!T) return FALSE;else Delete(p); }void Delete(BiTree &p){if(!p->rchild){q=p;p=p->lchild;free(q);}else if(!p->lchild){q=p;p=p->rchild;free(q);}else{q=p;s=p->lchild;while(s->rchild){q=s;s=s->rchild;}p->data=s->data;if(q!=p) q->rchild=s->lchild;else q->lchild=s->lchild;free(s);} }时间复杂度: \(n*\mathcal{O}(\log(n))\)
-
-
二叉平衡树
- 二叉平衡树使二叉排序树的另一种形式,其特点为树中每个结点的左右子树深度之差绝对值不大于1;
- 深度为\(h\)的二叉平衡树中所含结点最小值\(N_{h}=F_{h+2}-1\)
-
-
哈希表
-
哈希表:记录在表中的位置和它的关键字之间不存在一个确定的关系
查找的过程为给定值依次和关键字集合中各个关键字进行比较,查找的效率取决于和给定值进行比较的关键字个数。
-
哈希函数是一个映射。关键字的集合映射到某个地址集合上,只要这个地址结合的大小不超过允许范围。
-
哈希函数是一个压缩映像,容易存在冲突现象。
-
哈希函数的构造方法:
-
直接定址法:适用于地址集合大小等于关键字集合的大小。
\(H(key)=key~~or~~H(key)=a*key+b\)
-
数字分析法:分析关键字集中的全体,并从从中提取分布均匀的若干位或他们的组合作为地址。适用于:能预先估计出全体关键字的每一位上各种数字出现的频度。
-
平方取中法:以关键字的平方值的中间几位作为存储地址。适合于关键字中的每一位都有某些数字重复出现频度很高的现象。
-
折叠法:将关键字分割成若干部分,然后取它们的叠加和为哈希地址。适用于数字位数特别的的情况
-
除留余数法
-
随机数法\(H(key)=Random(key)\)
-
-
处理冲突的方法:为冲突的地址寻找下一个哈希地址
-
开放定址法:
-
\(H_{0}~H_{1}\dots H_{s}\)
\(H_{i}=(H(key)+d_{i})~~mod(m)\)
\(d_{i}\)三种取法:
-
线性探测再散列
\(d_{i}=c*i\)
-
平方探测再散列
\(d_{i}=1^{2},-1^{2},2^{2},-2^{2}\dots\)
-
随机探测再散列
\(d_{i}\)是一组伪随机数列或者\(d_{i}=i*H_{i}(key)\)
注意\(d_{i}\)应该具备完备性;\((m,d_{i})=1\)
-
-
-
链地址法
-
哈希表的查找
int hashsize[]={997,...}; typedef struct{ElemType *elem;int count;int sizeindex; }HashTable; #define SUCCESS 1 #define UNSUCCESS 0 #defint DUPLICATE -1 status SearchHash(HashTable H,KeyType K,int &p,int &c){p=Hash(K); while(H.elem[p]!=NULLKEY&&!EQ(K,H.elem[p].key)) return SUCCESS;else return UNSUCCESS; }Status InsertHash (HashTable &H,Elemtype e){c=0;if(HashSearch(H,e.key,p,c)==SUCCESS)return DUPLICATE;else if(c<hashsize[H.sizeindex]/2){H.elem[p]=e;H.count++;return OK;}else RecreateHashTable(H); }//inserthash -
装载因子:$\alpha=n/m $
-
-
排序
-
排序:将无序的记录序列调整为有序的记录序列
-
外部排序:不需要访问外存便可以完成,此类问题成为内部排序
-
内部排序:不可能只在内存中
-
内部排序方法:插入类、交换类、选择类、归并类、其他方法
-
- 插入类:将无序子序列的一个或几个记录插入到有序序列中
- 交换类:通过交换无序序列中的记录从而得到其中关键字最小或最大的记录,并将它加入到有序子序列中
- 选择类:从记录的无序子序列中选择关键字最小或最大的记录,并将它加入到有序子序列中
- 归并类:通过归并两个或两个以上的记录有序子序列,逐步增加记录有序序列的长度
-
实现一趟插入排序:

-
方法:直接插入排序、折半插入排序、希尔排序
-
希尔排序:
基本思想:对待排序记录序列先作宏观调整,再做微观调整;将记录序列分为若干个子序列,分别对每个子序列进行插入排序。
void ShellInsert(SqList &L,int dk){for(int i=dk+1;i<n;i++){if(L.r[i]<L.r[i-dk].key){L.r[0].L.r[i];for (j=i-dk; j>0&&(L.r[0].key<L.r[j].key); j-=dk)L.r[j+dk] = L.r[j]; // 记录后移,查找插入位置L.r[j+dk] = L.r[0]; // 插入}} } void ShellSort (SqList &L, int dlta[], int t) { // 增量为dlta[]的希尔排序for (k=0; k<t; ++t)ShellInsert(L, dlta[k]);//一趟增量为dlta[k]的插入排序 } // ShellSort -
交换排序:
-
起泡排序,一趟快速排序,快速排序
-
起泡排序
void bubblesort(Elem R[],int n){int i=n;while(i>1){int lastxchangeIndex=1;for(int j=1;j<i;j++){if(R[j+1].key<R[j].key){swap(&R[j+1].key,&R[j].key);lastExchangeIndex=j;}i=lastExchangeIndex;}} } -
一趟快速排序
目标:找一个目标,以他的关键字为枢轴,凡其关机子小于枢轴的记录均移动到该记录之前,反之,移动掉该记录之后。
int partition(RedType R[],int low,int high){R[0]=R[low];pivotkey=R[low].key;while(low<high){ while(low<high&&R[high].key>=pivotkey) --high;R[low]=R[high];while(low<high&&R[low].key<=pivotkey)++low;R[high]=R[low];}R[low]=R[0]; return low; }void QSort(RedType &R[],int s,int i){if(s<t){pivotloc=Partition(R,s,t);Qsort(R,s,pivotloc-1);Qsort(R,s,pivotloc+1,t);} }
-
-
选择排序

-
简单选择排序
-
堆排序
void HeapAort(HeapType &H){for(i=H.length/2;i>0;i--){HeapAdjust(H.r,i,H.length);}for(i=H.length;i>1;i--){swap(H.r[1],H.r[i]) HeapAdjust(H.r,1,i-1);} }void HeapAdjust(RcdType &R[],int s,int m){rc=R[s];for(int j=2*s;j<=m;j*2){if(j<m&&R[j].key<R[j+1].key) j++;if(rc.key>=R[j].key) break;R[s]=R[j];s=j;}R[s]=rc; }
-
-
归并排序
void Merge(RcdType SR[],RcdType TR[],int i,int m,int n){for(int j=m+1,int k=i;i<m&&j<=n;++k){if(SR[i].key<=SR[j].key) TR[k]=SR[i++];else TR[k]=SR[j++];}while(i<=m) TR[k]=SR[i++];while(j<=n) TR[k]=SR[j++];for(int i=m;i<=n;i++){SR[i]=TR[i];} } void Msort(RcdType SR[],RcdType TR1[],int t){if(s==t) TR1[s]=SR[s];else{m=(s+t)/2;Msort(SR,TR1,s,m);Msort(SR,TR2,m+1,t);Merge(SR,TR1,s,m,t);} } void MergeSort(SqList &L){Msort(L.r,L.r,1,L.length); }
-
-
时间复杂度 空间复杂度 稳定性 直接插入排序 \(\mathcal{O}(n^{2})\) \(\mathcal {O}(1)\) 稳定 快速排序 \(\mathcal{O}(n*\log n)\) \(\mathcal {O}(\log n)\) 不稳定 起泡排序 \(\mathcal{O}(n^{2})\) \(\mathcal {O}(1)\) 稳定 归并排序 \(\mathcal{O}(n*\log n)\) \(\mathcal {O}(n)\) 稳定 简单选择排序 \(\mathcal{O}(n^{2})\) \(\mathcal {O}(1)\) 不稳定 堆排序 \(\mathcal {O}(n*\log n)\) \(\mathcal {O}(1)\) 不稳定 待排序序列已经有序时,直接插入排序和起泡排序达到\(\mathcal{O}(n)\)
快速排序为\(\mathcal{O}(n^2)\)
简单选择排序、堆排序、归并排序时间性能不随记录序列关键字分布而改变
希尔排序不稳定;
基于关键字的排序方法最快\(\mathcal{O}(n*\log n)\)