原题链接:https://www.luogu.com.cn/problem/P4587
题意解读:对于序列a[n],查询m个区间[l,r]数值对应集合的神秘数。集合 S 的神秘数定义为最小的不能被 S 的子集的和表示的正整数。
解题思路:
对于区间[l,r],从小到大将数值选入集合,来观察神秘数的变化,设S当前的神秘数为ans。
当下一个要选入的数为x时,
如果x > ans,加入x也不会影响集合的神秘数,ans不变。
因为,x加入前,S子集和可以表示出[1,ans-1]的数,x>ans,仍然无法表示出等于ans的数;
所以,S的神秘数还是ans。
如果x <= ans,加入x会影响集合的神秘数,ans = x + ans。
加入x前,S子集和表示的数范围是[1,ans-1],加入x后可以表示范围多了[x+1,x+ans-1],再算上x自己;
加入x后,S子集和表示数的范围变成[1,ans-1] ∪ [x] ∪ [x+1,x+ans-1] = [1,x+ans-1];
所以ans变成x + ans。
这样,可以通过将[l,r]范围的数值从小到大选入集合S,ans不断更新,得到最终结果,总体时间复杂度O(mn)。
如何优化?
设集合S当前已选入数都没有超过maxs,也就是下一个加入集合的数必须>=maxs+1,当前神秘数为ans。
不难分析得到,下一个要选入的数,必须再[maxs+1, ans]范围内,才能影响ans,因为<=maxs的数已经加入过了。
那么,[maxs+1, ans]范围的数对神秘数ans的影响是什么呢?
假设[maxs+1, ans]范围有三个数x,y,z,满足maxs+1<=x<y<z<=ans
对于x,maxs变成x,神秘数变成x+ans
对于y,maxs变成y,神秘数变成x+y+ans
对于z,maxs变成ans(<=ans的数都被选完了),神秘数变成x+y+z+ans
根据以上分析,[maxs+1, ans]范围的数对神秘数的影响就是神秘数变成[maxs+1, ans]数值和sum+ans,之后maxs变成ans。
当前,神秘数要改变,前提是[maxs+1, ans]范围和不为0,如果为0,就得到了最终的神秘数。
用范围求和来代替一个一个的加入集合过程,时间复杂度得到了优化。
因此,本题核心流程用形式化的描述为:
在[l,r]范围查询值域区间[maxs+1,ans]的和res,初始maxs=0,ans=1
持续处理,如果res>0,mas=ans,ans=res+ans
直到res==0,输出ans。
要实现[l,r]范围内的[mas+1,ans]区间和查询,可以采用可持久化线段树。
尽管数值的取值范围较大,不提前build线段树,借助于动态开点,就不需要进行离散化处理。
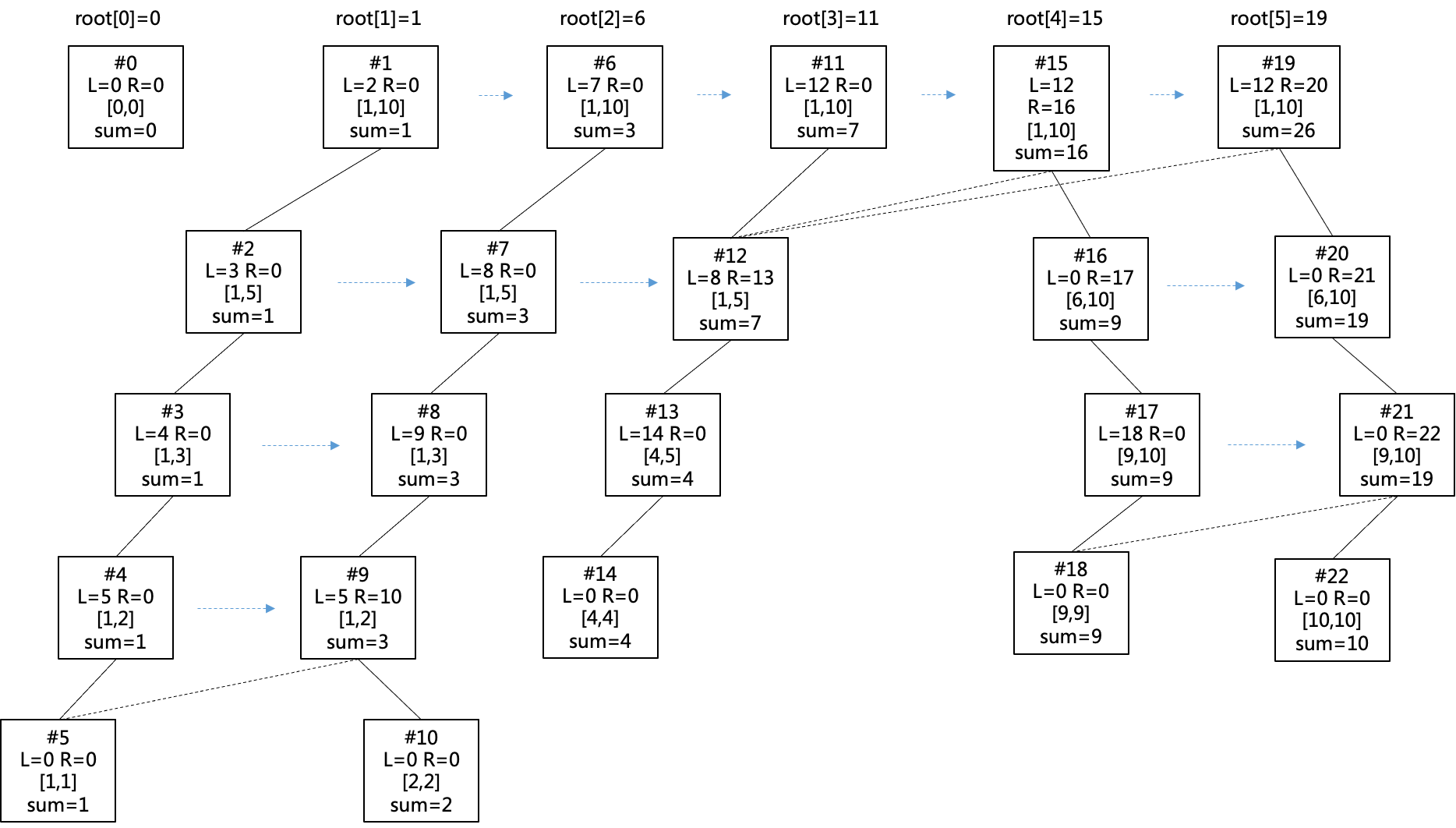
对于序列1 2 4 9 10动态开点建立的线段树如图所示,请自行比较与提前build再复制的区别,参考:https://www.cnblogs.com/jcwy/p/18630532
100分代码:
#include <bits/stdc++.h>
using namespace std;const int N = 100005;
struct Node
{int L, R; //左、右子节点编号int sum;
} tr[N * 32];
int root[N], idx; //根节点,节点编号
int a[N], maxa;
int n, m;//在根为pre的权值线段树中,将节点[x,x]到根节点复制一份,并把所有sum增加一个x
int update(int pre, int l, int r, int x)
{int u = ++idx;tr[u].L = tr[pre].L;tr[u].R = tr[pre].R;tr[u].sum = tr[pre].sum + x;if(l == r) return u;int mid = l + r >> 1;if(x <= mid) tr[u].L = update(tr[pre].L, l, mid, x);else tr[u].R = update(tr[pre].R, mid + 1, r, x);return u;
}//在left,right权值线段树中,查询值域范围[vl,vr]的元素之和
int query(int left, int right, int l, int r, int vl, int vr)
{if(l >= vl && r <= vr) return tr[right].sum - tr[left].sum;else if(l > vr || r < vl) return 0;else {int mid = l + r >> 1;return query(tr[left].L, tr[right].L, l, mid, vl, vr) + query(tr[left].R, tr[right].R, mid + 1, r, vl, vr);}
}int main()
{cin >> n;for(int i = 1; i <= n; i++){cin >> a[i];maxa = max(maxa, a[i]);}for(int i = 1; i <= n; i++) root[i] = update(root[i - 1], 1, maxa, a[i]);cin >> m;int l, r;while(m--){int maxs = 0, ans = 1, res;cin >> l >> r;while(true){res = query(root[l - 1], root[r], 1, maxa, maxs + 1, ans);if(!res) break;maxs = ans, ans = res + ans;}cout << ans << endl;}return 0;
}