论文阅读日记

阅读一点论文，主要是 \(k-clique\) 计数相关的。

Listing k-cliques in Sparse Real-World Graphs

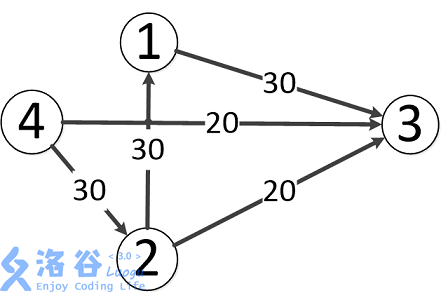
这篇比较基础，涉及到了很基本的团计数思想。基本就是说，将这个图的边定向形成一个 \(DAG\) 后，可以按照树的隐式结构，访问所有可能包含团的子集。具体的说，每次递归，传的参就是一个顶点的集合。随后从这个顶点的集合中枚举每个顶点，在选取这个顶点所有的在目前这个集合里的邻居作为新的点的集合继续去遍历。

但很明显，如何定向是影响复杂度的一个关键因素。这篇论文提出非常高效的定向算法，即按照 \(core-ordering\) 去定向。这个也叫 \(degeneracy-ordering\) ，从后者这个名字可以看出来，意思就是每次选取原无向图中度数最小的点删去并加入 \(order\) ，于是相邻的边也被删掉了，重复这个过程即可。做完后这个 \(DAG\) 中最大的出度数叫做这个图的 \(core-value\) ，也叫 \(degeneracy\) 。可以证明 \(degeneracy\) 是所有可能形成的 \(DAG\) 中最小的最大出度数。

关键就在于限制这个最大出度数，因为这个最大出度数显著影响了递归树的分叉数，复杂度也是根据这个限制的。最终这个算法的时间复杂度是 \(O\left(km\left(\frac{c(G)}{2}\right)^{k-2}\right)\) 。