1.1 可压缩流：等熵流动

1.1 可压缩流：等熵流动

热力学复习

理想气体：认为分子间的碰撞是弹性的，没有热、动量损失。

\[\begin{equation}p=\rho RT\end{equation} \]

内能：给定体积内所有分子包含能量的总和。

比内能（内能/质量）e与比焓h：

\[\begin{equation}h=e+pv\end{equation} \]

这里p是压强，v是比体积，\(v=\frac{1}{\rho}\)。

对于理想气体，e和h都是关于温度的函数；而对于卡诺热力学理想气体，比热是常数：

\[\begin{equation} \begin{align*} e&=c_v T\\ h&=c_p T \end{align*} \end{equation} \]

比热和气体常数有关：

\[\begin{equation} c_p-c_v=R \end{equation} \]

比热容比\(\gamma\)是：

\[\begin{equation} \gamma=\frac{c_p}{c_v} \end{equation} \]

基于公式4和5，有：

\[\begin{equation}c_p=\frac{\gamma R}{\gamma-1}~\text{and}~c_v=\frac{R}{\gamma-1} \end{equation} \]

热力学四大定律：

• 第0定律：热冷平衡律，当两个系统和第三个系统达到热平衡时，这两个系统之间也处于热平衡状态。

• 第1定律：能量守恒

  \[\begin{equation}\delta e=\delta q+\delta w \end{equation} \]

• 第二定律：熵（entropy，衡量系统无序程度的量）在一个孤立系统中，总是趋向于最大化（一直增加）。

• 第三定律：在绝对零度时，完整的晶体结构具有恒定的熵。

基本概念

热力学

绝热过程（adiabatic process）：关于某个系统或控制体积，没有热量流出或流入。

可逆过程（reversible process）：不会在过程中向介质或周围环境损失能量的过程。不会发生由于粘性、热导率、质量扩散等耗散现象。

等熵（理想）过程：既绝热又可逆的过程。

等熵过程下不同状态量之间的关系：

\[\begin{equation}\frac{p_2}{p_1}=\left(\frac{\rho_2}{\rho_1}\right)^\gamma=\left(\frac{T_2}{T_1}\right)^{\frac\gamma{\gamma-1}} \end{equation} \]

引入新定义：可压缩性（compressibility）\(\tau\)，表征气体体积如何随着外界压强改变。

\[\begin{equation}\tau=-\frac{1}{v}\left(\frac{dv}{dp}\right) =\frac{1}{\rho}\left(\frac{d\rho}{dp}\right) \end{equation} \]

注意，这里\(v=\frac{1}{\rho}\)。

但特别注意：恒定密度并不能直接定义流体是不可压缩的。

马赫数和雷诺数

马赫数（Mach number）：把速度V和当地声速a联系起来。

\[\begin{equation}\begin{aligned}M&=\frac{V}{a}\\\\a&=\sqrt{\gamma RT}\end{aligned} \end{equation} \]

这里，我们使用到了绝热指数\(\gamma = 1.4\)（干燥空气），气体常数\(R=287\)和当地空气温度\(T\)，这和热力学有联系。

马赫数用于衡量气体动力学当中，可压缩性的影响。

此外，流动是有粘性的，定义动力粘度\(\mu\)和运动粘度\(\nu\)，其中\(\mu = \rho \nu\)。

从能量守恒的角度来说，粘性的影响就是造成损失。

受粘性影响，会形成边界层。

用于衡量粘性影响的数叫雷诺数（Reynolds number，注意这里不是i而是l），其定义式为：

\[\begin{equation}Re=\frac{UL}{\nu}=\frac{\rho U L}{\mu} \end{equation} \]

若题目中说明流体是无粘性的，那么直接忽略粘性效应就好。

等熵流动

基本

接下来我们引入等熵流动（isentropic flow）的概念。

做出如下假设：

• 没有热和功的传导；
• 势能变化可以忽略不计；
• 稳态流动；
• 无粘性流动，即流动位于边界层外。

总结一下就是绝热和可逆。

给出如下对于等熵流动的基本方程：

1. 连续性（质量守恒）：

   \[\begin{equation}\dot{m}=\rho AV=constant \end{equation} \]

2. 动量方程：

   \[\begin{equation} p+\rho V^2=constant \end{equation} \]

3. 能量方程（忽略势能）：

   \[\begin{equation} h+\frac{V^2}{2}=constant \end{equation} \]

   对该方程做进一步解释：

   • 焓的定义：

     \[\begin{equation} H=U+pV \end{equation} \]

     这里，H是焓，U是内能，p是压力，V是体积。

     焓 (Enthalpy) 是一个热力学状态量，表征系统内部的能量，及系统与环境做（压力-体积）功的能力。

   • 比焓：\(h=u+pv\)，相当于给上述焓公式除以质量，代表单位质量的流体所具有的焓。

   • 比动能：\(\frac{V^2}{2}\)​

考虑如下流动条件：

1. 稳态流动（static conditions）

   ​​

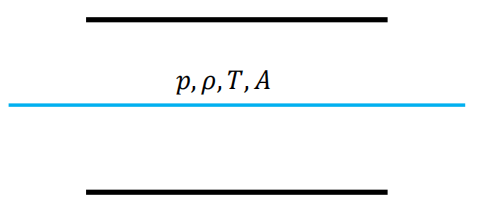
2. 总（滞止）条件，total/stagnation conditions

   ​​

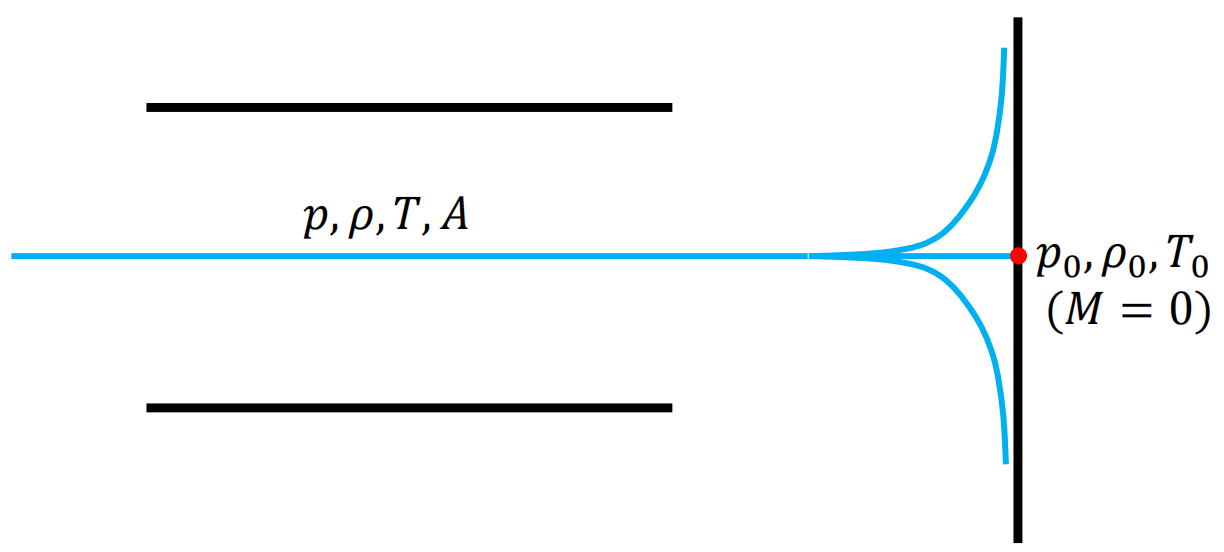
   这里意为，稳态流动出来之后撞上了一堵墙，中间的红点就是滞止点（stagnation point）。

   这种流动的特征：

   • 滞止点处流体速度为0；

   • 流体在滞止点处失去所有动能，转化为内能，导致焓、压力和温度达到最大值；

   • 从流动中的某一点，到滞止点的过程是等熵的，没有热量交换、摩擦等耗散作用；

   • 滞止焓等于流动中任意一点的静焓加动能：

     \[\begin{equation}h_0=h+\frac{V^2}{2} \end{equation} \]

3. 声速（sonic）条件

   ​​

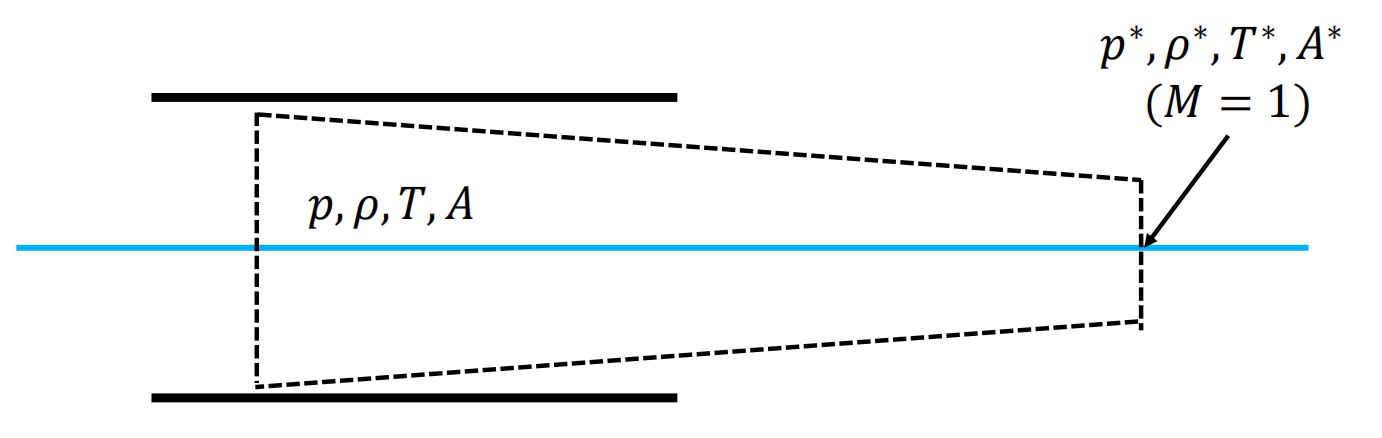
   这个条件将在后面详细分析。

温度，压力和密度比例

选择流线中的任意两点：

​​

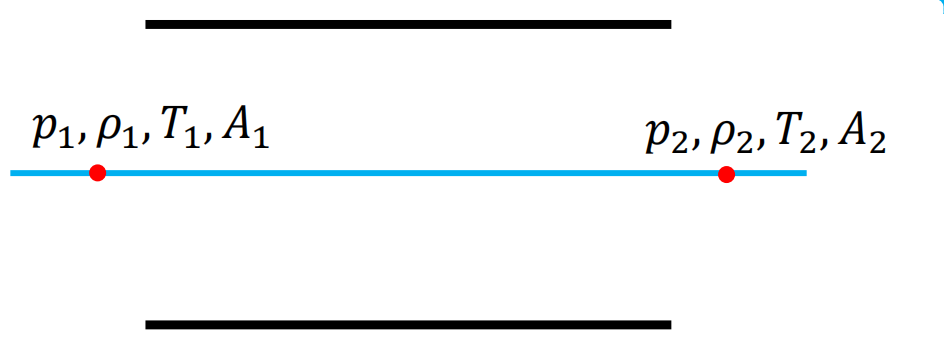
讨论能量方程：

\[\begin{equation}h_1+\frac{V_1^2}{2}=h_2+\frac{V_2^2}{2} \end{equation} \]

据此可以推导出温度比例：

\[\begin{equation}\frac{T_1}{T_2}=\left[1+\left(\frac{\gamma-1}{2}\right)\left(\frac{V_2^2-V_1^2}{a_2^2}\right)\right] \end{equation} \]

若点1处为滞止条件，此时有\(V_1=0\)，那么温度比例变成：

\[\begin{equation}\frac{T_0}{T}=\left[1+\left(\frac{\gamma-1}{2}\right)M^2\right] \end{equation} \]

其中，\(T_0\)表示滞止点温度，T表示流动中的某点的温度。

进一步地，我们寻找滞止点和流动点的压力和温度的关系：

\[\begin{equation}\frac{P_0}{P}=\left[1+\left(\frac{\gamma-1}{2}\right)M^2\right]^{\frac{\gamma}{\gamma-1}} \end{equation} \]

\[\begin{equation}\frac{\rho_0}{\rho}=\left[1+\left(\frac{\gamma-1}{2}\right)M^2\right]^{\frac{1}{\gamma-1}} \end{equation} \]

下图反映出了干燥空气中，随着马赫数增加，压力、密度、温度的比例的增长趋势：

​​

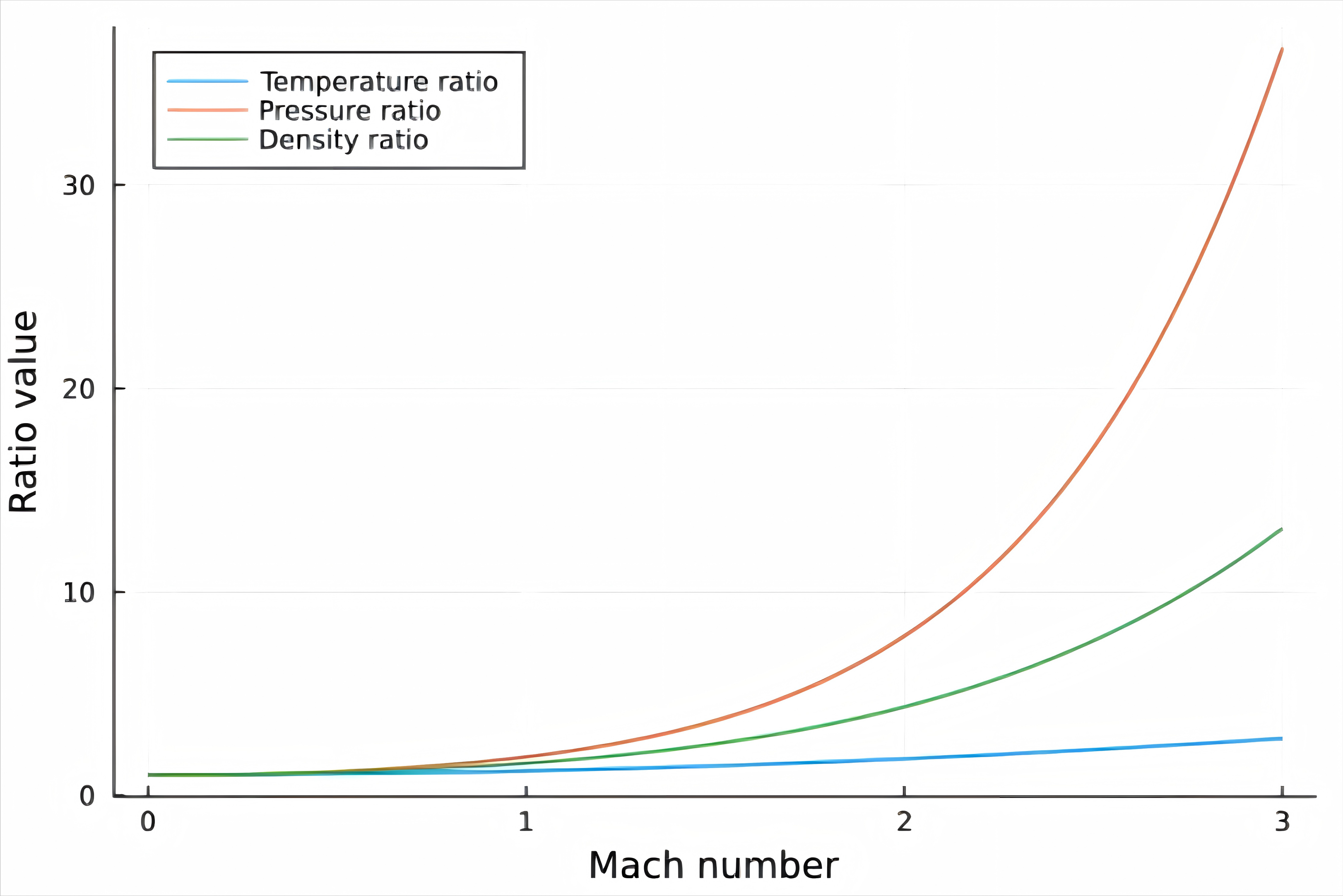
从这里可以看出类似指数函数的趋势，其中，压力的指数是3.5，密度的指数是2.5，温度的指数是1（就差不多是二次函数了）。

需要特别注意：对于等熵流动，总温度恒定（绝热），总压力恒定（可逆），总密度恒定（停滞点处​\(p_0=\rho_0 R T_0\)​ ） 。

例

对于一个马赫数3的可压缩流动，我们可以计算得到滞止流-稳态流动的温度比（或等熵温度比）：

\[\begin{equation}\begin{gathered}\frac{T_{0}}{T}=\left[1+\left(\frac{\gamma-1}{2}\right)M^{2}\right]\\=\left[1+\left(\frac{1.4-1}{2}\right)3^{2}\right]\\=[1+0.2\times3^{2}]=[1+0.2\times9]=2.8\end{gathered} \end{equation} \]

实际上，对于特定的马赫数，可以直接查表得到当前马赫数下的滞止温度、压力、密度比。

‍