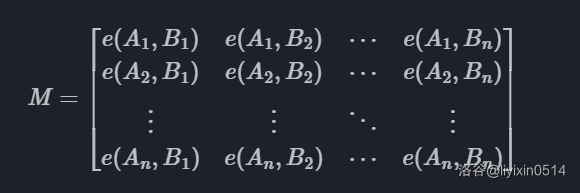首先对于这个问题有一个很直观的做法是直接 DP。
即设 \(f_i\) 为已经划分出 \([1, i]\) 部分,且最后一段段尾为 \(i\) 的方案数。
但是这个题还涉及到了有的点可以不染色的情况,所以再设 \(g_i\) 为已经划分出 \([1, i]\) 部分,且下一段为 \(i + 1\) 开头的方案数。
对于转移 \(f\),就可以考虑枚举上一段的段头:\(f_i = \sum\limits_{j = 0}^{i - 1} \operatorname{check}(j + 1, i)\times g_j\),其中 \(\operatorname{check}(l, r)\) 代表 \([l, r]\) 这段区间能否按照题目所述合法的染色。
对于转移 \(g\),就直接考虑 \(i\) 这个位置是否要不染色:\(g_i = f_i + [s_i = \texttt{X}]g_{i - 1}\)。
对于转移 \(g\) 是 \(\mathcal{O}(n)\) 的,于是只需要考虑优化 \(f\) 的转移就行了。
考虑拆一下这个 \(\operatorname{check}(i, j)\):
-
一个条件是 \((j - i)\bmod 2 = 0\),这个比较好做,只需要根据 \(\bmod\ 2\) 分开维护就行。
-
另一个条件是 \(\forall k\in [i, i + \frac{j - i}{2}), s_k = \texttt{X}\lor s_k = \texttt{R}, \forall k\in [i + \frac{j - i}{2}, j], s_k = \texttt{X}\lor s_k = \texttt{B}\)。
因为这里的 \(s_k\) 是两者均可的方式,加上字符集只有 \(\texttt{XBR}\),于是考虑把条件转化为补集:
\(\forall k\in [i, i + \frac{j - i}{2}), s_k \ne \texttt{B}, \forall k\in [i + \frac{j - i}{2}, j], s_k \ne \texttt{R}\)。这说明,对于 \(i\) 后最小的满足 \(s_k = \texttt{B}\) 的 \(k\),\(k\) 不能被划入 \([i, i + \frac{j - i}{2})\) 的范围内,即 \(k\ge i + \frac{j - i}{2}\),那就有 \(j\le 2k - i\);同样的,对于 \(j\) 找到 \(j\) 之前最小的满足 \(s_{k'} = \texttt{R}\) 的 \(k'\),有 \(i\ge 2k' - j\)。
于是只要同时满足 \(j\le 2k - i, i\ge 2k' - j\),就满足了这个条件。
于是接下来转化成了,对于下标 \(\bmod\ 2\) 考虑。
并且对于转移中的 \(\operatorname{check}(i + 1, j)\),对于 \(i + 1\) 有一个关于 \(j\) 合法区间 \([i + 1, r_{i + 1}]\),对于 \(j\) 有一个关于 \(i\) 的合法区间 \([l_j, j]\),若 \(i + 1,j\) 都合法则合法。
那么对于这个问题,可以把 \(i + 1\) 的限制和 \(j\) 的限制分开考虑,最后合并。
考虑往右扫 \(j\),并且同时用一个线段树维护对于 \(j\in [i + 1, r_{i + 1}]\) 的 \(g_i\) 的和。
那么此时线段树里维护的值就保证了已经满足了 \(i + 1\) 的限制,接下来只需要考虑第二步 \(i + 1\in [l_j, j]\) 的限制,那么这只需要在线段树上区间求和就可以了。
对于如何维护线段树上的 \(i + 1\),考虑因为 \(i + 1\) 的合法区间是 \([i + 1, r_{i + 1}]\),于是可以在 \(i + 1\) 时加入 \(g_i\),在 \(r_{i + 1} + 1\) 时撤销 \(g_i\) 的贡献。
然后就做到了 \(\mathcal{O}(n\log n)\) 的复杂度。
值得一提的是,这个方法继续优化是可以做到 \(\mathcal{O}(n)\) 的。
考虑到对于 \(j\to j + 1\),\(l_{j + 1}\) 与 \(l_j\) 的区别。
能够发现的是,要么 \(l_{j + 1} = l_j - 2(s_{j + 1}\not = \texttt{B})\),要么 \(l_{j + 1} = j + 1(s_{j + 1} = \texttt{B})\)。
于是可以直接用一个指针扫 \(l_j\) 并维护当前信息,对于第一种情况每一轮只会扫 \(\mathcal{O}(1)\) 个位置,对于第二种情况直接清空就可以了。
对于 \(i + 1\) 的撤销,因为每个位置只会撤销一次,直接一起把贡献撤销了就可以了。
于是这样做的复杂度是 \(\mathcal{O}(n)\)。
下面给出的是 \(\mathcal{O}(n\log n)\) 的做法,对于 \(l, r\) 的计算会稍微有点偏差,但是可以知道这是没有问题的。
#include<bits/stdc++.h>
constexpr int mod = 1e9 + 7;
constexpr int maxn = 5e5 + 10;
int n; char s[maxn];
int wR[maxn], wB[maxn];
int f[maxn], g[maxn];
struct segtr {int tr[maxn * 4];inline void update(int x, int y, int k = 1, int l = 0, int r = n) {(tr[k] += y) >= mod && (tr[k] -= mod);if (l == r) return ;int mid = l + r >> 1;if (x <= mid) update(x, y, k << 1, l, mid);else update(x, y, k << 1 | 1, mid + 1, r);}inline int query(int x, int y, int k = 1, int l = 0, int r = n) {if (x <= l && r <= y) return tr[k];int sum = 0, mid = l + r >> 1;if (x <= mid) sum += query(x, y, k << 1, l, mid);if (y > mid) sum += query(x, y, k << 1 | 1, mid + 1, r);return (sum >= mod) && (sum -= mod), sum;}
} T[2];
std::vector<int> del[maxn];
int main() {scanf("%d%s", &n, s + 1);s[0] = 'R', s[n + 1] = 'B';for (int i = 0, p = 0; i <= n + 1; i++) {if (s[i] == 'R') p = i;wR[i] = p;}for (int i = n + 1, p = n + 1; ~ i; i--) {wB[i] = p;if (s[i] == 'B') p = i;}f[0] = g[0] = 1;for (int i = 0; i <= n; i++) {if (i > 0) {int d = i - wR[i];f[i] = T[i & 1].query(std::max(0, i - d - d), i);(g[i] = (s[i] == 'X' ? g[i - 1] : 0) + f[i]) >= mod && (g[i] -= mod);}int d = wB[i] - i - 1;T[i & 1].update(i, g[i]);if (i + d + d <= n) {del[i + d + d].push_back(i);}for (int j : del[i]) {T[i & 1].update(j, mod - g[j]);}}printf("%d\n", g[n]);return 0;
}