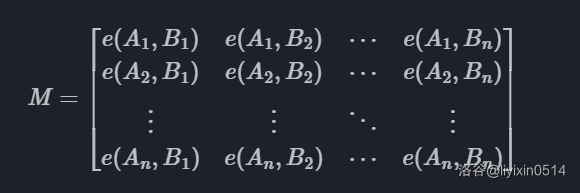线性代数听课笔记-编程知识

线性代数听课笔记

news/2025/1/5 7:25:14/文章来源:https://www.cnblogs.com/hagasei/p/18648836

基本定义

线性空间
线性相关、线性无关
基
矩阵的秩
像空间与核空间（im,ker）
线性代数基本定理

高斯消元

初等行变换相当于左乘一个特殊矩阵。

求逆：对 \((A|I)\) 跑高斯-约旦，即可拿到 \((I|A^{-1})\)。

PLU 分解：

初等行变换里，『一行加到零一行』、『一行乘 k』都可以表示为下三角矩阵，消出来的结果是上三角矩阵。
注意边做边交换和先交换再做本质相同，于是 \(A=PLU\)，其中分别是排列 Permutation、下三角 Lower、上三角 Upper。
实际写代码时不能模拟 L 上的乘积，但是可以边消元边一列一列算。
应用：多组询问解方程 \(Ax=b\)，其中 A 不变，先 n^3 算出 \(A=PLU\)，然后有 \(PLUx=b\Rightarrow Ux=L^{-1}P^{-1}b\) 从而预处理矩阵逆之后可以 n^2 回答一次。

关于有限域：

mod 2（异或方程组）：bitset 优化。
mod p：直接做。
mod 合数：辗转相除。

这里还应该有一个主元法的例题，但是我觉得我会。没啥好写的。

线性基

『动态维护极大线性无关向量组』

每次插入一个向量都依次被主元对应位消元，直到对应位空或消空。类比高斯消元。

一个扩展是类比高斯-约旦消元，找到空位后先用其下方的向量消元、再消元其上方的向量。好处是每个主元只会在线性基里出现一次。

一些简单应用是最大权线性基，第 k 大 xor（这个就是那个扩展），是否包含于线性空间，线性基合并（启发式合并）。

可删线性基：本质还是离线算法（需要知道删除时间），但是比线段树分治少个 log。

插入的时候带上删除时间。每次两个向量消元的时候都判一下、用删除时间更早的往下插入。

线性基求交：转化为核空间的并的核空间，难点在于建出核空间对应的线性基。

贴两张图片，图源维基百科。 pic1 pic2。
大致描述过程：往基向量下方贴一个单位矩阵，将上面的线性基按列变换消元，下面的 I 的后若干列向量就是核空间的一组基。
Quack 的课件里还有一种神秘的凑系数方法，但是复杂度一样的。
注意对压位异或线性基可以位运算加速。

翻维基的时候注意到了一个有趣的结论，不知道有没有用，总之先甩在这里：计算机科学里的浮点数矩阵一定满秩。

Schwartz–Zippel Lemma

对有限域 \(F\) 内的 \(m\) 元 \(n\) 次多项式 \(f(x_1,\dots,x_m)\)，若 \(\forall i,x_i\) 在 \(F\) 内均匀随机取值，则 \(f(x_1,\dots,x_m)=0\) 的概率是 \(n/|F|\)（甚至与 \(m\) 无关）。因为 OI 里的应用一般都取 \(|F|>10^8\)，所以可以直接看作一定非零。

一个经典的应用是给出 \(n\) 阶矩阵 \(A,B,C\)，判断是否有 \(AB=C\)。

做法是随机一个向量 \(x\) 并判定模意义下 \(ABx=Cx\)。判断错 iff 对于非零矩阵 \(M=AB-C,Mx=0\)。
这里相当于是有 \(n\) 个 \(n\) 元一次多项式，每一个他等于零的概率都是 \(1/P\)，所以这个的错误率看似是 \(P^{-n}\)。
但是这 \(n\) 个随机事件他不独立，直接 xjb 放缩能拿到一个极松的上界 \(n/P\)。

行列式

快速过一下：

逆序对形式定义
余子式，Laplace 展开
高斯消元求行列式
积和式（NP）
\(\det A=\det A^T,\det(AB)=\det A\det B\)。

Cauthy-Binet Formula

\[\det(AB)=\sum_{S\in\binom{[n]}{m}}\det(A_{[m],S})\det(B_{S,[m]}) \]

（\([n]\) 表示集合 \([1,n]\cap\mathbb Z\)）

可以看作是行列式的一个组合意义：对于 \(m\times n\) 矩阵 \(A\)，\(n\times m\) 矩阵 \(B\)，得到的 \(m\times m\) 矩阵 \(AB\) 的行列式等于对应下标集合的【 \(A\) 的若干列、\(B\) 的若干行的行列式的乘积】求和。

例一

用线性代数知识判断一给定 n,n 二分图是否存在完美匹配。

根据定义，能发现完美匹配数量就是邻接矩阵（好像不能叫这个名字？）的积和式。

判定积和式非零，只需要给矩阵里所有非零位随机赋权求行列式，行列式为零则积和式几乎一定为零，错误率依然可以用 Schwartz–Zippel Lemma 捏出来。

例二

有点垃圾。跳了。

例三 LOJ 3409

两个小问。

mod 3 意义下，给 \(n\) 个 \(m\) 维向量，保证其张成空间 \(V\) 也是 \(m\) 维，从中选 \(m\) 个向量是 \(V\) 的一组基的方案数。
mod 2 意义下，给 \(n\) 个 \(m\) 维向量，每个向量有颜色，保证其张成空间 \(V\) 也是 \(m\) 维，每种颜色选一个向量、是 \(V\) 的一组基的方案数。