1.3 可压缩流:喷管和机翼
前言
劳张、劳江必看,劳高请随缘。
超音速喷嘴
基本
对于等熵流动,给出速度变化和管道截面面积变化的关系式:
对该公式分3种情况讨论:
- 低速、亚音速,M<1:此时\(M^2-1<0\),如果管道截面收缩(dA<0),流速将会增加(dV>0),若管道截面扩大,则流速下降。
- 音速,M=1:该处管道截面面积A为极小值。
- 超音速,M>1:管道截面扩大,流速上升。
这是因为,亚声速时密度变化比流速变化慢,而超声速时流速变化比密度慢。
因此,要想增加流速,应使得亚音速时管道截面面积收缩,超音速时扩大截面积。
为始终保持dV>0,构造一个先收缩后扩展的管道,中间为最小截面,即喉道(throat),这种形状的管道称为拉瓦尔喷管(De Laval nozzle)。
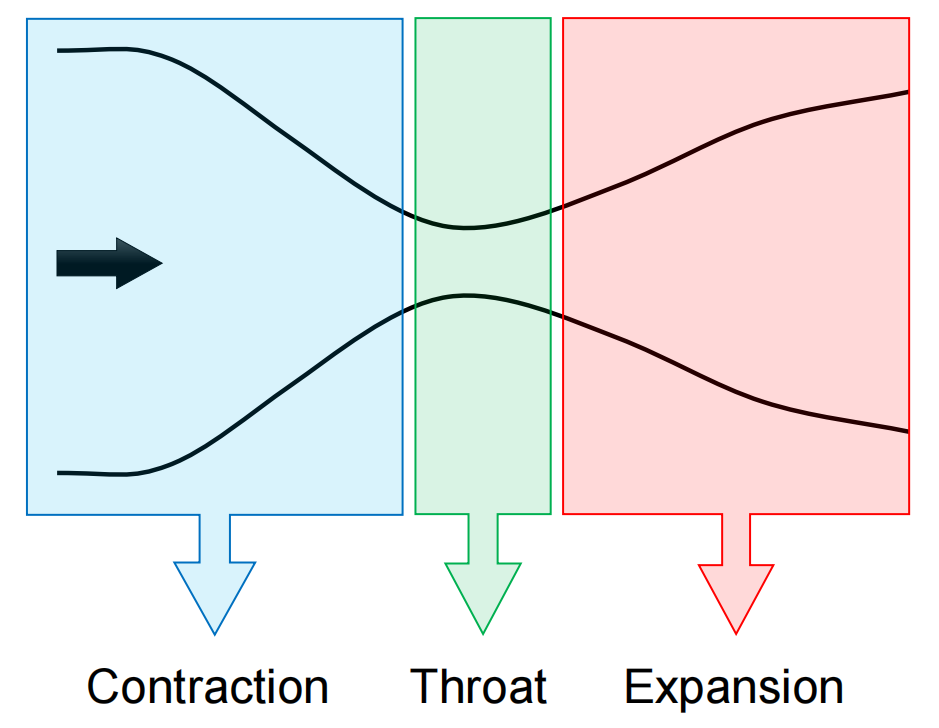
关于拉瓦尔喷管各段中的流动:
- 收缩(contraction):流动加速,在此定义初始条件。
- 喉部:用于阻塞(chock)流动,避免斜激波、膨胀扇产生
- 扩张:将流动加速到超音速。
另外需要注意的是,虽然拉瓦尔喷管内的流动,一般是绝能、不等熵流动,但在不出现激波时,或出现激波的波前、波后流动区域,仍然可以按绝能、等熵流动处理。
公式
对于几何参数已知的拉瓦尔喷管,其流动状态与特点,通常取决于喷管进口气流总压\(p_0^*\)、总温度\(T_0^*\)、喷管出口外界背压(即出口处的外界环境压力)\(p_b\)、喷管出口截面积和喉部截面积的比\(\frac{S_e}{S_t}\)。
接下来引入如下定义:
-
\[\begin{equation}\frac{S}{S_{t}}=\frac{1}{q(Ma)}=\frac{1}{Ma}\left[\left(1+\frac{k-1}{2}Ma^{2}\right)\left(\frac{2}{k+1}\right)\right]^{\frac{k+1}{2(k-1)}} \end{equation} \]
这里k=1.4(干燥空气),就是绝热指数\(\gamma\),只是换了个字母。
请和PPT中的公式对照,查看哪些变量被更换(公式效果是一模一样的):
\[\begin{equation}\frac{A}{A^*}=\frac{1}{M}\left[\frac{1+\frac{\gamma-1}{2}M^2}{\frac{\gamma+1}{2}}\right]^{\frac{\gamma+1}{2(\gamma-1)}} \end{equation} \] -
根据上述公式,可以绘制出如下图所示的图象:
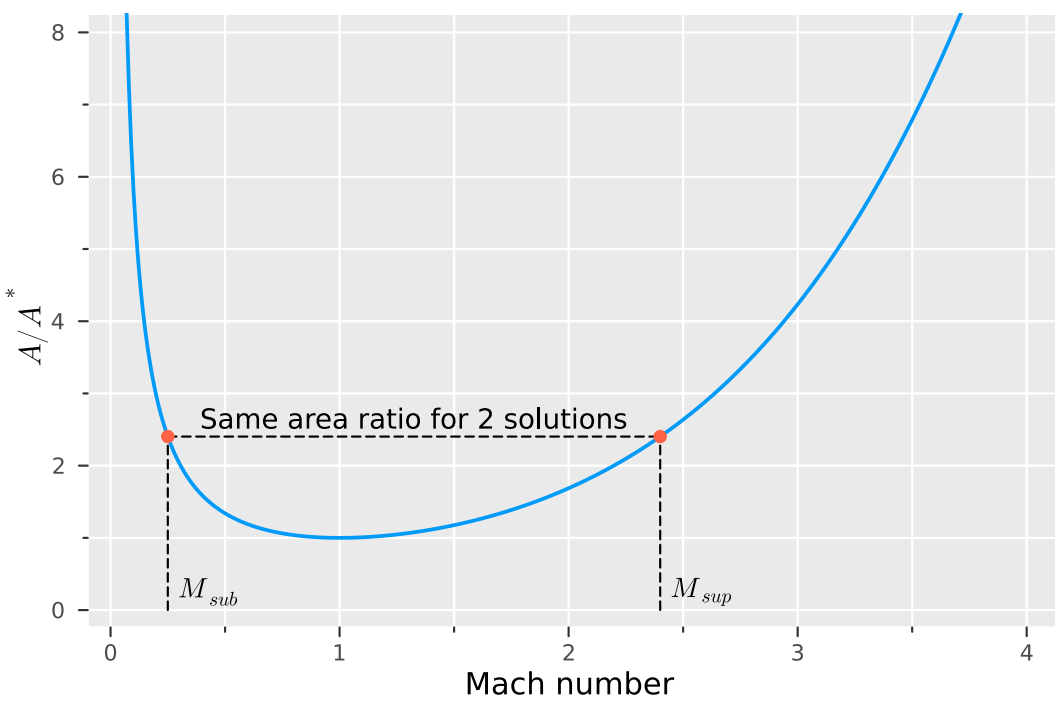
每个面积比均有两个马赫数与之对应,一个是亚声速的,一个是超声速的。
-
由于喷管出口截面马赫数\(Ma_e\)是和喷管进出口截面出的压强相比对应的:
\[\begin{equation}\frac{p_e^*}{p_e}=\left(1+\frac{k-1}{2}Ma_e^2\right)^{\frac{k}{k-1}}=f\left(\frac{S_e}{S_t}\right)=f\left(\frac{A}{A^*}\right) \end{equation} \]因此,一定的面积比(必要条件)、适当的压强比(充分条件),是拉瓦尔喷管出口截面处,得到指定马赫数的超音速气流的两个不可缺少的条件。
从这里开始,下面的许多推导和考试基本无关,赶时间的朋侑可以定性地快速阅读一下随着背压变化,拉瓦尔喷管扩张段及其下游的流动现象,然后直接跳转到“做题”小标题处。
上述截面积比的公式推导过程如下:


流动状态
下面就拉瓦尔喷管的几何特性、进口截面总压\(p_0^*\)、总温\(T_0^*\)一定时,喷管工作状态随着喷管下游外界背压\(p_b\)不同,发生变化的情况。
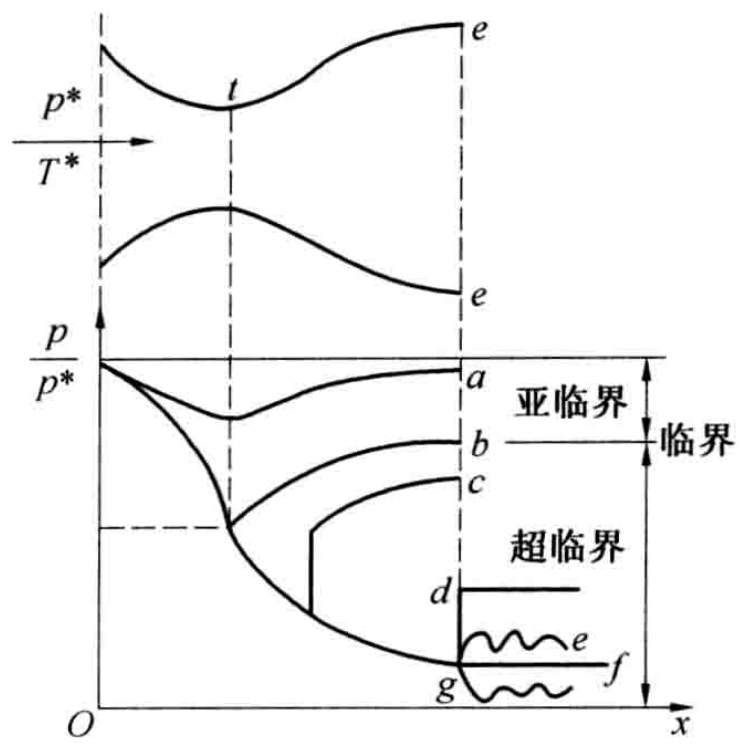
临界
对于一个确定的面积比,有两个马赫数对应,其中一个为亚声速。
这意味着,在一个恰当的背压或压强比下,亚音速气流在拉瓦尔喷管的收缩段加速,到喉部达到声速,此时马赫数为1;然后在扩张段减速,到出口处马赫数小于1,且喷管出口截面处的压力\(p_e\)等于背压\(p_b\)。气流静压沿喷管轴线的分布如上图曲线b所示。
此时流动的特点为:\(Ma_t = 1\),\(Ma_e < 1\),\(p_e = p_b\),气流在喷管内完全膨胀,喷管内无激波,管内流动可视为等熵。
定义此时的压强比:\(\frac{p_{\mathrm{b}}}{p_{\mathrm{e}}^{*}}=\frac{p_{\mathrm{m}}}{p_{\mathrm{e}}^{*}}\),其中\(p_m\)是临界状态下的喷管出口截面压强。
亚临界
劳张必看
在临界状态下,喷管出口背压的微小扰动,可以在扩张段内,以声速逆流传播。
如果背压增加,意味着通过喉部的最大流量,不可能在喷管出口处流出,即出现“阻塞”现象。
于是,喉部处马赫数变成\(Ma_t < 1\)以维持能量守恒,整个喷管内均为亚音速流动,相当于扰动“越过”声速线,进而影响整个喷管内的流动。
在亚临界状态下,拉瓦尔喷管内的流动全部为亚音速。
考虑极限情况:当\(\frac{p_{\mathrm{e}}}{p_{\mathrm{e}}^{*}}=\frac{p_{\mathrm{b}}}{p_{\mathrm{e}}^{*}}=1\)时,整个喷管内没有流动,静压=总压,且沿着喷管轴线不变,如上图中亚临界范围最上边的线所示。
当\(\frac{p_\mathrm{m}}{p_\mathrm{e}^*}<\frac{p_\mathrm{b}}{p_\mathrm{e}^*}<1\)时,即此时的喷管出口下游外界背压略高于临界状态的喷管出口截面压强,气流在收缩段加速,到喉部仍然为亚音速,之后在扩张段减速,到出口处\(Ma_e<1\),\(p_e = p_b\),如图中曲线a所示。
特别注意:
- 与没有流动的情况相比,亚临界流动状态下,气流具有一定的速度,因此具有动压。
- 根据能量守恒,对于绝热流动,总焓 (静焓 + 动能) 保持不变。由于总焓与总压有直接关系,总焓不变可以近似理解为总压不变(更严谨地说,总压在等熵流动中不变,在非等熵流动中会改变)。
- 由于亚临界流动下存在动压,而总压近似不变(或者说,与无流动情况相比,总压即使有微小改变也是由于流动建立初期的微弱激波/压缩波造成的,我们可以暂时忽略),那么静压必然会比没有流动时低。
注意:这种流动状态下,气流在喷管内完全膨胀。
超临界
物理原理
当背压下降时,由于管内流量不能超过最大流量,还要求气流压力逐渐下降等于背压,因此只有在喉部之后的扩张段,出现超音速流动,增速、减压,才能满足上述要求,因为亚音速流动在扩张段减速增压。
通过截面面积的增加、\(q(\lambda)\)(上面手工验证公式中给了定义式,它叫流量函数,表示单位时间内通过单位面积的质量流量,是无量纲的密流)减小,维持管内最大流量不变,之后的降压扰动不会逆流穿过流场的超音速区。
但是,考虑到压强比、马赫数、面积比三者之间存在对应关系,假设背压下降一个小量,气流通过喉部之后,只需要通过很短的扩张段内超音速流动就能达到背压要求。
此时,超音速气流进一步经过一段加速、降压流动,压力比背压低一些,使得喷管内某处出现一道正激波,使得气流压强增大、变为亚音速流动,亚音速流在激波后的扩张段减速、增压运动,直到出口截面处和背压一致。
若背压下降再多一些,激波后压力下降,激波逆流传递速度减小,喷管后的激波降顺流向后,移动到一个新的稳定位置。
背压持续下降,激波将逐渐后移到喷管出口截面处,甚至转变为斜激波,使管内流动变成等熵的。
当压强比下降到与出口截面马赫数\(Ma_e\)之间的关系符合式4时,激波消失。
若背压继续下降,喷管出口后将出现膨胀波系,让超音速气流加速、降压到和\(p_b\)相当。
流动状态
当\(\frac{p_\mathrm{m}}{p_\mathrm{e}^*}>\frac{p_\mathrm{b}}{p_\mathrm{e}^*}\)时,气流在收缩段加速,到喉部\(Ma_t = 1\),然后在扩张段内的流动,根据\(\frac{p_b}{p_e^*}\)大小不同,分4种情况讨论。
1 设计状态
气流在扩张段内继续加速,到出口处\(Ma_e > 1\),并达到完全膨胀状态,\(p_e = p_b\),整个扩张段内无激波、出口外无激波/膨胀波,如图中曲线f所示。
记该状态下,出口截面压强为\(p_I\),压强比\(\frac{p_{\mathrm{b}}}{p_{\mathrm{e}}^{*}}=\frac{p_{\mathrm{l}}}{p_{\mathrm{e}}^{*}}\)。
此时,\(Ma_1=1,~Ma_\mathrm{e}>1,~p_\mathrm{e}=p_\mathrm{l}=p_\mathrm{b},~\dot{m}=\dot{m}_{max}\)。
2 不完全膨胀,有管外膨胀波束
若压强比\(\frac{p_{\mathrm{b}}}{p_{\mathrm{e}}^{*}}<\frac{p_{\mathrm{l}}}{p_{\mathrm{e}}^{*}}\),这种压力扰动不能逆流影响喷管出口截面、管内流动,因此喷管内的流动和设计状态一样,有\(p_\mathrm{e}=p_I>p_\mathrm{b}\),气流在喷管内没有得到完全膨胀。
因此,超音速气流将在喷管出口,往下游产生膨胀波束,如曲线g所示。
此时,\(Ma_1=1,~Ma_\mathrm{e}>1,~p_\mathrm{e}=p_\mathrm{l}>p_\mathrm{b},~\dot{m}=\dot{m}_{max}\)。
3 过膨胀,有管外/管口激波
此时压强比\(\frac{p_{\mathrm{b}}}{p_{\mathrm{e}}^{*}}>\frac{p_{1}}{p_{\mathrm{e}}^{*}}\),背压大于喷管出口压强\(p_e = p_I\),气流将在出口产生斜激波,以提高压力到\(p_b\),其强度由激波前后压强比确定,如图中曲线e所示。
随着压强比增加(背压增加),激波不断增强、激波角逐渐增大,而当\(\beta = 90^{\circ}\)时,斜激波变成紧贴在喷管出口截面的一道正激波,如图中曲线d所示。
注意,这种状态下,背压变化不会影响喷管内流动和气流参数计算方法,因此气流参数说明公式同状态2,不完全膨胀。
定义此时的外界背压为\(p_{II}\),压强比:
4 过膨胀,管内正激波
背压进一步增大,\(\frac{p_{\mathrm{b}}}{p_{\mathrm{e}}^{*}}>\frac{p_{\mathrm{ll}}}{p_{\mathrm{e}}^{*}}\),随着压强比增加,正激波前后压强比增加,激波的逆流传播速度加大,正激波逐渐向喷管内移动。
随着逆流与出口截面的距离增大,喷管扩张段内的超声速气流压力更高、马赫数更小,波前压力增加,激波强度及其逆流传播速度下降。
因此,当激波移动到某个位置,传播速度等于超声速气流的速度,激波会稳定在这个位置。图中曲线c所示。
此时,喉部\(Ma_t = 1\),出口处\(Ma_e < 1\),\(p_e = p_b\),\(\dot{m} = \dot{m}_{max}\)。
若压强比继续增加,激波越接近喷管喉部,波前压力越高、激波强度越弱;
当激波恰移动到喉部时,波前马赫数为1,激波不存在,即临界状态。
下面列出喷管内激波位置计算方程,劳江可以看看,推导过程我也不会,没整理。
令\(S_S\)表示激波所处的截面积。
应该是用的一维定常流动的质量守恒,我手写笔记里有,然后进一步代入公式往下写的。
接下来先补充一下手写笔记缺失的气动函数定义部分,再往下写。
有\(y(\lambda_{\mathrm{e}})=\frac{p_{0}^{*}}{p_{\mathrm{b}}}\frac{S_{\mathrm{t}}}{S_{\mathrm{e}}}\),查表/计算出\(\lambda_e\)或者\(Ma_e\),再用一次质量守恒:
计算得激波总压恢复系数:
即激波后总压/激波前总压。
查表或计算得\(Ma_S\)。
由于喉部到激波所处位置之前,超声速流动区域内,流动是绝能等熵的,故有:
做题?
接下来直接开始讲做题中的不同假设和公式。
-
若流动是等熵的,即管内没有激波(包含除过膨胀-管口/管内正激波以外的所有情况):
直接用等熵可压缩流动关系方程就是了,1.1有详细阐述。
对于一个给定的拉瓦尔喷管,存在一个“设计状态”或“理想超音速膨胀”状态,出口截面的流动恰好达到超音速,且出口压力等于环境压力。
直接找这个设计点:考虑\(\frac{p^{*}}{p_{0}}\leq0.528\),对于给定的或要求的\(\frac{A_e}{A^*}\),计算出口马赫数\(M_e\)即可。
-
若管内流动不是等熵的,即过膨胀-管内/管口正激波:
需要用正激波的物理量关系,此事在1.2笔记中亦有记载。
在极限情况下(过膨胀-管口正激波),利用上游的“设计条件”对喷管进行评估(检查 )。
-
使用如下计算马赫数。
\[\begin{equation}\frac{A}{A^*}=\frac{1}{M}\left[\frac{1+\frac{\gamma-1}{2}M^2}{\frac{\gamma+1}{2}}\right]^{\frac{\gamma+1}{2(\gamma-1)}} \end{equation} \] -
当喉部阻塞,我们达到了最大质量流量:
\[\begin{equation}\dot{m}_{max}=\rho^*u^*A^*=\rho^*a^*A^* \end{equation} \]
下一步,讨论过膨胀-管内正激波情况下,求解流动参数的迭代步骤:
- 利用式4/11,即面积比方程,已知入口面积、喉部面积,求入口马赫数
- 已知入口马赫数、静参数(压强、温度、密度),利用等熵关系计算总静压、总静温、总密度
- 假设激波位于某个截面\(A_G\),利用面积比方程,并已知\(A_G/A^*\),计算得激波前超音速马赫数
- 利用正激波关系式,计算激波后马赫数、静压、静温、密度
- 根据激波后总参数,和出口面积,利用面积比方程,计算出口马赫数
- 根据出口马赫数、激波后总压,利用等熵关系,计算出口静压,并和外界背压比较。
- 若计算得的出口静压和边界条件不一致,则调整假设的激波位置,重复步3-6,知道计算得到的\(p_e\)和边界条件匹配。
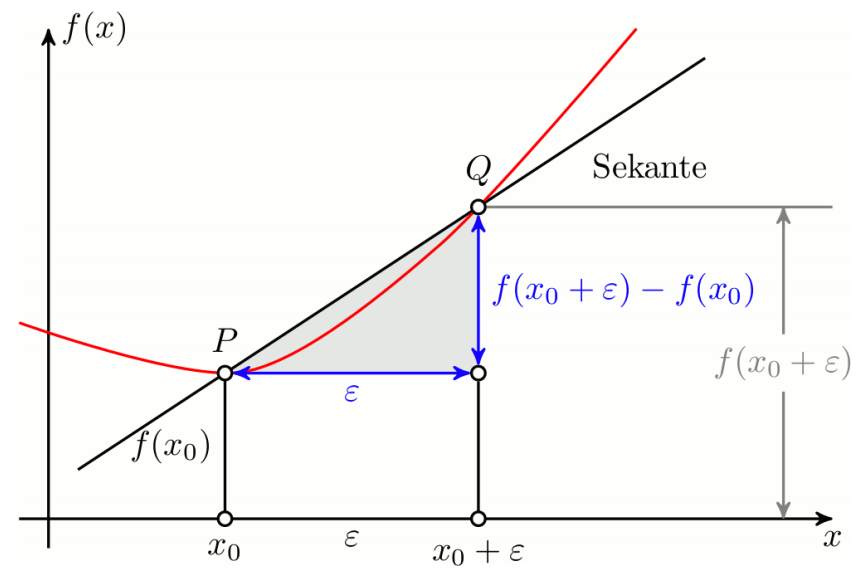
至于迭代方法,牛顿-拉夫森法、割线法等均可,这里直接给出割线法(secant method)的公式:
超音速进气道
基本
飞机做超音速飞行时,相对于飞机,气流也是以超音速流向飞机的。
但发动机的进口需要亚音速气流,因此需要使用超音速进气道,把超音速气流减速为亚音速气流,同时尽量少产生损失、不均匀度。
可以直接让超音速气流经历一道正激波,减速成亚音速气流,但总压损失较大。
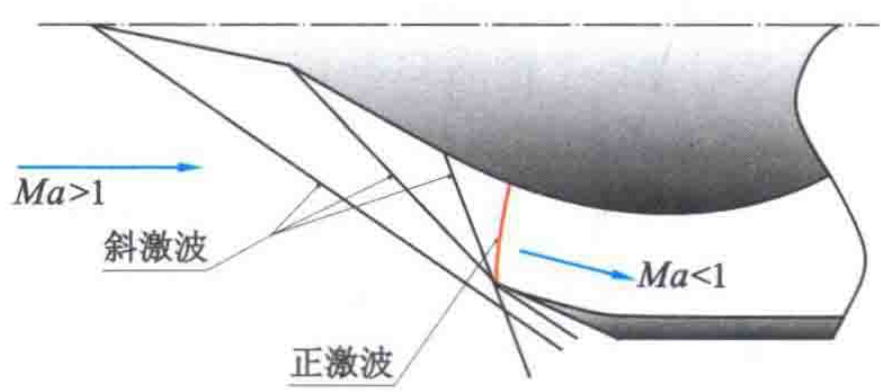
如图,我们先让超音速气流经过一系列斜激波,逐渐减速,最后再经过一道强度大大减弱的正激波,减速成亚音速气流,这样做的总压损失要小得多。
类型
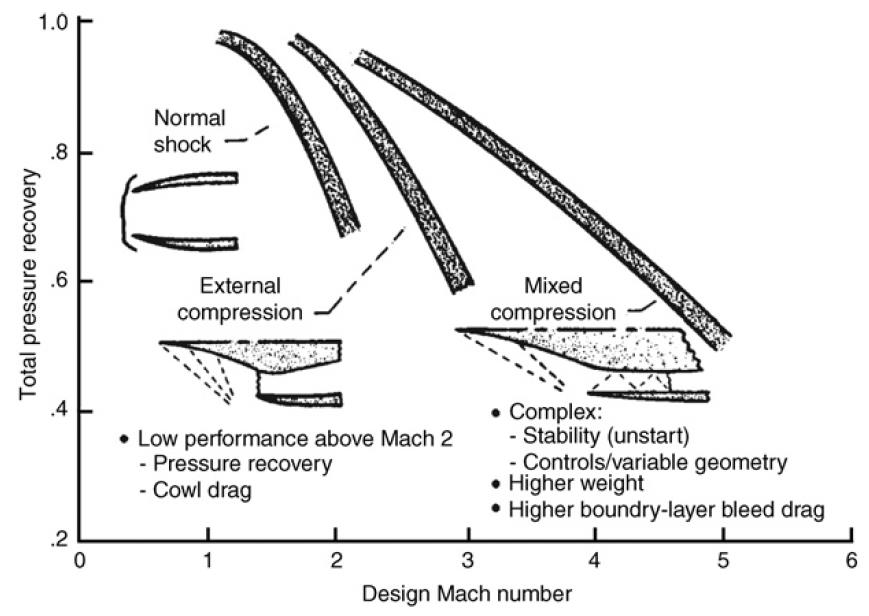
根据设计状态下,超音速气流滞止过程的特点,把超音速进气道分为外压式、内压式、混压式。
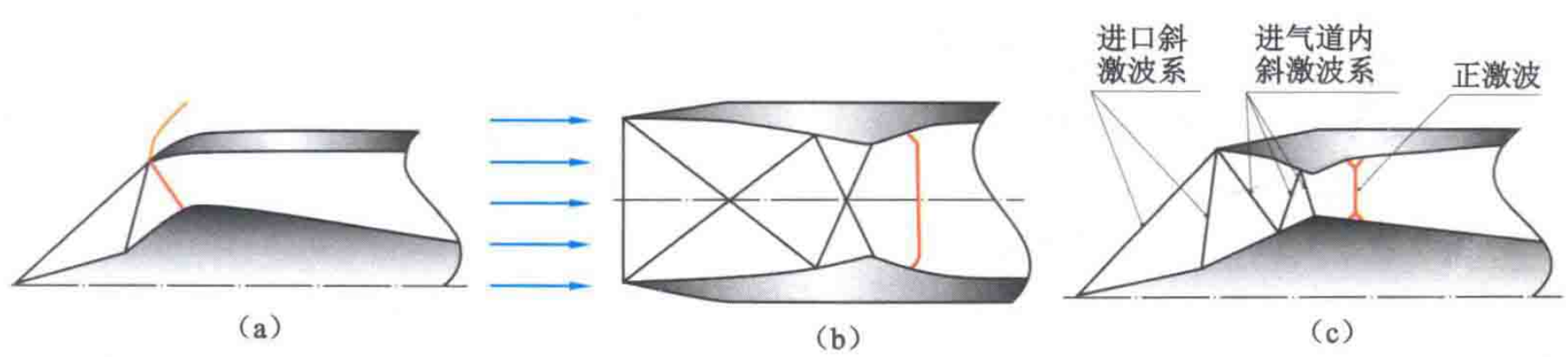
- a:外压式,在进口之前把超音速气流滞止到亚音速,总压恢复系数在马赫数2及以下表现较好;
- b:内压式,超音速气流的减速、增压过程完全在进口内进行;
- c:混压式:超音速气流一部分在进口以外减速扩压。一部分在进口以内减速扩压,总压恢复系数可以在更高的马赫数下维持较高,但结构更复杂。
三种进气道随着马赫数增加的总压恢复系数(\(\sigma_{\mathrm{i}}=\frac{p_{1}^{*}}{p_{0}^{*}}\),进气道出口气流总压\(p_1^*\)和未受扰动气流的总压\(p_0^*\)的比例)和特性如下图所示。
内压式进气道的起动问题
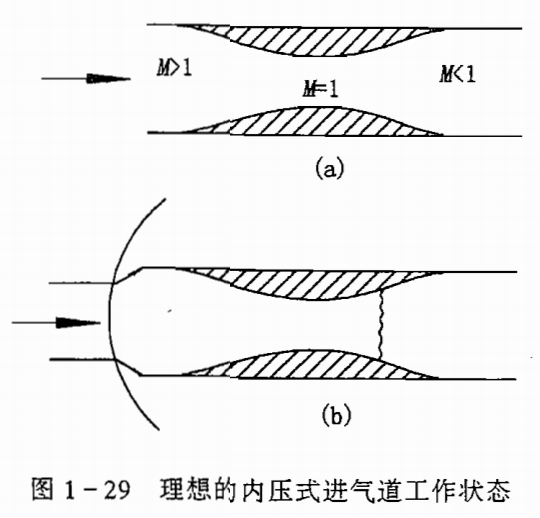
上图a展示的是理想的内压式进气道工作状态,超音速来流直接流入进口,在收缩段减速,到喉道处到达声速,在扩张段内变成亚音速,像一个倒过来的拉瓦尔喷管(只是来流速度变了)。
可建立喉道截面积和进口捕获面积之间的关系:
然而,在内压式进气道的不起动工作状态,进口前会有一道脱体激波,从该激波到喉道前是亚音速流,喉道处到达音速,喉道处为超音速,并在喉道下游某处形成一道正激波。
这里对脱体激波的形成机制做详细说明:
-
低马赫数来流下,进气道难以启动的根本原因在于其为超音速设计的几何形状不再适用。
根据等熵关系式1,在低速来流下,这种进气道对来流起加速作用,而不是像高马赫数超音速那样减速,进气道内部难以建立有效的压缩过程,无法在进气道内恰当地将流动与下游发动机衔接;
同时,发动机低需求、压气机低效率和燃烧室压力等因素导致的高背压进一步提高了启动所需的压力比,加剧了启动难度。
-
由于进气道在低马赫数下无法在内部进行充分的、有效的连续压缩,且进气道下游的高背压成分持续向上游传播,使得进气道内部和外部的压力无法连续。
因此,气流无法平滑地“贴合”进气道外壁进入内部,必须在入口前方形成脱体激波,通过激波后的压力跃升来迅速抬高流动压力,以满足内外压力连续的条件。
-
高背压将脱体激波“推”到进气道外部。
脱体激波的产生是以牺牲外部来流品质(产生激波损失、流动分离)为代价的,其好处是能够让进气道内部在一定程度上维持相对较高的压力,以匹配发动机的需求。
-
即使在\(\frac{A_{throat}}{A_{inlet}}\)较大的情况下,由于低马赫数来流的限制,进气道也难以启动。
对于给定的入口马赫数,\(\frac{A_{throat}}{A_{inlet}}\)越大,进气道在启动过程中需要吞入的空气流量越大,虽然这在一定程度上更有利于克服背压将激波吞入,但这也不是进气道能否起动的决定性因素。
这样的问题是,气流经过两道激波,会造成很大的总压损失。
使内压式进气道从不起动状态变成起动,也就是把进口前的脱体激波吸入到进口内,建立起正常工作状态的过程,称为起动过程。
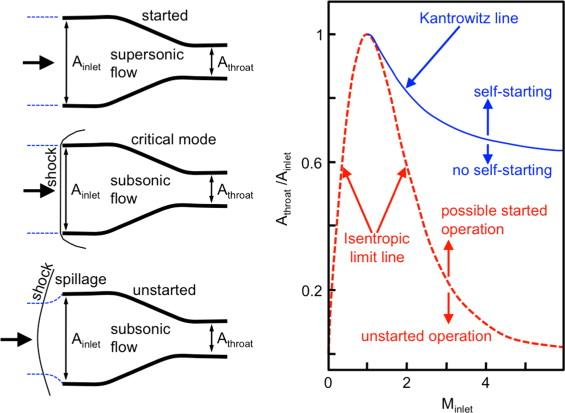
随着来流马赫数增大,进气道内外压力失配减少,脱体激波会向机体表面靠拢。
当满足一定“自启动”条件(如 Kantrowitz limit),进气道就会从外部脱体激波过渡到内部斜激波或正激波组合。
这样,进气道内部获得设计所需的多次激波压缩,流动效率与总压恢复度显著提高。
为实现该过程,可以直接增加来流速度,先超过设计马赫数,再退回到设计速度。
但这对风洞好说,对飞机就不那么好做到了。
所以,要不就把喉道面积增大,把口外的脱体正激波消除:
这里\(\sigma_{\mathrm{I}_0}\)是正激波前的马赫数是自由流马赫数时的激波总压恢复系数,乘以0.98是考虑附面层对喉道面积的减小。
或者采用不连续的楔面/锥面,设计成分级压缩系统,让气流马赫数在管道内,减小到适合结尾正激波的低马赫数(此时应考虑斜激波反射):
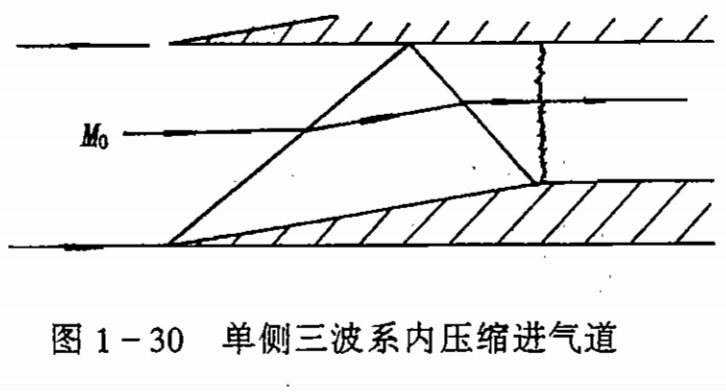
但无论如何,这个启动问题始终是存在的。
外压式进气道的正激波位置
目前,常用的是外压式进气道,即用一系列在进气道外的斜激波+一道进气口处的正激波减速。
接下来考虑外压式进气道的三种不同工况。
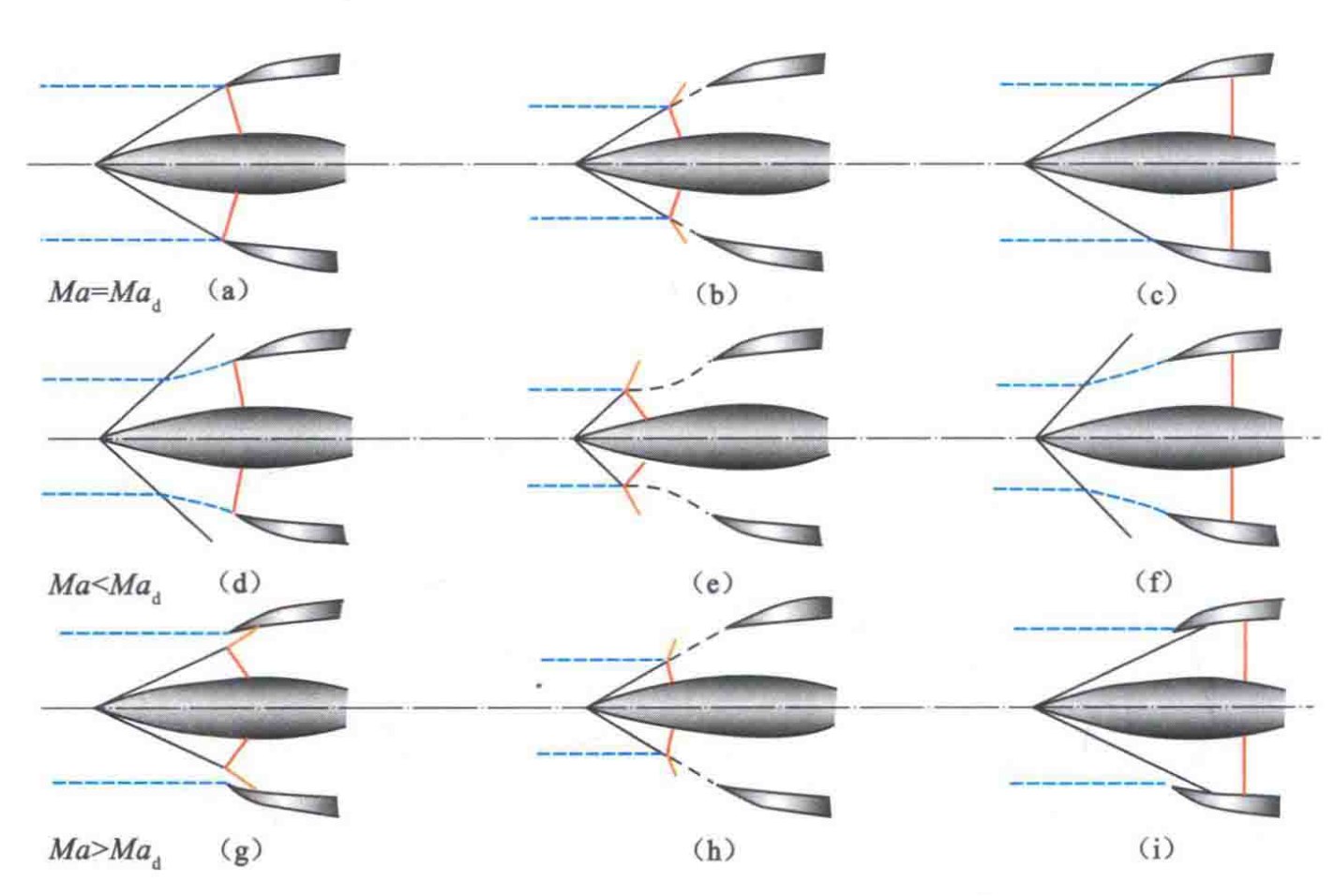
临界
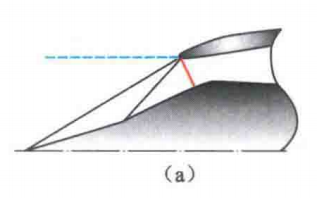
结尾正激波处于进气道唇口处的流动状态,称为进气道的临界工作状态。
如上大图左侧部分的三个进气道。
此时,总压损失小、没有溢流,因此没有附加阻力,外罩阻力较小。
超临界
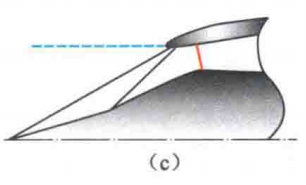
当发动机需要的气量增大、出口流通能力增大,则反压下降较多,正激波会被吸入进气道的扩散通道里。
斜激波后的超音速气流,在扩散通道内继续加速,通过一个较强的正激波,转为亚音速气流。
此时,正激波前马赫数增大,总压损失增加。
如果后移过多,还可能引起激波和进气道壁面边界层的干扰,引起气流分离,使得总压损失急剧加大,进气道性能恶化。
如上大图右侧的进气道。
亚临界
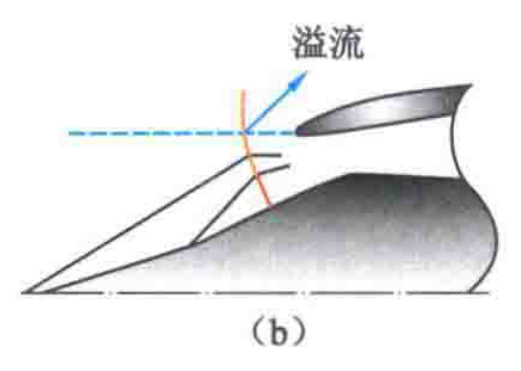
在临界工作状态基础上,减小出口的流动能力:发动机转速减小、大气温度升高、飞行马赫数增加,导致发动机需气量减小。
这样,正激波后的反压升高,把正激波推离进口端面位置,向前移动,和斜激波交于进口前,形成三叉激波。
这会引起溢流,波后气流参数不均匀,会有滑流层进入进气道,使得气流总压损失增大,外罩阻力增加。
如上大图中间所示。
严重时(超音速飞行、深度亚临界),会使得进气道进入不稳定状态,即进气道的喘振:正激波在进气道进口内外,迅速往返移动,气流总压呈现低频、大幅度脉动,空气流量忽大忽小的波动,飞行员可听到机头前发出强烈爆声,感到周期性推力脉动。
这会诱发风扇、压气机的喘振、加力熄火,发动机熄火,而且在很大的交变载荷作用下,可能导致飞机、发动机结构破坏。总之是绝对不允许发生的。
超音速机翼
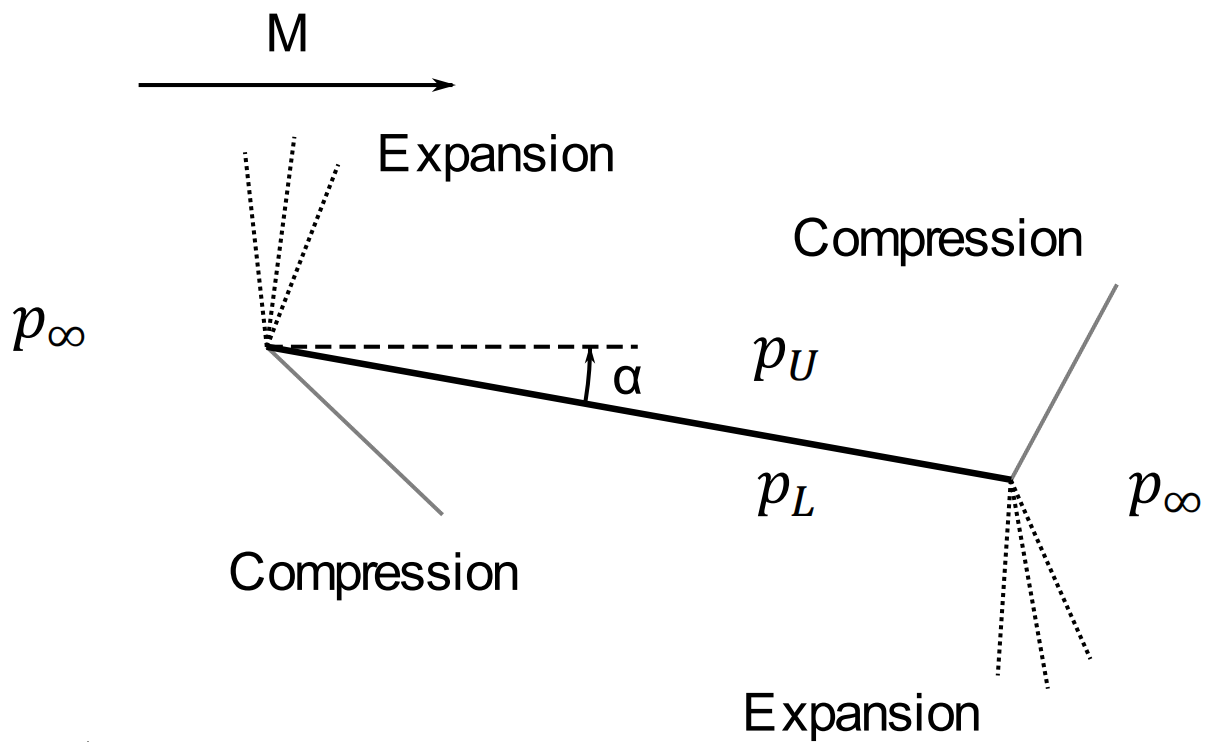
对于如上图所示,超音速、迎角较大的情况,在机翼前缘的上面,空气膨胀,产生膨胀波;在前缘下面,空气受强烈阻滞,产生激波。
在机翼后缘,上表面气流相当于流过内折角,受阻滞减速,产生激波;下表面的气流相当于流过外凸角,膨胀加速,产生膨胀波。
-
求前缘上表面膨胀波压强比:
\[\begin{equation}\frac{p_U}{p_\infty}=\frac{p_U}{p_0}\frac{p_0}{p_\infty} \end{equation} \]这里,引入了来流总压\(p_0\)作为中间变量,\(\frac{p_U}{p_0}\)通过等熵关系+\(M_U\)得到,\(\frac{p_0}{p_\infty}\)通过等熵关系+来流马赫数M得到。
已知外折角\(\theta\)(等于图中\(\alpha\))、\(M_1\)(来流马赫数M),套用普朗特-迈耶尔流动公式,可求出\(M_2 = M_U\)。
-
求前缘下表面斜激波压强比:
\[\begin{equation}\frac{p_{L}}{p_{\infty}}=\frac{2\gamma M_{n,\infty}^{2}-(\gamma-1)}{\gamma+1} \end{equation} \]这里,为了知道流动马赫数的斜激波法向分量\(M_{n,\infty}\),只需结合\(\theta - \beta - M\)关系图,或用数值迭代方法得到激波角\(\beta\),然后使用\(M_{n,\infty}=M_{\infty}\sin(\beta)\)即可。
-
求升力、阻力系数:

-
升力:(\(F_L\)和\(F_U\)是黑色线)
\[\begin{equation}L=(F_L-F_U)\times\cos(\alpha) \end{equation} \]\[\begin{equation}C_l=\frac{L}{0.5\rho V^2S}=\frac{L}{0.5\gamma p_\infty M_\infty^2S} \end{equation} \] -
阻力:
\[\begin{equation}D=(F_L-F_U)\times\sin(\alpha) \end{equation} \]\[\begin{equation}C_d=\frac{D}{0.5\rho V^2S}=\frac{D}{0.5\gamma p_\infty M_\infty^2S} \end{equation} \]
-