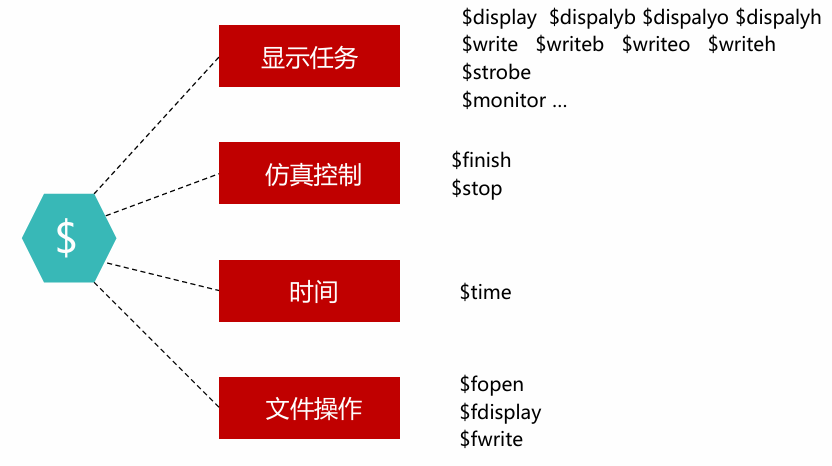
试除法
从 \(2\) 枚举到 \(\lfloor\sqrt n\rfloor\) 判断能否整除。
朴素筛法
从小到大枚举每个数,将范围内它的倍数全部标记为合数。
时间复杂度显然就是调和级数 \(O(n\log n)\)。
埃氏筛
观察到一个合数必定可以通过某个质数乘上某个数得到。
从小到大枚举每个质数,将范围内它的倍数全部标记为合数。
有一个小优化,对于 \(p\) 这个质数,枚举 \(i\) 筛掉 \(p\times i\) 时我们强制钦定 \(p\leq i\),因为 \(p>i\) 的情况肯定在 \(i\) 中至少一个质因子那里筛过了。
时间复杂度 \(O(n\log\log n)\),证明不在考察范围内。
欧拉筛
发现埃氏筛中的小优化只是去除了一部分重复的情况,我们希望一个合数只在它最小的质因数那里被筛一次。
先枚举 \(p\) 再标记不好处理,不妨先枚举 \(i\),再去考虑哪些 \(p\) 是无用的。
发现如果 \(p\times i\) 被一个比 \(p\) 更小的质数 \(q\) 筛去了,那么其实就是 \(q|i\)。
所以在枚举 \(p\) 的过程中,一旦发现 \(p|i\) 直接退出即可,\(i\) 乘更大质数的合数肯定会被 \(p\) 筛掉。
时间复杂度 \(O(n)\)。