动态规划—兑换零钱（一）解析+代码

兑换零钱（一）

题目链接：兑换零钱（一）

题目描述：

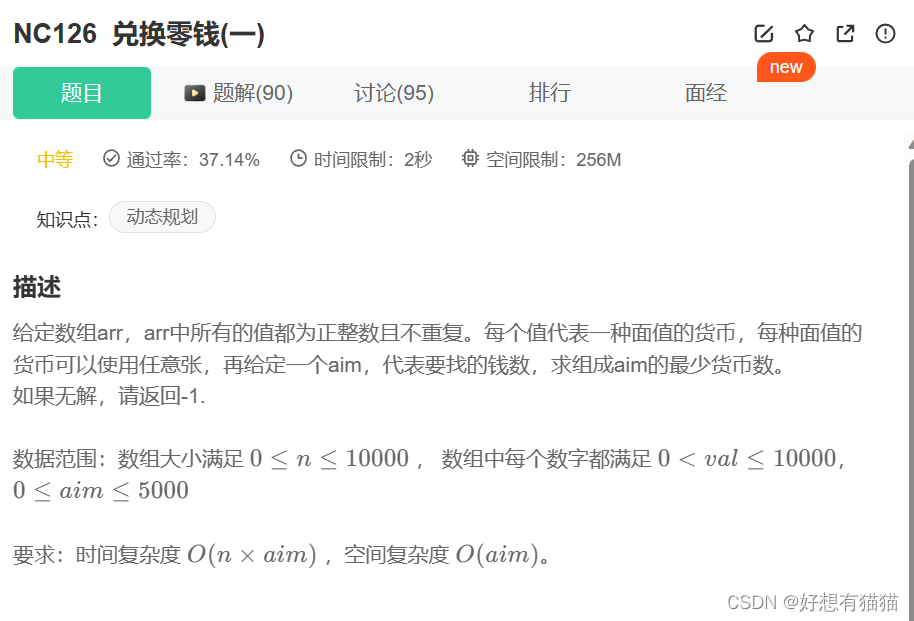
在这里插入图片描述

题目既要求要刚好组成该钱数，又要求是组成该钱数的最少货币数。
面对不同面额的零钱，我们无法直接确定其所需数量，也不知道如何组成最少。
那么我们可以采用问题缩小，缩小成钱数-1，钱数-2 … … 1，组成该钱数的最少货币数

所以我们使用动态规划的思想。将钱数分成1块1块，然后保存组成每一部分钱数的货币数，最终递推到目标钱数

初始状态
因为所求是最少货币数，我们使用一维数组即可。而数组存储的就是组成当前钱数的最少货币数。
因为最后取最小，而100块最多由100个1块组成，所以一维数组的初始化为目标钱数即可。
状态转移方程
dp[ ]内存储的是组成当前钱数的最少货币数，对于一个面额的零钱，我们有两种选择：
1 不使用该零钱：dp[ i ] = dp[ i ]
2 使用该零钱：如果使用，那么相当于当前钱数 - 该面额零钱 +1 ，假如当前是arr（零钱数组）的第 j 个面额
dp[ i ] = dp[ i - arr[ j ] ] + 1
因为要取最小，所以dp[ i ] = min( dp[ i ] ，dp[ i - arr[ j ] ] + 1 )

代码如下：

int minMoney(vector<int>& arr, int aim){//将aim分解成每一个1块钱//状态表示凑到当前钱数的最少货币数//aim最多由aim个1元组成，所以数组大小定为aim+1，每个数组数据也设为aim+1，方便取最小值vector<int>dp(aim+1,aim+1);dp[0]=0;//将aim分解成1块1块for(int i=1;i<=aim;++i){//遍历所有面额的货币for(int j=0;j<arr.size();++j){//可以凑到当前钱数if(arr[j]<=i){//取最小//当前货币数和使用该面额货币+1的货币数dp[i]=min(dp[i],dp[i-arr[j]]+1);}}}return dp[aim]>aim?-1:dp[aim];}