组合逻辑电路的分析

组合逻辑电路：任何时刻电路的输出状态只取决于该时刻的输入状态，而与该时刻以前的电路状态无关。

组合逻辑电路的分析

分析步骤

1. 由逻辑图写出输出端的逻辑表达式
2. 运用逻辑代数化简或变换
3. 列逻辑状态表
4. 分析逻辑功能

例题1

分析下图的逻辑功能

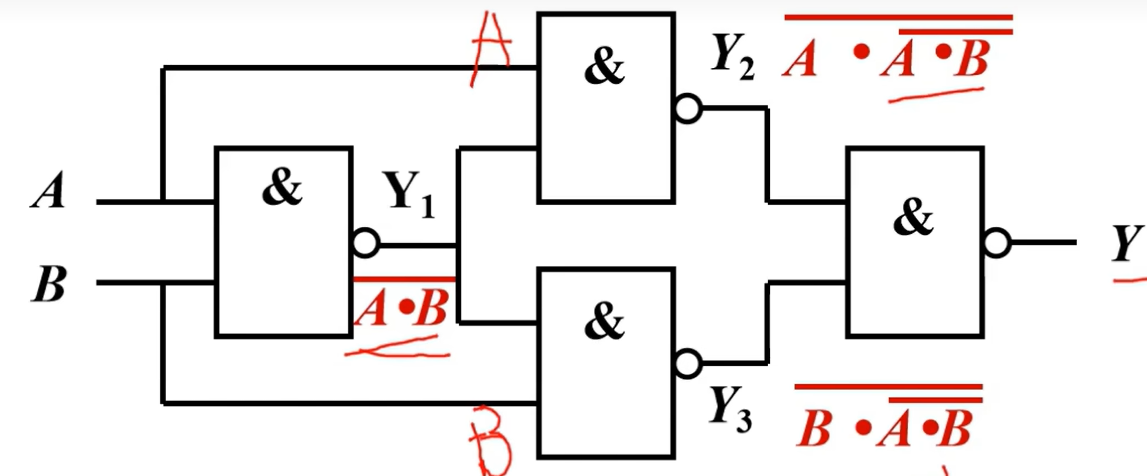
1. 写出逻辑表达式

\[Y=\overline{Y_{2}\:Y_{3}}\:=\overline{\overline{A\cdot\overline{AB}}+\overline{B\cdot\overline{AB}}} \]

2. 应用逻辑电路化简

\[\begin{aligned} \mathrm{Y} & =\overline{\overline{A\cdot\overline{AB}}+\overline{B\cdot\overline{AB}}} \\ & =\overline{\overline{A\cdot\overline{AB}}+\overline{B\cdot\overline{AB}}} \\& =A\cdot\overline{AB}+B\cdot A\overline{B} \\& =A\cdot(\overline{A}+\overline{B})+B\cdot(\overline{A}+\overline{B}) \\& =A\overline{B}+\overline{A}B \end{aligned}\]

3. 列逻辑状态表

A	B	Y
0	0	0
0	1	1
1	0	1
1	1	0

4. 分析逻辑功能
   该电路的功能是当A和B不同时，Y=1，否则Y=0。所以，该电路是异或门。

例题2

分析下图的逻辑功能

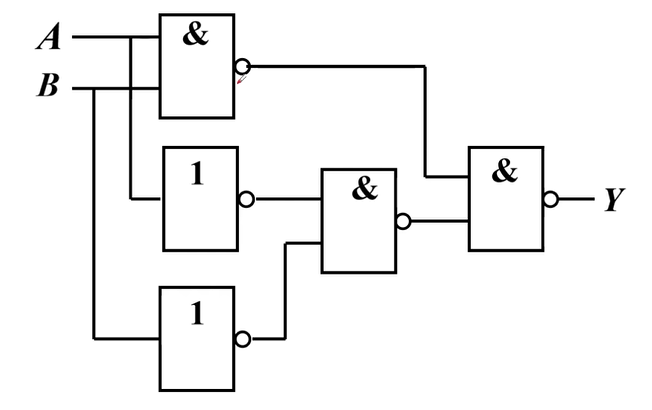
组合逻辑电路的设计

设计步骤

1. 由逻辑要求，列出逻辑状态表
2. 由逻辑状态表写出逻辑表达式
3. 简化和变换逻辑表达式
4. 画出逻辑图

例题3

设计一个三人(A、B、C)表决电路。每人有按键，如果赞同，按键，表示“1”;如不赞同，不按键，表示“0”。表决结果用指示灯表示，多数赞同，灯亮为“1”，反之灯不亮为“0”。

1. 列出逻辑状态表

A	B	C	Y
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

2. 写出逻辑表达式

\[\begin{aligned} \mathrm{Y} & =\overline{A\cdot B\cdot C}+\overline{A\cdot B\cdot\overline{C}}+\overline{A\cdot\overline{B}\cdot C}+\overline{\overline{A}\cdot B\cdot C} \\ & =\overline{A\cdot B}+\overline{A\cdot C}+\overline{B\cdot C} \end{aligned}\]

3. 用与非门构成逻辑电路

\[Y = \overline{A\cdot B}+\overline{A\cdot C}+\overline{B\cdot C} = \overline{\overline{AB}\cdot \overline{BC}\cdot\overline{AC}} \]

4. 画出逻辑图

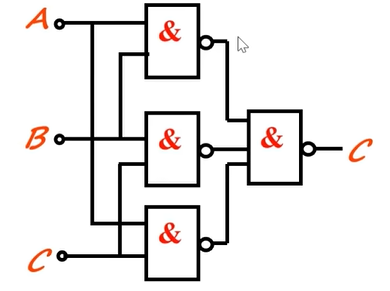
例题4

设计一个三变量奇偶检验器，要求:当输入变量A、B、C中有奇数个同时为“1”时，输出为“1”，否则为“0”。用“与非”门实现。

1. 列出逻辑状态表

A	B	C	Y
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

2. 写出逻辑表达式

\[\begin{aligned}= \mathrm{Y} & =\overline{AB}C+\overline{A }B\overline{C}+A\overline{BC}+ABC \\ \end{aligned}\]

3. 用与非门构成逻辑电路

\[Y = \overline{AB}C+\overline{A }B\overline{C}+A\overline{BC}+ABC = \overline{\overline{\overline{AB}C}\cdot\overline{\overline{A }B\overline{C}}\cdot \overline{A\overline{BC}}\cdot \overline{ABC}} \]

4. 画出逻辑图

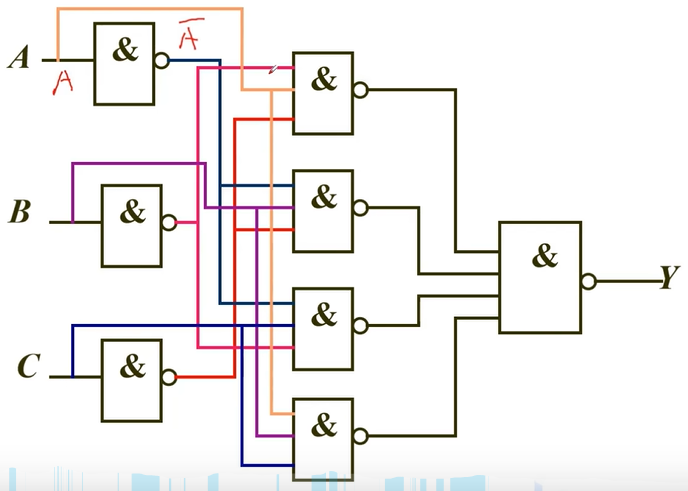
例题5

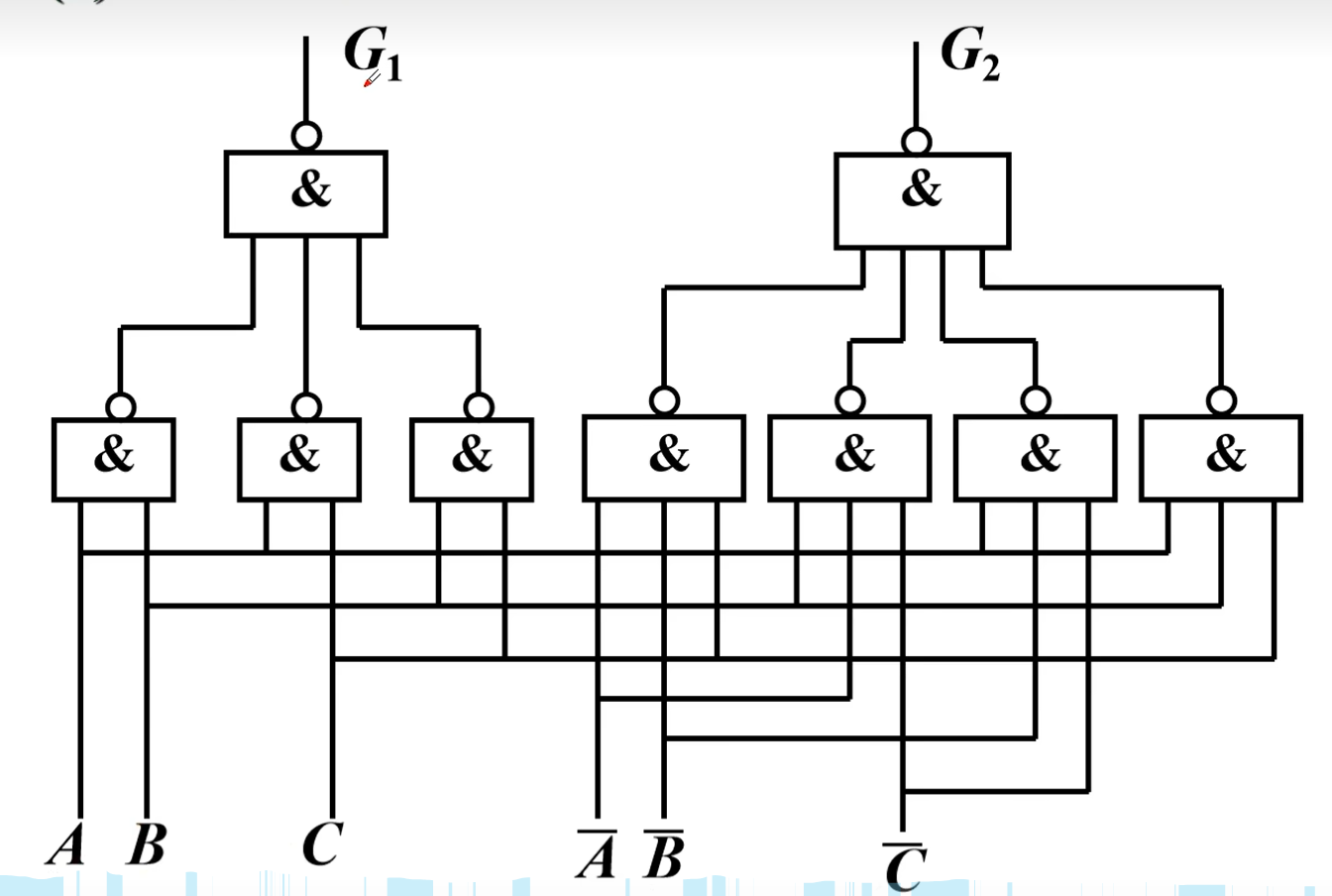
某工厂有A、B、C三个车间和一个自备电站，站内有两台发电机G1和G2。G1的容量是G2的两倍。如果一个车间开工，只需G2运行即可满足要求;如果两个车间开工，只需G1运行，如果三个车间同时开工，则G1和G2,均需运行。试画出控制G1和 G2运行的逻辑图

1. 列出逻辑状态表

A	B	C	G1	G2
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

2. 写出逻辑表达式

\[\begin{aligned} G_{1} & = \overline{A}BC + A\overline{B}C + AB\overline{C} + ABC = AB + BC + AC \\ G_{2} & = \overline{A}\overline{B}C + \overline{A}B\overline{C} + A\overline{B}\overline{C} + ABC \end{aligned} \]

3. 用与非门构成逻辑电路

\[G_{1} = AB + BC + AC = \overline{\overline{AB}\cdot\overline{BC}\cdot\overline{AC}} \]

\[G_{2} = \overline{A}\overline{B}C + \overline{A}B\overline{C} + A\overline{B}\overline{C} + ABC = \overline{\overline{\overline{A}\overline{B}C}\cdot\overline{\overline{A}B\overline{C}}\cdot\overline{A\overline{B}\overline{C}}\cdot\overline{ABC}} \]

4. 画出逻辑图