计数杂题。
calc
考虑先不管数字之间的顺序,最后给答案乘上一个 \(n!\)。
记 \(dp_{i,j}\) 表示前 \(i\) 个数在 \([1,j]\) 之间选,所产生的总贡献,显然有 \(dp_{i,j}=dp_{i,j-1}+j\times dp_{i-1,j-1}\),最后的答案是 \(dp_{n,k}\)。
发现 \(dp_n\) 是一个 \(2n\) 次多项式,拉插一下随便做。
最长上升子序列
好题。
记 \(f_i\) 表示前 \(i\) 个数组成的序列的 LIS 长度。
考虑将 \(1\sim n\) 依次插入序列,即时维护整个 \(f\) 数组,可以发现 \(f_i-f_{i-1}\le 1\),因此我们可直接维护 \(f\) 数组的差分。
考虑插入一个数会对 \(f\) 数组产生什么影响,首先是在这个位置的差分数组插入一个 1,再把后面的第一个 1 变成 0(具体可以自己画一画)。
也就是说,我们可以在 \(\sum\limits_{i=1}^ni2^i=O(n2^n)\) 的时间复杂度内求解,但是你发现这玩意要跑 10+s 啊。
发现这个题一共就这么几种输入,直接打表就可以了。
注意开数组的时候因为 \(f_1\) 一定等于 1,所以可以只开到 \(2^27\),然后再滚动一下空间就没有什么压力了。
Decreasing Subsequence
发现这个 \(a_i\le i\) 很不好做,考虑将所有的 \(a_i\) 减 1,然后让 \(i\) 向 \(a_i'\) 连边,可以发现最终的图是若干条互不相交的链,且每条链都是从最后的节点不断向前连边。
然后考虑一下长度为 \(k\) 的下降子序列在图上是个什么样子:
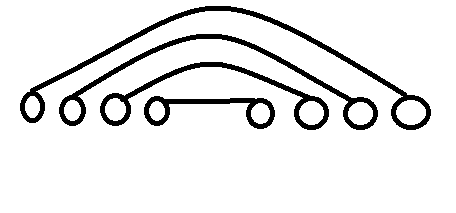
这是 \(k=4\) 的情况,发现就是要求有 \(k\) 条依次包含的边。
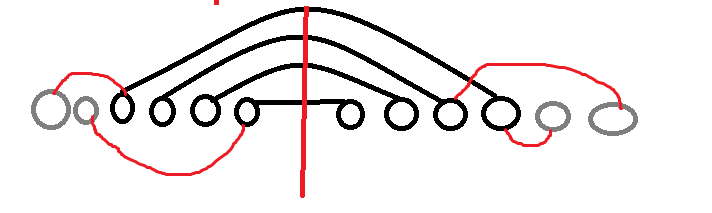
考虑 \(k\) 条边所在的 \(k\) 条链,假设一共有 \(i+j\) 个点,在中线的左侧 \(i\) 个,右侧 \(j\) 个。如果左右两边的情况都确定了,那剩下的中间 \(k\) 条边的连法是唯一确定的,即一共 \({i\brace k}{j\brace k}\) 种方案。其余的 \(n+1-i-j\) 个点可以随便连边,也就是一共 \(\sum\limits_{t}{n+1-i-j\brace t}=bell_{n+1-i-j}\) 种,因此答案就是 \(\sum_{i}\sum_{j}{n+1\choose i+j}{i\brace k}{j\brace k}bell_{n+1-i-j}\)。
随机立方体
简单题,随便做。
考虑二项式反演,钦定了 \(k\) 个位置是极大的数