并行前缀（Parallel Prefix）加法器

并行前缀（Parallel Prefix）加法器

并行前缀加法器的基本介绍

二进制加法器是目前数字计算单元中的重要模块，基础的加法器架构包括行波进位加法器（Ripple Carry Adder），超前进位加法器（Carry Look-Ahead Adder），进位选择加法器（Carry Select Adder）等。加法器的进位传播是其组合延迟的主要来源，在现代的高性能计算中，快速的加法器结构可以决定系统的运行，为了降低进位传播延迟，大部分现代加法器结构会采用并行前缀加法器（Parallel Prefix Adder）

并行前缀加法器根据拓扑的不同，可以分类为不同的类型，类如Kogge Stone Adder，Sklansky Adder，Brent Kung Adder，Han Carlson dder，Lander Fischer Adder等。不同的拓扑会具备不同的延迟、面积、功耗属性，需要在设计中酌情考虑。

并行前缀加法器的原理

并行前缀加法器通过三个基本阶段来实现加法操作，分别为：

1. \(P_i\)与\(G_i\)的预运算
2. 进位传播网络
3. 后运算

第一个阶段是\(P_i\)与\(G_i\)的预运算，用于根据输入\(A\)和\(B\)的对应相加的每对比特产生生成（generate）和传播（propagate）信号，根据公式：

\[p_i=a_i \oplus b_i \]

\[g_i=a_i \cdot b_i \]

第二个阶段的进位传播网络是不同拓扑的进位前缀加法器产生延迟、面积、功耗差异的来源，对加法器起到决定性因素，其包含了处理单元和缓冲单元，更少的处理单元意味着更小的延迟，而缓冲单元的输出则与输入相同。处理单元的输出为：

\[g_{i,k}=g_{i,j}+p_{i,j}\cdot g_{j-1,k} \]

\[p_{i,k}=p_{i,j}\cdot p_{j-1,k} \]

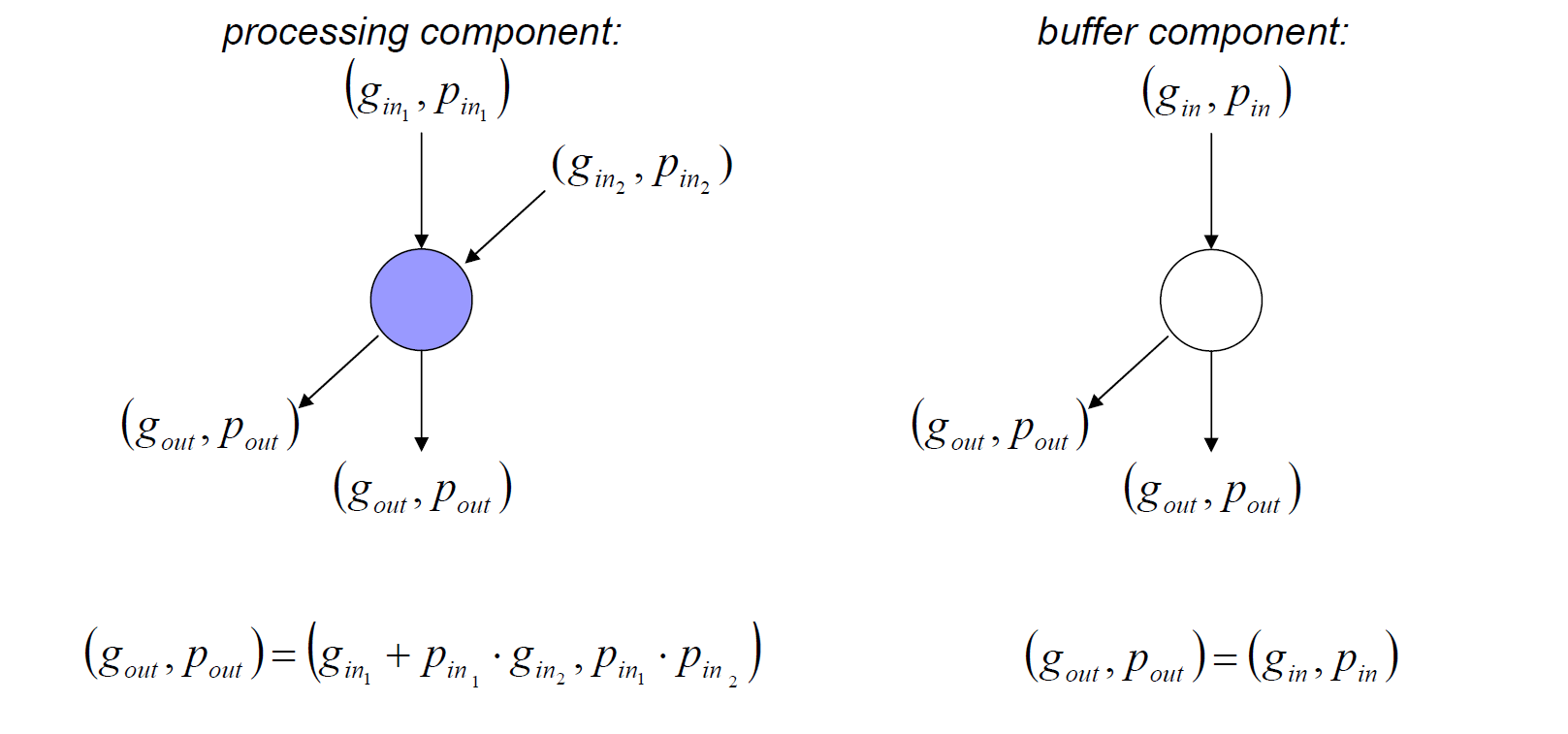
第三阶段的后处理单元完成最终的求和与进位运算：

\[s_i=p_i\cdot g_{i-1,1} \]

\[c_{out}=g_{n,1} \]

关于这里的标号的含义，可以参考下图：

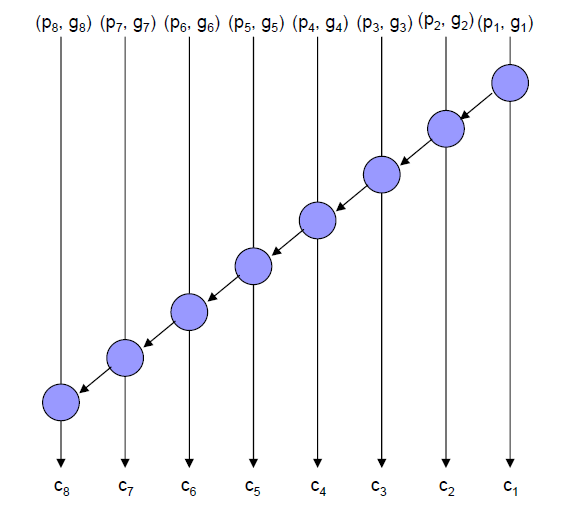
假定一个8bit的加法器结构（这个拓扑本质上是一个串级加法器），一共产生了8对初始的\(p_i\)和\(g_i\)，这里\(i=1,2,3,4\dots 8\)，除了进位链上的第一个处理单元之外，每个处理单元接收两对\((p,g)\)的输入，为了标记两对输入的来源，我们采用一对标号进行表示，第一个标号表示处理单元处于第几位的箭头上。第二个标号表示了这对\((p,g)\)能够"溯源"到第几位的箭头上，即我们直接观察该输入对所属的进位传播链的源头对应在第几位的箭头上。例如对于进位传播链上的最后一个处理单元，他的两对\((p,g)\)对的输入，分别应该对应\((p_8,g_8)\)，根据前面所述规则，可以看作是\((p_{8,8},g_{8,8})\)和\((p_{7,1},g_{7,1})\)，并根据处理单元的公式，产生\((p_{8,1},g_{8,1})\)，根据后处理单元的公式，这一位的\(s_8=p_8\cdot g_{7,1}\)，同时最终的进位为\(c_{out}=g_{8,1}\)。

从根本的数学原理上来说，实际上并行前缀加法器与超前进位加法器一致，基于相同的进位比特产生方程式。因为超前进位加法器属于教科书上基本都会讲解的加法器结构，这里不对其细节再做赘述。

并行前缀加法树的拓扑

在上一小节中我们提到了根据进位传播网络的不同，并行前缀加法器可以形成不同延迟、面积、功耗属性的拓扑。具体来说，这里以8bit加法器为例简单展示几种：

Kogge Stone Adder：

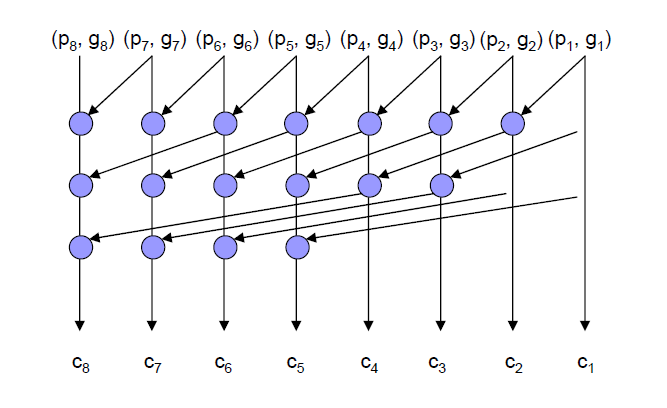
Sklansky Adder：

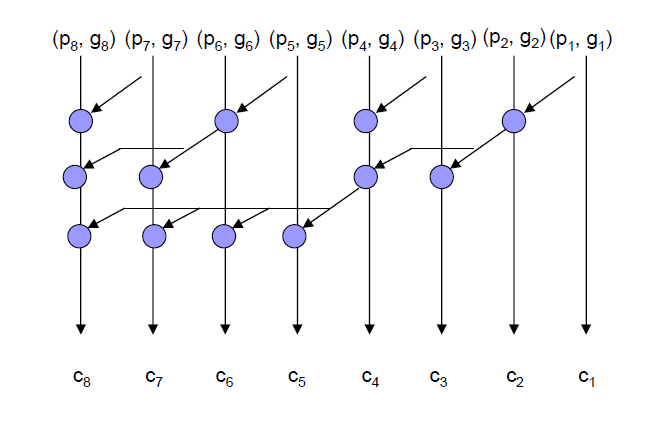
Brent Kung Adder：

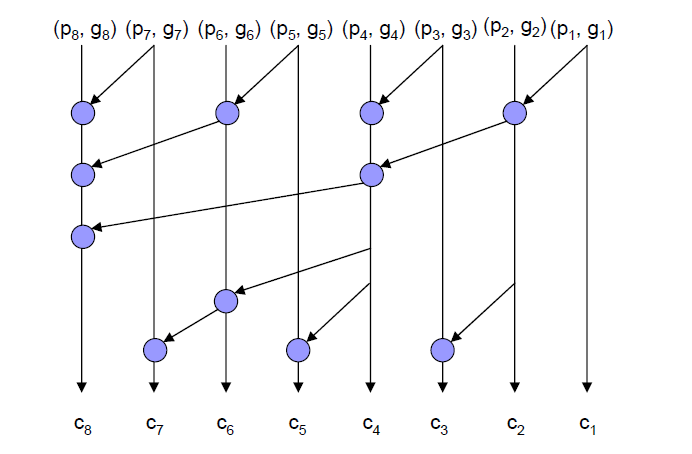
对于不同拓扑的比较可见下表，在TSMC 90nm工艺下，以64bit位宽加法器作为对象，不同拓扑的属性情况：

可以看出，在延迟上Kogge Stone拓扑具有最显著的优势，而Brent Kung拓扑虽然在延迟上表现最差，但具有最优的面积和功耗。面积和功耗可以理解为受到处理单元个数的影响，而延迟则受到最大延迟传播链上处理单元数量的影响，从上面展示的图中可以显著的看出各个拓扑的差异。

并行前缀加法器的发展方向

由于AI的快速发展，高性能计算的需求暴涨，如何设计出合理的拓扑满足延迟、面积、功耗的平衡是一个复杂的问题。

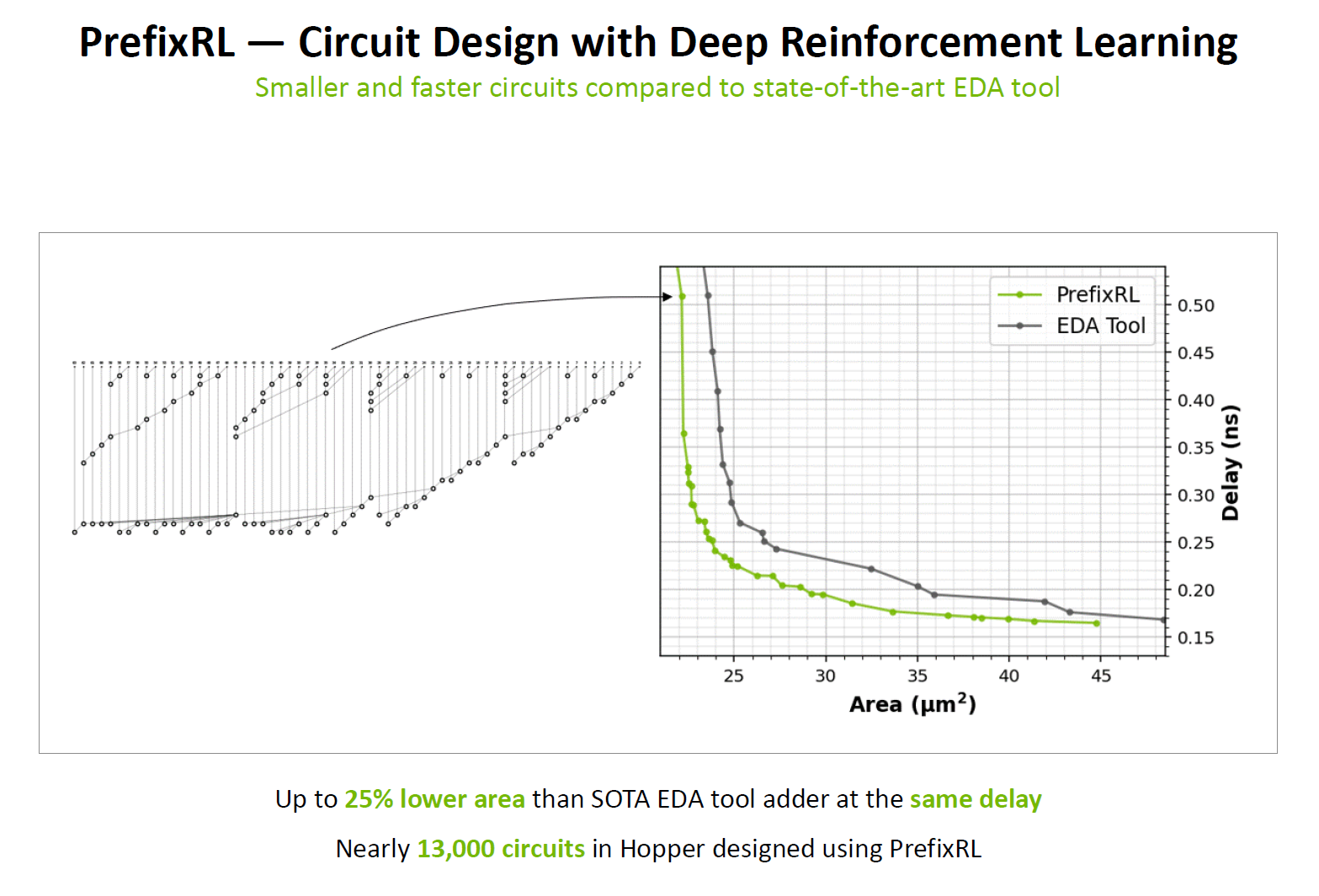
在ISSCC2024的Plenary上，英伟达介绍了他们通过结合了强化学习策略实现的PrefixRL工具在并行前缀的拓扑上取得了比现有SOTA EDA工具更好的优化效果，实现了综合面积、延迟更好的并行前缀加法器电路。PrefixRL工具被用于了Hopper GPU中接近13000个电路的设计。

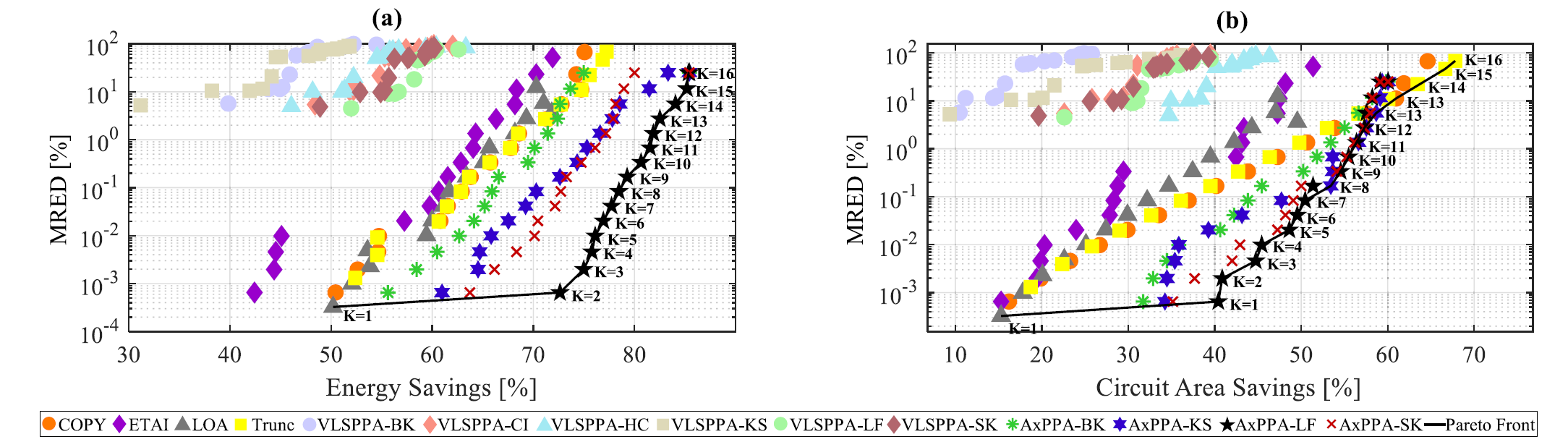
此外对于具备一定的容错性的计算负载，可以通过近似计算的优化手段来牺牲计算准确度换取更好的综合性能表现，Morgana Macedo Azevedo da Rosa等人提出了一种近似并行前缀加法器结构，在相同的MRED（平均相对错误距离）下，取得了相对于传统近似加法器结构，如LOA，Trunc，ETAI等更好的能耗和面积节省。

参考文献

1. "A Comparative Analysis of Parallel Prefix Adders", Megha Talsania et. al.
2. "Parallel Prefix Adders- A Comparative Study For Fastest Response", Er. Aradhana Raju et. al.
3. "Parallel prefix adders", KostasVitoroulis
4. "AxPPA: Approximate Parallel Prefix Adders", Morgana Macedo Azevedo da Rosa et. al.