摘樱桃II

news/2025/1/11 12:50:35/文章来源:https://www.cnblogs.com/Xhita/p/18665342

摘樱桃II

“作为一个合格的程序员，理应具有修bug修到凌晨4点的魄力”

戳我查看原题。

题目大意

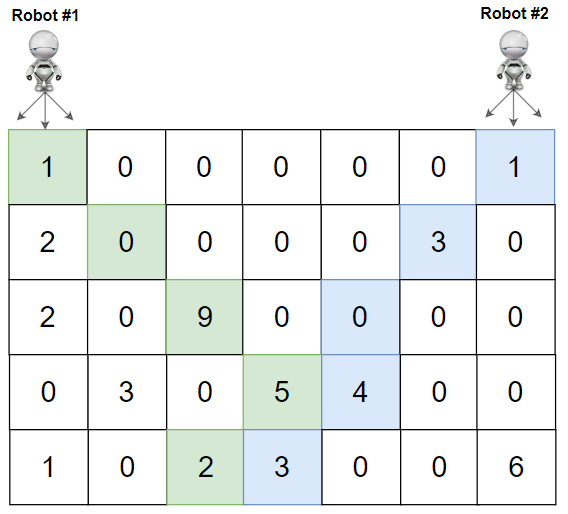
给定一个矩阵，矩阵中的每个数代表该点的樱桃个数。Robot1、Robot2分别从左上角与右上角出发，每次只能选择向正下方、左下方、右下方三个方向移动去采摘樱桃，到达矩阵的最后一行终止。若Robot1与Robot2到达同一个位置，则只有一个Robot可以获得到该点的樱桃。求Robot1与Robot2所能采摘到的最大樱桃数；

思路

这是一道简单的dfs,直接记忆化暴力搜索！（误

本人采用的是dp；由于R1与R2只能向3个方向前进，所以可以看作简单二维dp板子题的进阶版（板子题链接）：统计每一层R1与R2所有可能出现的状态，在每个状态的多种不同的可能值中去取最大值作为该状态的最优解，接着在最后一层中选择樱桃最多的状态输出就能完美解决该问题。

如何记录每一层R1与R2的状态

开一个三维状态数组f[t][i][j]，t表示层数，i表示robot1的状态，j表示robot2的状态；

如何推得状态方程

在理想状态下对于某一状态f[t][i][j]的robot1与robot2都有三种不同的来源，以robot1为例：位于第t层(行)第i列的robot1可以由位于第t-1层(行)第i列或第i-1列或第i+1列得到，于是乎我们便可得到f[t][i][j]的上一状态，写作状态方程为：

f[t][i][j]=max(

{f[ t - 1 ][ i ][ j ],f[ t - 1 ][ i - 1 ][ j ],f[ t - 1][ i + 1 ][ j ],

f[ t - 1 ][ i ][ j - 1 ],f[ t - 1 ][ i - 1 ][ j - 1 ],f[ t - 1 ][ i + 1 ][ j - 1 ],

f[ t - 1 ][ i ][ j + 1 ],f[ t - 1 ][ i - 1 ][ j + 1 ],f[ t - 1 ][ i + 1 ][ j + 1 ]})+grid[ t ][ i ] + grid[ t ][ j ];(grid表示该点的樱桃数)

范围问题

对于robot1，若它每次都向右下方前行则i=t，t即为i的上值；同时，我们不难推出robot2与robot1相遇是一个必然会被舍弃的情况，所以i同时也要小于j,既0<i<=min( t , j - 1 );同理我们也可以推出j的取值范围：max( i + 1 , n - t +1 )<=j<=n;

代码

点击查看代码

class Solution {
public:int cherryPickup(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size(),rema=0;//rema用来记录达到最后一层时的最大值vector<vector<vector<int>>> f(m+1,vector<vector<int>>(n+2, vector<int>(n+2,0)));//建立状态数组，f[t][i][j]中t表示层数，i表示robot1的状态，j表示robot2的状态；
//有关三维vector的初始化有兴趣的可以去了解一下（申桑也是写这个题时才会的……）f[1][1][n]=grid[0][0]+grid[0][n-1];//起始状态（第一层）的初始化int di[]={1,1,1,0,0,0,-1,-1,-1},dj[]={0,-1,1,0,-1,1,0,-1,1};//定义向量数组，图论常用for(int t=2;t<=m;t++){//从第二层开始for(int i=1;i<min(t+1,n);i++){//注意范围！！！是谁范围写错改了一个多小时我不说（for(int j=n;j>max(i,n-t);j--){for(int d=0;d<9;d++){//向量的使用int x=i+di[d],y=j+dj[d];//用xy存储上一状态，也方便检测范围是否合法if(x>0&&x<min(t+1,y)&&y>max(x,n-t)&&y<=n){f[t][i][j]=max(f[t][i][j],f[t-1][x][y]);//先找出最大的上一状态}}f[t][i][j]+=(grid[t-1][i-1]+grid[t-1][j-1]);//加上该状态r1r2的值if(t==m)rema=max(rema,f[t][i][j]);//到达最后一层时开始筛选最大的末状态}}}return rema;//返回末状态}
};