题目
n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上,并且使皇后彼此之间不能相互攻击(每一行,每一列,每个对角线上只能有一个皇后存在)。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
示例 1:
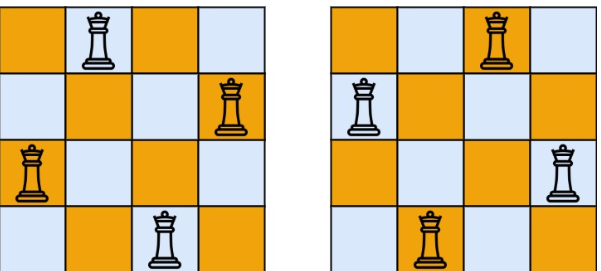
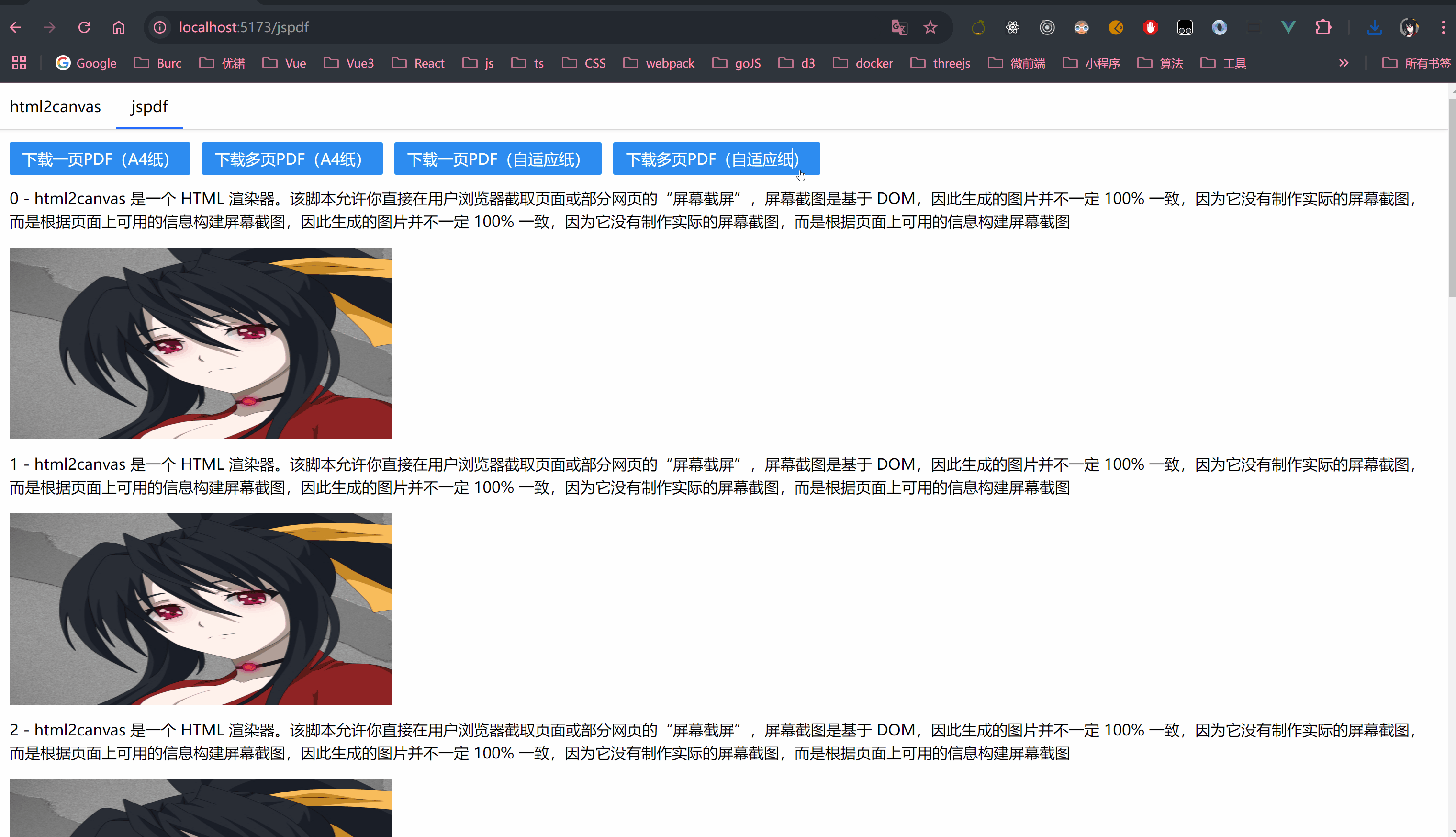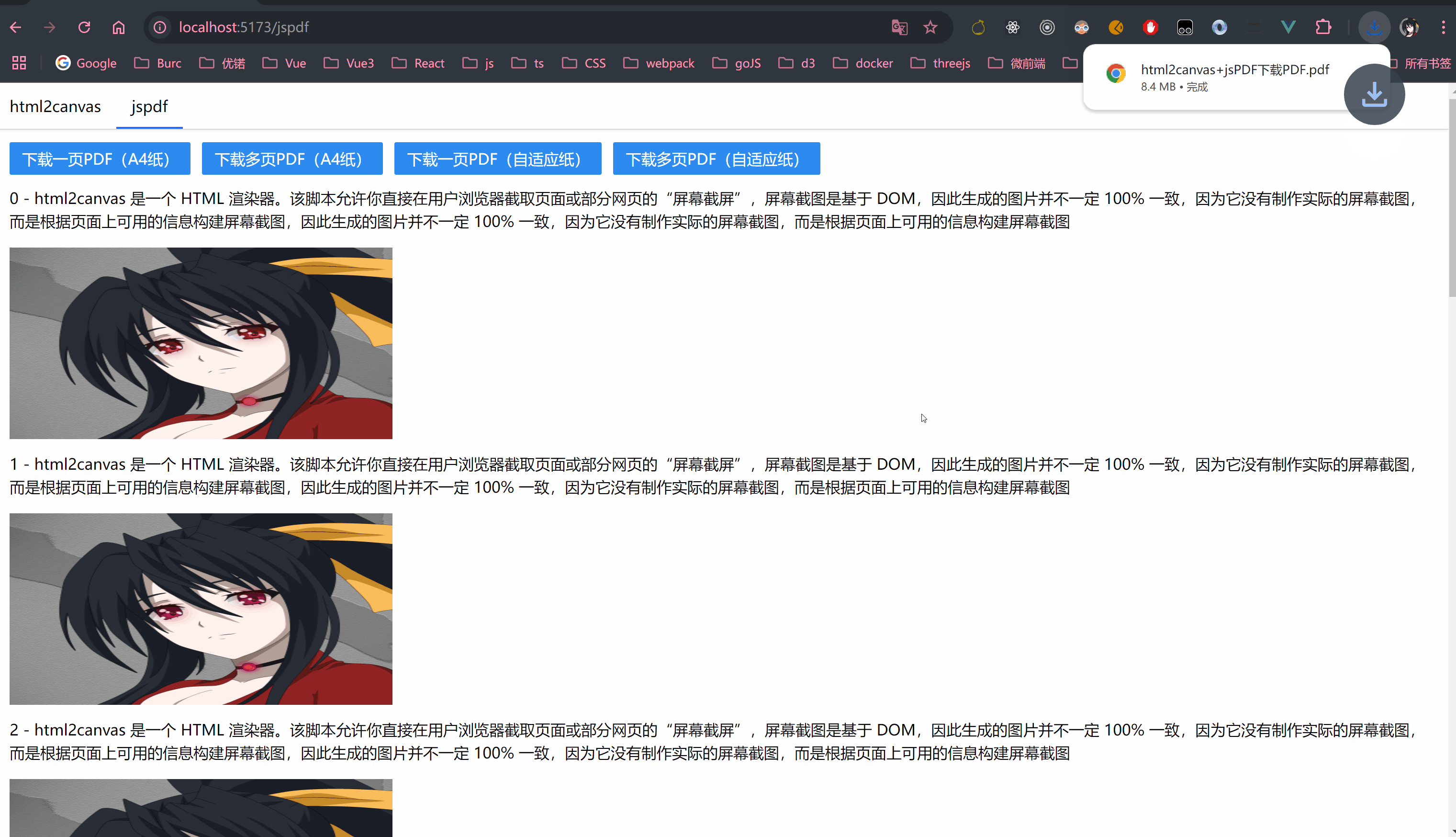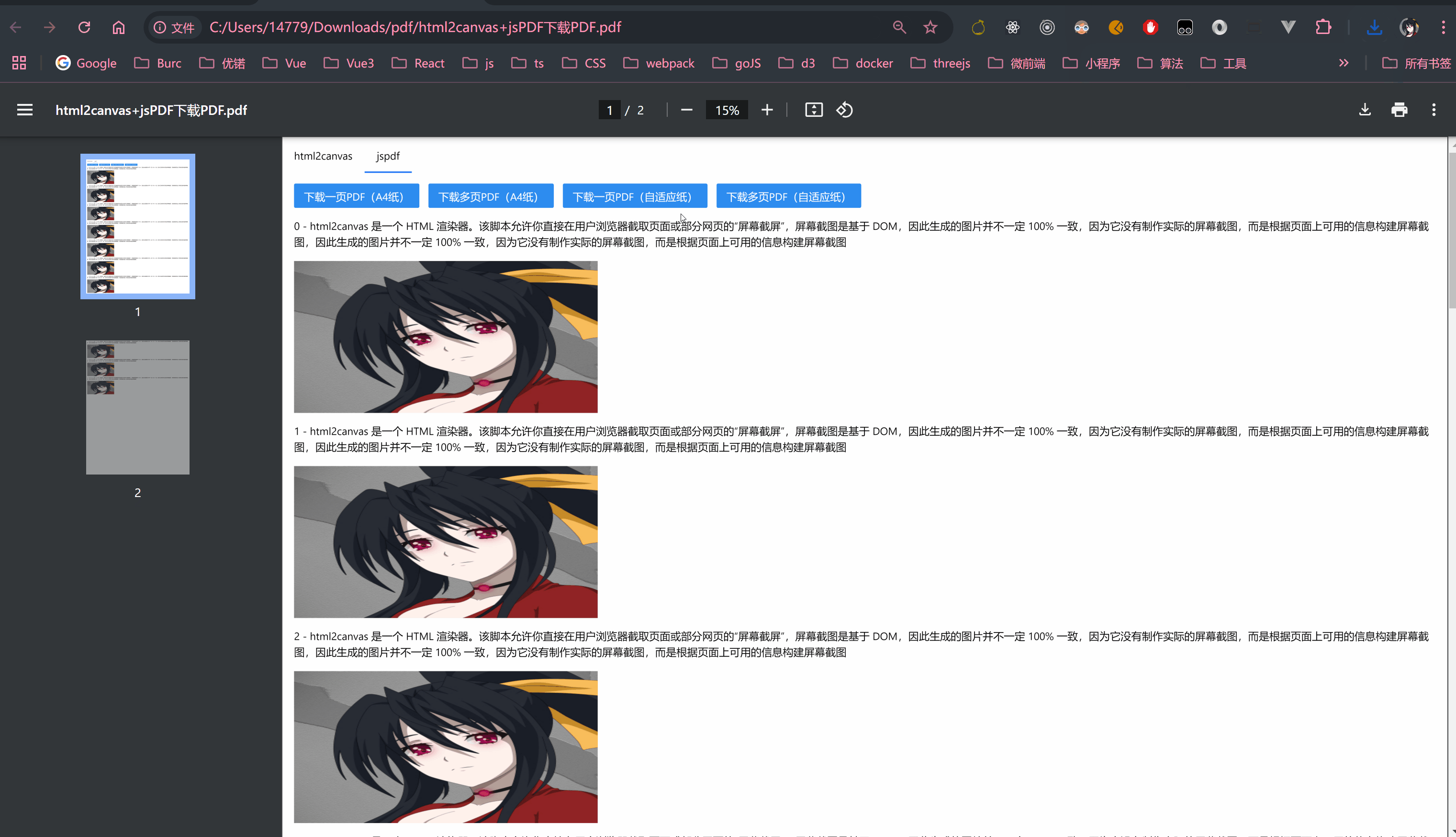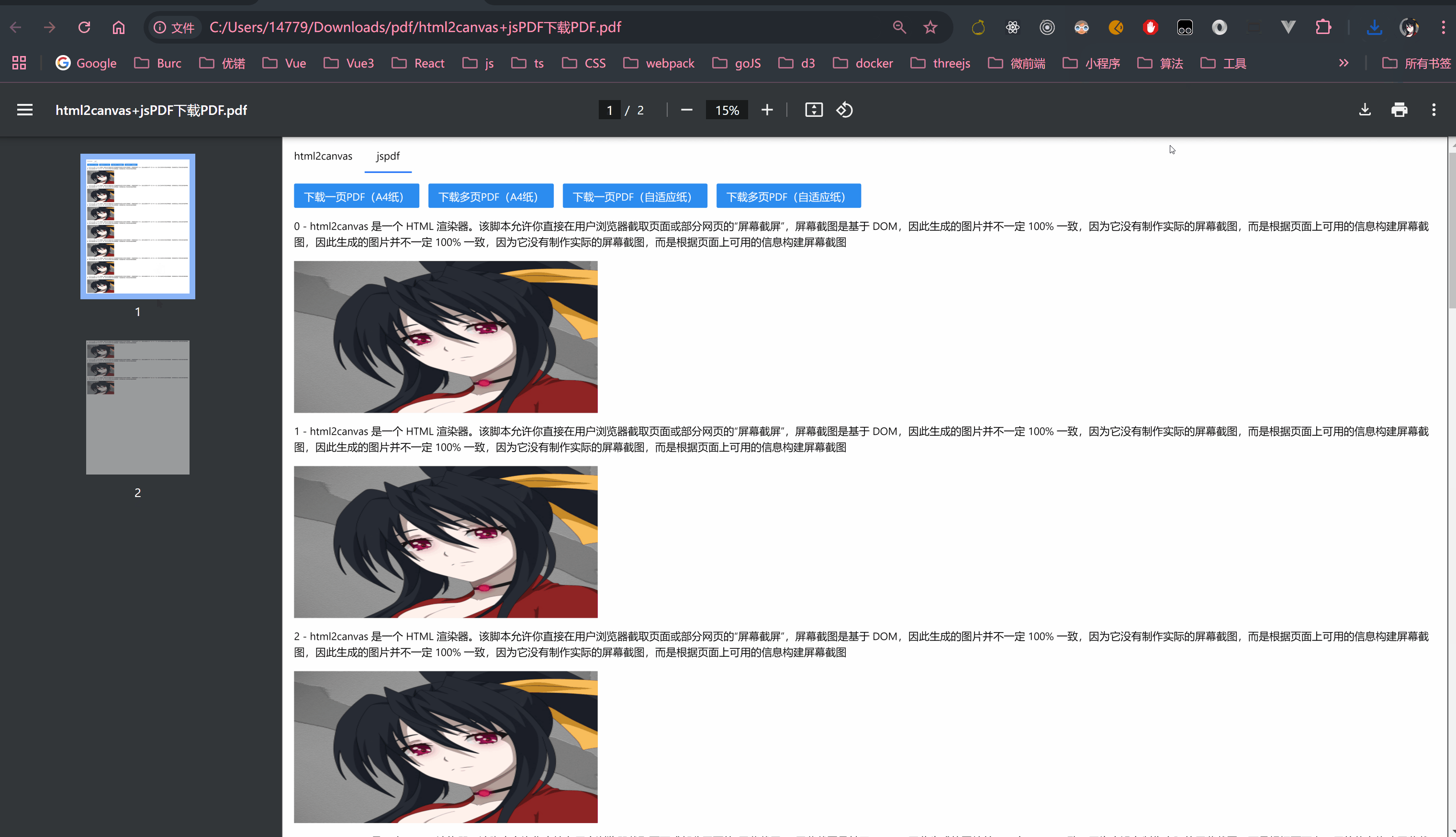
输入:n = 4
输出:2
解释:如上图所示,4 皇后问题存在两个不同的解法。
思路
采用暴力搜索,回溯剪枝标记处每一个已经存放的皇后的行和列以及对角线,表示以后这些位置以后不能再放皇后了,这里可以用数组标记,我这里采用的是位运算方法。
整形int类型二进制通常有32位,可以利用这个位数的状态(二进制中只有0和1)表示是否可以放皇后,比如1表示已经放过皇后了,那么只有0可以再放皇后。比如n=5,那么最初的状态就是00000,最后结束条件就是11111,表示所有位置都放了皇后
代码
class Solution {
public:int dfs(int limit,int col,int left,int right){if(col==limit){return 1;}//这是搜索到最后一列的条件,表示找到一种方法可以放皇后,并开始返回int ban=col|left|right;//放皇后的位置有3个限制(因为行在不断向下搜索,所以只用考虑每一列,不用考虑行),
//考虑列,左上到右下对角线(left),右上到左下对角线(right),比如列1000,left对角线0100,right对角线0010,那么|就把所有的1聚集到一起变成1110,表示只有0这个位置可以放皇后int candiate=limit&(~ban);//先把ban取反(1变成0,0变成1),那么就是只有1的位置可以放皇后,n=5时,limit=11111,&保留了5个位内所有的1int place=0;int ans=0;while(candiate!=0){//如果candiate==0表示所有位置都占满place=candiate&(-candiate);//获得最近的一个1,比如10010,操作之后变成00010,只剩下最近的一个1,candiate^=place;//异或操作,把放皇后的这一列标记一下ans+=dfs(limit,(col|place),(left|place)>>1,(right|place)<<1);//这里|操作把1聚集,每一列直接标记,但是left对角线比如上一行100(第一个1不能放皇后),
//那么下一列就应该是010表示这个对角线位置不能放皇后,right对角线也是如此}return ans;}int totalNQueens(int n) {int limit=(1<<n)-1;//比如n=5,那么limit=11111,因为int有32位但是我们只需要5位,那么就用这个值限制出来5位,其他位上的值通过&运算都可变为无效值return dfs(limit,0,0,0);}
};