A - Humidifier 1
题意:一个漏水的桶,在零时刻有零升水,进行\(n\)次加水,在\(t_i\)时刻加\(v_i\)升水,每一时刻会漏一生水,问第n次加水后有多少升水。
直接模拟即可,每次加水先减去漏掉的水,注意至少有0升,然后加上新加的水。
点击查看代码
void solve() {int n;std::cin >> n;int last = 0, sum = 0;for (int i = 0; i < n; ++ i) {int a, b;std::cin >> a >> b;sum = std::max(0, sum - (a - last));sum += b;last = a;}std::cout << sum << "\n";
}
B - Humidifier 2
题意:一个矩阵有墙有地板,你可以在两个地板上各放一个加湿器,加湿器会加湿距离他曼哈顿距离小于等于d的地板,你最多可以加湿多少地板。
直接枚举放在哪两个地板就行。
点击查看代码
void solve() {int n, m, d;std::cin >> n >> m >> d;std::vector<std::string> s(n);for (int i = 0; i < n; ++ i) {std::cin >> s[i];} auto get = [&](int x, int y, int i, int j) -> bool {return std::abs(x - i) + std::abs(y - j) <= d;};int ans = 0;for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (s[i][j] == '#') {continue;}for (int x = 0; x < n; ++ x) {for (int y = 0; y < m; ++ y) {if (s[x][y] == '#') {continue;}int cnt = 0;for (int l = 0; l < n; ++ l) {for (int r = 0; r < m; ++ r) {if (s[l][r] == '.' && (get(i, j, l, r) || get(x, y, l, r))) {++ cnt;}}}ans = std::max(ans, cnt);}}}}std::cout << ans << "\n";
}
C - Humidifier 3
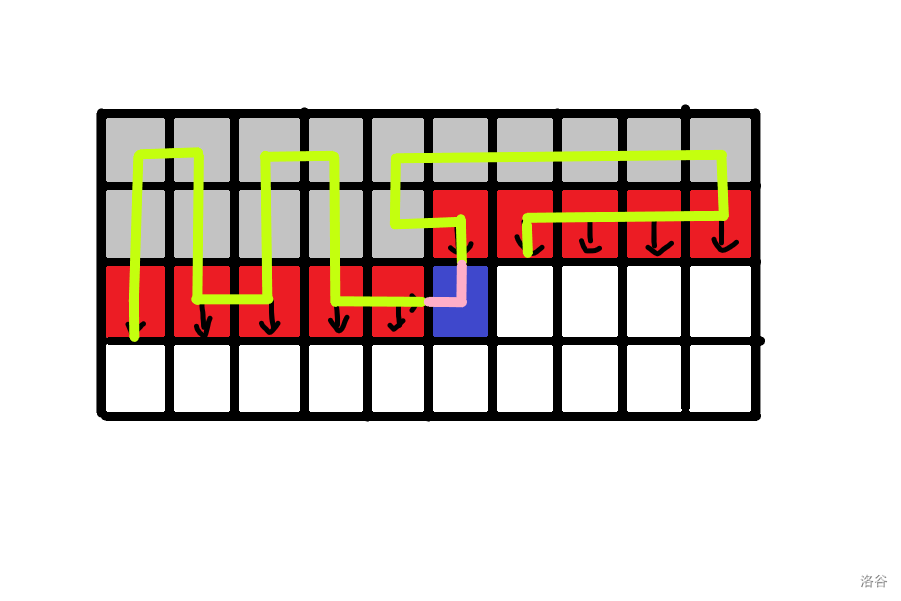
题意:一个矩阵有墙有地板有加湿器,加湿器会加湿最短距离距离他小于等于d的地板,但这个路径中不能穿墙,问可以加湿多少地板。
bfs。
先把所有加湿器入队,用个dist存每个格子最多可以走的步数,统计所有可以走到的地板。
点击查看代码
void solve() {int n, m, d;std::cin >> n >> m >> d;std::vector<std::string> s(n);for (int i = 0; i < n; ++ i) {std::cin >> s[i];}std::vector dist(n, std::vector<int>(m));std::queue<std::pair<int, int> > q;for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (s[i][j] == 'H') {dist[i][j] = d + 1;q.push({i, j});}}}const int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};while (q.size()) {auto [x, y] = q.front(); q.pop();for (int i = 0; i < 4; ++ i) {int nx = x + dx[i], ny = y + dy[i];if (nx < 0 || nx >= n || ny < 0 || ny >= m || s[nx][ny] == '#' || dist[nx][ny] > dist[x][y] - 1) {continue;}dist[nx][ny] = dist[x][y] - 1;q.push({nx, ny});}}int ans = 0;for (int i = 0; i < n; ++ i) {for (int j = 0; j < m; ++ j) {if (s[i][j] != '#' && dist[i][j] > 0) {++ ans;}}}std::cout << ans << "\n";
}
D - 9 Divisors
题意:问有多少恰好有九个因子的小于等于n的数。
刚开始以为是爆搜。。。
我们知道一个数有多少因子跟它的质因子有关,于是我们手玩一会后发现只有两种形式的数满足,一个数等于 \(p_1^2\)乘\(p_2^2\)的数,一个是等于\(p_i^8\)的数。
于是我们筛出所有质数后,二分每个质数能匹配到的最大质数,再看有哪些一个就可以的。
点击查看代码
void solve() {i64 n;std::cin >> n;const int N = 2e6 + 5;std::vector<i64> primes;std::vector<int> st(N);for (int i = 2; i < N; ++ i) {if (!st[i]) {primes.push_back(i);}for (auto & p : primes) {if (p > N / i) {break;}st[p * i] = 1;if (i % p == 0) {break;}}}i64 ans = 0;for (int i = 0; i + 1 < primes.size(); ++ i) {int l = i + 1, r = (int)primes.size() - 1;while (l < r) {int mid = l + r + 1 >> 1;i64 x = primes[i], y = primes[mid];if ((__int128)x * x * y * y <= n) {l = mid;} else {r = mid - 1;}}i64 x = primes[i], y = primes[l];if ((__int128)x * x * y * y <= n) {ans += l - i;} else {break;}if ((__int128)x * x * x * x * x * x * x * x <= n) {++ ans;}}std::cout << ans << "\n";
}题意:给你一个图和两个序列A和B,A中的数和B都不相同。 设\(f(u, v)\)是u到v中所有路径的最大边权中最小的。你可以打乱B的顺序,求最小的\(\sum_{i=1}^{k} f(A_i, B_i)\)。
先阅读最小生成树和瓶颈生成树以及最小瓶颈路的概念:https://oi-wiki.org/graph/mst/#瓶颈生成树
那么我们知道\(f(u, v)\)对应的边肯定在最小生成树里,我们可以按照\(Kruskal\)算法的顺序从小到大加边,那么我们发现,当加入一条边\((u, v)\)时,在此之前还没找到瓶颈路径的两个点,如果正好在合并的这两个联通块里,那么这条边就是他们最小瓶颈边,于是贪心的尽可能匹配就行,存一下每个集合在\(A\)里有多少点和在\(B\)里有多少点。
点击查看代码
void solve() {int n, m, k;std::cin >> n >> m >> k;std::vector<std::array<int, 3> > edges(m);for (int i = 0; i < m; ++ i) {int u, v, w;std::cin >> u >> v >> w;-- u, -- v;edges[i] = {w, u, v};}std::sort(edges.begin(), edges.end());std::vector<int> fa(n), cnta(n), cntb(n);std::iota(fa.begin(), fa.end(), 0);for (int i = 0; i < k; ++ i) {int x;std::cin >> x;-- x;++ cnta[x];}for (int i = 0; i < k; ++ i) {int x;std::cin >> x;-- x;++ cntb[x];}std::function<int(int)> find = [&](int x) -> int {return x == fa[x] ? x : fa[x] = find(fa[x]);};i64 ans = 0;for (auto & [w, u, v] : edges) {u = find(u), v = find(v);if (u == v) {continue;}fa[v] = u;cnta[u] += cnta[v];cntb[u] += cntb[v];int min = std::min(cnta[u], cntb[u]);ans += (i64)min * w;cnta[u] -= min;cntb[u] -= min;}std::cout << ans << "\n";
}