LibreOJ-3614 Luogu-P9040
很好的题。
先不考虑区间,先想 \(l=1,r=n\) 的情况。
考虑 dp,\(f_i\) 表示考虑 \([l,r]\) 的答案。
则容易得到:
其中 \(s\) 为 \(a\) 的前缀和。
这个转移本身是 \(\Theta(n)\) 的。
遇见这种区间查询 DP 的通常都是动态 DP,但是由于下标跨了 \(k\),矩阵的大小为 \(\Theta(k)\),所以进行如此操作的时间复杂度为 \(\Theta(k^3\log n)\),表现很差。
本题难点在此。
我们看到这个 DP 式子非常工整,灵光一现,唉我给她塞图上。
我们从 \(u\) 向 \(v\) 连长度为 \(w\) 的边表示 \(f_v\) 的转移方程式里有一项为 \(f_u + w\)。
突破口出现了!
原题所求的 \([l,r]\) 的答案就是 \(l-1\) 到 \(r\) 的最长路!(注意此处由于 \(l\) 也要参与运算,所以起点为 \(l-1\))
但是新的问题到来了,怎么给这样一个图求两点最短路呢?
显然不能 Johnson,这样比暴力还慢。
显然是要利用这个图的结构。
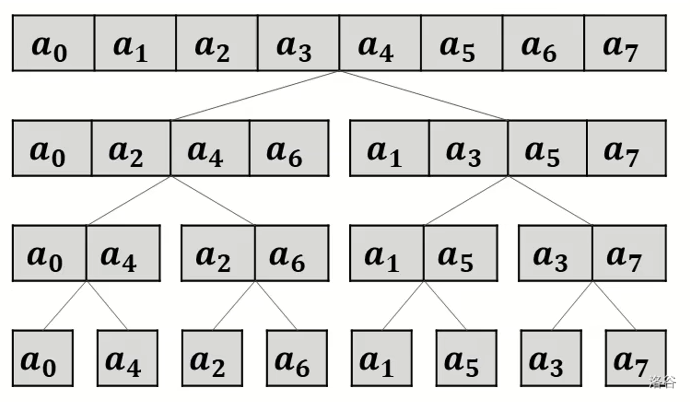
我们经过一顿梳理发现她长这样。

规规整整的跟个矩形一样。
知道网格求最短路的同学瞬间就懂了。
接下来是个很经典的 trick。
对于一类网格图,我们若要求若干点对间的最短或长路则采用以下算法:
我们考虑把询问离线下来分治。
每次分治面向原网格中的一个子网格。
为了方便我们设她是 \(r\times c\) 的。
\(1^\circ\) 若 \(r>c\),我们按照中间行把她切成两半,对于中间行上每个点 \(p\) 算出其对子矩阵里所有点的最短或长路。(若是 DAG 则可直接 DP),然后枚举所有被这个中间行分开的点对 \(u,v\),将 \(u\) 到 \(v\) 的最短或长路经过 \(p\) 松弛。(因为 \(u\) 到 \(v\) 的最短或长路一定经过 \(p\))
\(2^\circ\) 不然则按照中间列切,同样枚举中间列上的点来计算。
每次把切完的两个小网格分治下去,要把两端点都在。
每次分治 \(O(n\sqrt n)\)。
由主定理,总复杂度 \(O(n\sqrt n)\)。
回到这道题。
我们发现还有一些从最顶上指到底下的边,他们可以通过这条边而不需通过中间行。
对于这种情况我们可以额外枚举第一行的每个点,因为经过斜边一定要经过第一行的点。
但是有可能在同一侧的节点的最长路穿下去再慢慢爬上来的情况。
这种情况我们也要给在同一侧的点对统计答案,但是由于只有一次不影响复杂度。
#pragma GCC optimize("Ofast", 3, 2, 1)
#include <bits/stdc++.h>
using namespace std;#define int long long
#define endl '\n'
#define debug(x) cerr << #x << " = " << x << endl
#define rep(i, a, b) for (int i = (a); i <= (b); i++)
#define per(i, a, b) for (int i = (a); i >= (b); i--)
#define gn(u, v) for (int v : G.G[u])
#define pb emplace_back
#define mp make_pair
#define fi first
#define se second
#define sz(x) (int)(x).size()
#define pii pair<int, int>
#define vi vector<int>
#define vpii vector<pii>
#define vvi vector<vi>
#define no cout << "NO" << endl
#define yes cout << "YES" << endl
#define all(x) x.begin(), x.end()
#define rall(x) x.rbegin(), x.rend()
#define tomin(x, y) ((x) = min((x), (y)))
#define tomax(x, y) ((x) = max((x), (y)))
#define ck(mask, i) (((mask) >> (i)) & 1)
#define pq priority_queue
#define FLG (cerr << "Alive!" << endl);constexpr int MAXN = 6e5 + 5;
constexpr int INF = 0x3f3f3f3f3f3f3f3f;
int n, k, q;
int a[MAXN];
vector<vpii> G;
vector<vpii> H;struct Query {int u, v, ans;
};
vector<Query> query;vi num[MAXN];
int x[MAXN], y[MAXN];
int dis[2][MAXN];void get(int start, const vector<vpii> &G, const vector<vpii> &H, int lx, int rx, int ly, int ry, bool typ) {// rep(i, lx, rx) {// rep(j, ly, ry) {// dis[typ][num[i][j]] = -INF;// }// }vi vis;if (typ) {per(j, ry, ly) {per(i, rx, lx) {if (num[i][j] > start && !typ)vis.pb(num[i][j]);if (num[i][j] < start && typ)vis.pb(num[i][j]);}}} else {rep(j, ly, ry) {rep(i, lx, rx) {if (num[i][j] > start && !typ)vis.pb(num[i][j]);if (num[i][j] < start && typ)vis.pb(num[i][j]);}}}dis[typ][start] = 0;for (int u : vis) {if (u == start)continue;dis[typ][u] = -INF;for (auto [v, w] : H[u]) {if (x[v] < lx || x[v] > rx || y[v] < ly || y[v] > ry)continue;// if (u == 200)// cerr << v << " " << w << " " << typ << endl;if (!typ && v >= start)tomax(dis[typ][u], dis[typ][v] + w);if (typ && v <= start)tomax(dis[typ][u], dis[typ][v] + w);}// cerr << "dis from " << start << " to " << u << " with type " << typ << " is " << dis[typ][u] << endl;// if (u == 200) {// cerr << dis[typ][u] << endl;// }}
}void solve(int lx, int rx, int ly, int ry, vector<Query> &q) {if (lx > rx || ly > ry || q.empty())return;rep(i, lx, rx) {rep(j, ly, ry) {dis[false][num[i][j]] = dis[true][num[i][j]] = 0;}}if (rx - lx <= ry - ly) {int mid = ly + ry >> 1;vector<Query> l, r, now;for (auto [u, v, ans] : q) {if (y[u] < mid && y[v] < mid) {l.pb(Query{u, v, ans});} else if (y[u] > mid && y[v] > mid) {r.pb(Query{u, v, ans});} else {now.pb(Query{u, v, ans});}}rep(tmp, lx, rx) {int cur = num[tmp][mid];get(cur, G, H, lx, rx, ly, ry, false);get(cur, H, G, lx, rx, ly, ry, true);dis[0][cur] = 0;dis[1][cur] = 0;for (auto& [u, v, ans] : now) {// if (u == 170 && v == 200) {// cerr << cur << "." << lx << " " << rx << " " << ly << " " << ry << endl;// cerr << dis[0][u] << " " << dis[1][v] << " " << dis[1][u] << " " << dis[0][v] << endl;// }tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));// cerr << dis[0][u] << " " << dis[1][u] << " " << dis[0][v] << " " << dis[1][v] << endl;}// for (auto& [u, v, ans] : l) {// // if (u == 170 && v == 200) {// // cerr << lx << " " << rx << " " << ly << " " << ry << endl;// // cerr << dis[0][u] + dis[1][v] << " " << dis[1][u] + dis[0][v] << endl;// // }// tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));// // cerr << dis[0][u] << " " << dis[1][u] << " " << dis[0][v] << " " << dis[1][v] << endl;// }// for (auto& [u, v, ans] : r) {// // if (u == 170 && v == 200) {// // cerr << lx << " " << rx << " " << ly << " " << ry << endl;// // cerr << dis[0][u] + dis[1][v] << " " << dis[1][u] + dis[0][v] << endl;// // }// tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));// // cerr << dis[0][u] << " " << dis[1][u] << " " << dis[0][v] << " " << dis[1][v] << endl;// }}solve(lx, rx, ly, mid - 1, l);solve(lx, rx, mid + 1, ry, r);int i = 0, j = 0, cnt = 0;for (auto& [u, v, ans] : q) {if (y[u] < mid && y[v] < mid) {ans = l[i++].ans;} else if (y[u] > mid && y[v] > mid) {ans = r[j++].ans;} else {ans = now[cnt++].ans;}}} else {int mid = lx + rx >> 1;vector<Query> l, r, now;for (auto [u, v, ans] : q) {if (x[u] < mid && x[v] < mid) {l.pb(Query{u, v, ans});} else if (x[u] > mid && x[v] > mid) {r.pb(Query{u, v, ans});} else {now.pb(Query{u, v, ans});}}rep(tmp, ly, ry) {int cur = num[mid][tmp];get(cur, G, H, lx, rx, ly, ry, false);get(cur, H, G, lx, rx, ly, ry, true);dis[0][cur] = 0;dis[1][cur] = 0;for (auto& [u, v, ans] : now) {// if (u == 170 && v == 200) {// cerr << cur << " " << lx << " " << rx << " " << ly << " " << ry << endl;// cerr << dis[0][u] << " " << dis[1][v] << " " << dis[1][u] << " " << dis[0][v] << endl;// }tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));}// for (auto& [u, v, ans] : l) {// tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));// }// for (auto& [u, v, ans] : r) {// tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));// }}if (lx == 1 && rx == k) {rep(tmp, ly, ry) {int cur = num[lx][tmp];get(cur, G, H, lx, rx, ly, ry, false);get(cur, H, G, lx, rx, ly, ry, true);dis[0][cur] = 0;dis[1][cur] = 0;for (auto& [u, v, ans] : now) {// if (u == 170 && v == 200) {// cerr << cur << " " << lx << " " << rx << " " << ly << " " << ry << endl;// cerr << dis[0][u] << " " << dis[1][v] << " " << dis[1][u] << " " << dis[0][v] << endl;// }tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));}for (auto& [u, v, ans] : l) {tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));}for (auto& [u, v, ans] : r) {tomax(ans, max(dis[0][u] + dis[1][v], dis[1][u] + dis[0][v]));}}}solve(lx, mid - 1, ly, ry, l);solve(mid + 1, rx, ly, ry, r);int i = 0, j = 0, cnt = 0;for (auto& [u, v, ans] : q) {if (x[u] < mid && x[v] < mid) {tomax(ans, l[i++].ans);} else if (x[u] > mid && x[v] > mid) {tomax(ans, r[j++].ans);} else {tomax(ans, now[cnt++].ans);}}}
}signed main() {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n >> k >> q;int tmp = (n / k + 1) * k - 1;rep(i, 1, n)cin >> a[i];rep(i, 1, tmp)a[i] += a[i - 1];G.resize(tmp + 1);H.resize(tmp + 1);rep(i, 1, tmp) {G[i - 1].pb(mp(i, 0));H[i].pb(mp(i - 1, 0));if (i >= k)G[i - k].pb(mp(i, a[i] - a[i - k])),H[i].pb(mp(i - k, a[i] - a[i - k]));}query.resize(q);rep(i, 0, q - 1) {cin >> query[i].u >> query[i].v;query[i].u--;query[i].ans = 0;}rep(i, 1, k) {num[i].resize(n / k + 2);}rep(i, 0, (n / k + 1) * k - 1) {num[i % k + 1][i / k + 1] = i;x[i] = i % k + 1;y[i] = i / k + 1;}// rep (i, 0, n) {// for (auto [v, w] : G[i]) {// cerr << i << " " << v << " " << w << endl;// }// }solve(1, k, 1, n / k + 1, query);// cerr << x[170] << " " << y[170] << " " << x[200] << " " << y[200] << endl;rep(i, 0, q - 1)cout << query[i].ans << endl;return 0;
}