Living-Dream 系列笔记第93期

news/2025/1/18 16:53:18/文章来源:https://www.cnblogs.com/XOF-0-0/p/18678545

本文讲解 EK & Dinic 算法。

最大流

最大流的模型：

特别注意：这个流量上限不是单次流量不超过它，而是多次的总和不超过它。

EK

显然这个问题是可以使用 dfs 解决的，但是效率低下。

考虑如下的图。

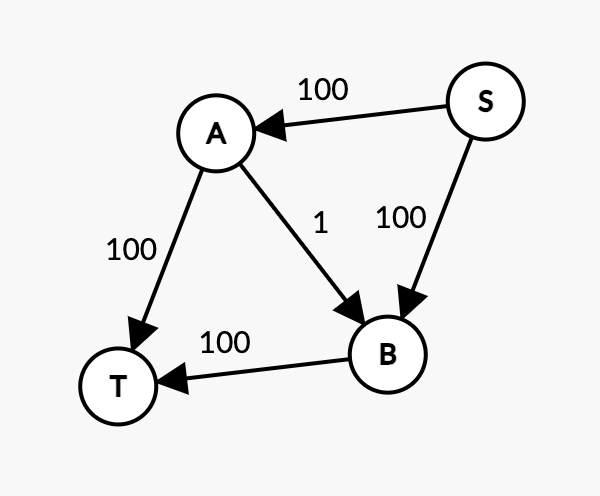
我们发现 dfs 有可能走了 \(S \to A \to B \to T\) 这样一条路线，这会导致 \(B \to T\) 流量上限减小 \(1\)，从而跑不出最优解，于是我们又需要新一轮的 dfs 来寻找最优解。这便是 dfs 效率低下的原因，即每次犯错都需要花费一轮或几轮的重新 dfs 来寻找最优解。

这启发我们思考，如何在一轮 dfs 中纠错？考虑建立反边，流量上限初始为 \(0\)。正边每次损耗多少流量，反边就加上多少流量。以上图为例，这样，如果 dfs 走了 \(S \to A \to B \to T\)，它就可以通过走 \(S \to B \to A \to T\) 来纠正它的错误，相当于 \(S \to A \to T\) 与 \(S \to B \to T\) 都跑了一遍 \(1\) 的流量。重复 \(100\) 次，即可在一轮 dfs 中求出最优解。这被称之为 FF 算法。

但是，很容易发现 FF 算法的时间复杂度取决于中间那条边的流量大小，当流量上限较大时，此算法的时间复杂度仍然很高。

有了纠错机制还不够，那么我们如何让 dfs 少犯错？考虑一种简单的贪心，我们可以总是走更短的路线，这样受的约束更少，更容易找到最优解。事实上，这个优化虽然看上去很 navie，但是它跑得飞快。找最短路用 bfs 即可解决。

综上便是 EK 算法的全部内容。

Dinic

考虑上述问题的一个特殊情况，如图。

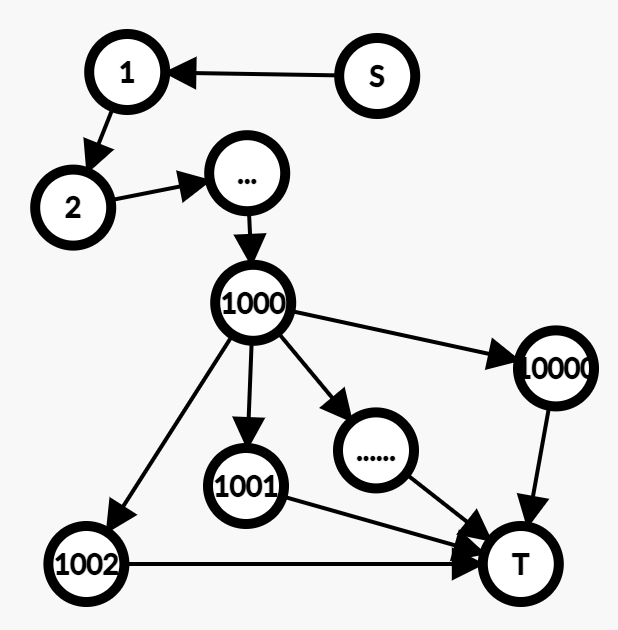
如果使用 EK 算法求解最大流，它会不停地走 \(S \to 1 \to 2 \to ... \to 1000 \to x \to T(10^3 < x \le 10^4)\) 这条路径，前面的链被重复走了很多次，效率低下。

我们能否走到 \(T\) 之后不是回到 \(S\)，而是回到 \(1000\)？想要实现回溯，就得使用 dfs。这里，我们采用 dfs（FF 算法）与 bfs（EK 算法）的结合体——Dinic 算法解决此类情形。

具体地，我们在每一轮寻找之前先进行一遍 bfs，确定每个点的「层数」（即源点到它的最短距离）。

在 dfs 中，我们只需要每次去到下一个节点的时候，保证层数严格递增即可实现同 EK 算法一样的效果。

同时，当我们走过一条边以后，要么它的流量被榨干了，要么我们自己的流量被榨干了，于是它完全没有了利用价值，下次应该从它的下一条边开始，从而优化效率。这被称为当前弧优化。

具体实现细节详见代码。

P3376

模板。

EK code

#include<bits/stdc++.h>
#define int long long
using namespace std;const int N=1e4+5;
int n,m,s,t;
int maxflow;
int inc[N],edge[N],to[N],pre[N];
bool vis[N];
struct EDGE{int v,w,i;
};
vector<EDGE> G[N];bool bfs(){memset(vis,0,sizeof vis);queue<int> q;vis[s]=1;inc[s]=0x3f3f3f3f;	q.push(s);while(!q.empty()){int cur=q.front();q.pop();for(auto nxt:G[cur]){if(edge[nxt.i]){if(vis[nxt.v])continue;inc[nxt.v]=min(inc[cur],edge[nxt.i]);pre[nxt.v]=nxt.i;vis[nxt.v]=1;q.push(nxt.v);if(nxt.v==t)return 1;}}}return 0;
}
void update(){maxflow+=inc[t];int cur=t;while(cur!=s){int last=pre[cur];edge[last]-=inc[t];edge[last^1]+=inc[t];cur=to[last^1];}
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cin>>n>>m>>s>>t;for(int i=0,u,v,w;i<2*m;i+=2){cin>>u>>v>>w;G[u].push_back({v,w,i});edge[i]=w,to[i]=v;G[v].push_back({u,w,i^1});to[i^1]=u;}while(bfs())update();cout<<maxflow;return 0;
}

Dinic code

#include<bits/stdc++.h>
#define int long long
using namespace std;const int N=1e4+5;
int n,m,s,t;
int maxflow,eid;
int edge[N],level[N],sta[N];
struct EDGE{int v,w,i;
};
vector<EDGE> G[N];void add(int u,int v,int w,int i){G[u].push_back({v,w,eid});edge[eid]=w,eid++;G[v].push_back({u,0,eid});edge[eid]=0,eid++;
}
bool bfs(){memset(level,0,sizeof level);queue<int> q;q.push(s);level[s]=1;while(!q.empty()){int cur=q.front();q.pop();sta[cur]=0;for(auto nxt:G[cur]){if(edge[nxt.i]&&!level[nxt.v]){level[nxt.v]=level[cur]+1;q.push(nxt.v);if(nxt.v==t)return 1;}}}return 0;
}
int dinic(int cur,int flow){if(cur==t)return flow;int rest=flow;for(int x=sta[cur];x<G[cur].size();x++){auto nxt=G[cur][x];sta[cur]=x;if(rest&&edge[nxt.i]&&level[nxt.v]==level[cur]+1){int inc=dinic(nxt.v,min(rest,edge[nxt.i]));if(!inc)level[nxt.v]=0;edge[nxt.i]-=inc;edge[nxt.i^1]+=inc;rest-=inc;}}return flow-rest;
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cin>>n>>m>>s>>t;for(int i=1,u,v,w;i<=m;i++){cin>>u>>v>>w;add(u,v,w,i);}while(bfs())maxflow+=dinic(s,0x3f3f3f3f);cout<<maxflow;return 0;
}

P2065

显然最大匹配是可以做的，不过会 T 飞。

看到这种匹配问题，考虑网络流建模。虚拟一个源点、汇点，将源点连蓝卡、蓝卡连红卡（要求 \(\gcd>1\)）、红卡连汇点，边权均为 \(1\)（不能重复使用），然后跑最大流即可。但还是 T 飞了。

容易发现，根本原因是边太多了（接近 25w 条），这显然是饥饿和 EK 都无法接受的。

考虑到两个数 \(\gcd >1\) 必定有公质因子，于是将每个数进行质因数分解，然后连向各自的质因子。因为数 \(<10^7\)，于是不同的质因子不会超过 \(10\) 个，这样点没增加多少，边却减少了很多。

code

//法二：网络流
#include<bits/stdc++.h>
#define int long long
using namespace std;const int N=1e4+5,M=1e5+5;
int T,n,m,s,t,ptot,maxflow,eid;
int inc[N],edge[M],to[M],pre[N],pid[M];
bool vis[N];
struct EDGE{int v,w,i;
};
vector<EDGE> G[N];void adde(int u,int v,int w){G[u].push_back({v,w,eid});edge[eid]=w,to[eid]=v,eid++;G[v].push_back({u,0,eid});edge[eid]=0,to[eid]=u,eid++;
}
void fuckit(int cur,int num,int typ){for(int i=2;i*i<=num;i++){if(num%i==0){while(num%i==0)num/=i;if(!pid[i])pid[i]=++ptot;if(!typ)adde(cur,n+m+pid[i],1);elseadde(n+m+pid[i],cur,1);}}if(num>1){if(!pid[num])pid[num]=++ptot;if(!typ)adde(cur,n+m+pid[num],1);elseadde(n+m+pid[num],cur,1);}
}
bool bfs(){memset(vis,0,sizeof vis);queue<int> q;vis[s]=1;inc[s]=0x3f3f3f3f;	q.push(s);while(!q.empty()){int cur=q.front();q.pop();for(auto nxt:G[cur]){if(edge[nxt.i]&&!vis[nxt.v]){inc[nxt.v]=min(inc[cur],edge[nxt.i]);pre[nxt.v]=nxt.i;vis[nxt.v]=1;q.push(nxt.v);if(nxt.v==t)return 1;}}}return 0;
}
void update(){maxflow+=inc[t];int cur=t;while(cur!=s){int last=pre[cur];edge[last]-=inc[t];edge[last^1]+=inc[t];cur=to[last^1];}
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cin>>T;while(T--){eid=0;for(int i=0;i<N;i++)G[i].clear();cin>>m>>n;for(int i=1;i<=m;i++)adde(s,i,1);memset(pid,0,sizeof pid);ptot=0;for(int i=1,x;i<=m;i++)cin>>x,fuckit(i,x,0);for(int i=1,x;i<=n;i++)cin>>x,fuckit(i+m,x,1);t=n+m+ptot+1;for(int i=1;i<=n;i++)adde(i+m,t,1);maxflow=0;memset(inc,0,sizeof inc);while(bfs())update();cout<<maxflow<<'\n';}return 0;
}

P2472

有限制条件且有路径，考虑网络流。又要求逃出去的最多，考虑最大流。

石柱的高度是限制条件，肯定得作边权，于是我们把一个格子拆成两个点（入点、出点）即可。

虚拟一个源点、汇点，源点连起点，边权 \(1\)（最多所有蜥蜴都逃出去）；每石柱入点连出点，边权为石柱高度；每个石柱的出点连和它距离不超过 \(d\) 的格子，边权为 \(\infty\)；每个石柱若它能跳出界外，则与汇点连边，边权为 \(\infty\)。

code

#include<bits/stdc++.h>
#define int long long
using namespace std;const int N=1e3+5,M=1e5+5;
const int INF=0x3f3f3f3f;
int r,c,s,t,d;
int tots,maxflow,eid;
int edge[M],sta[N],level[N];
int h[N][N];
char mp[N][N];
struct EDGE{int v,w,i;
};
vector<EDGE> G[N];
int st[N];int get(int x,int y){return (x-1)*c+y;
}
int get_dis(int x,int y,int xx,int yy){return (x-xx)*(x-xx)+(y-yy)*(y-yy);
}
void add(int x,int y,int w){G[x].push_back({y,w,eid});edge[eid]=w,eid++;
}
bool bfs(){memset(level,0,sizeof level);queue<int> q;level[s]=1;q.push(s);while(!q.empty()){int cur=q.front();sta[cur]=0;q.pop();for(auto nxt:G[cur]){if(edge[nxt.i]&&!level[nxt.v]){level[nxt.v]=level[cur]+1;q.push(nxt.v);if(nxt.v==t)return 1;}}}return 0;
}
int dinic(int cur,int flow){if(cur==t)return flow;int rest=flow;for(int i=sta[cur];i<G[cur].size();i++){auto nxt=G[cur][i];sta[cur]=i;if(rest&&edge[nxt.i]&&level[nxt.v]==level[cur]+1){int inc=dinic(nxt.v,min(edge[nxt.i],rest));if(!inc)level[nxt.v]=0;edge[nxt.i]-=inc;edge[nxt.i^1]+=inc;rest-=inc;}}return flow-rest;
}signed main(){ios::sync_with_stdio(0);cin.tie(0);cin>>r>>c>>d;for(int i=1;i<=r;i++){for(int j=1;j<=c;j++){char ch;cin>>ch,h[i][j]=ch-'0';}}for(int i=1;i<=r;i++){for(int j=1;j<=c;j++){cin>>mp[i][j];if(mp[i][j]=='L')st[++tots]=get(i,j);}}for(int i=1;i<=tots;i++)add(s,st[i],1),add(st[i],s,0);for(int i=1;i<=r;i++)for(int j=1;j<=c;j++)for(int ii=1;ii<=r;ii++)for(int jj=1;jj<=c;jj++)if((i!=ii||j!=jj)&&h[i][j]&&h[ii][jj]&&get_dis(i,j,ii,jj)<=d*d)add(get(i,j)+r*c,get(ii,jj),INF),add(get(ii,jj),get(i,j)+r*c,0);for(int i=1;i<=r;i++)for(int j=1;j<=c;j++)if(h[i][j])add(get(i,j),get(i,j)+r*c,h[i][j]),add(get(i,j)+r*c,get(i,j),0);t=2*r*c+1;for(int i=1;i<=r;i++)for(int j=1;j<=c;j++)if(h[i][j]&&(j<=d||c-j+1<=d||i<=d||r-i+1<=d))add(get(i,j)+r*c,t,INF),add(t,get(i,j)+r*c,0);while(bfs())maxflow+=dinic(s,INF);cout<<tots-maxflow;return 0;
}

总结：