信息量，熵，交叉熵，相对熵的定义

news/2025/1/19 18:50:37/文章来源:https://www.cnblogs.com/gongzb/p/18679802

本文将介绍信息量，熵，交叉熵，相对熵的定义，以及它们与机器学习算法中代价函数的定义的联系。转载请保留原文链接：http://www.cnblogs.com/llhthinker/p/7287029.html

1. 信息量

信息的量化计算：

解释如下：

信息量的大小应该可以衡量事件发生的“惊讶程度”或不确定性：

如果有⼈告诉我们⼀个相当不可能的事件发⽣了，我们收到的信息要多于我们被告知某个很可能发⽣的事件发⽣时收到的信息。如果我们知道某件事情⼀定会发⽣，那么我们就不会接收到信息。也就是说，信息量应该连续依赖于事件发生的概率分布p(x) 。因此，我们想要寻找⼀个基于概率p(x)计算信息量的函数h(x)，它应该具有如下性质：

h(x) >= 0，因为信息量表示得到多少信息，不应该为负数。
h(x, y) = h(x) + h(y)，也就是说，对于两个不相关事件x和y，我们观察到两个事件x, y同时发⽣时获得的信息应该等于观察到事件各⾃发⽣时获得的信息之和；
h(x)是关于p(x)的单调递减函数，也就是说，事件x越容易发生（概率p(x)越大），信息量h(x)越小。

又因为如果两个不相关事件是统计独⽴的，则有p(x, y) = p(x)p(y)。根据不相关事件概率可乘、信息量可加，很容易想到对数函数，看出h(x)⼀定与p(x)的对数有关。因此，有

满足上述性质。

2. 熵（信息熵）

对于一个随机变量X而言，它的所有可能取值的信息量的期望

连续变量：

3. 交叉熵

现有关于样本集的2个概率分布p和q，其中p为真实分布，q非真实分布。按照真实分布p来衡量识别一个样本的熵，即基于分布p给样本进行编码的最短平均编码长度为：

如果使用非真实分布q来给样本进行编码，则是基于分布q的信息量的期望（最短平均编码长度），由于用q来编码的样本来自分布p，所以期望与真实分布一致。所以基于分布q的最短平均编码长度为：

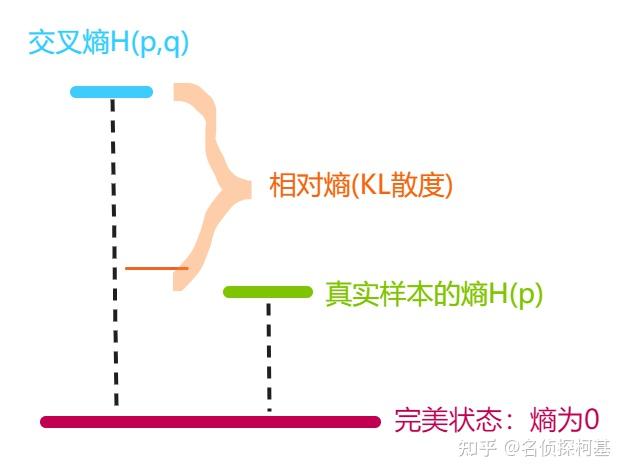
上式CEH(p, q)即为交叉熵的定义。

4. 相对熵

将由q得到的平均编码长度比由p得到的平均编码长度多出的bit数，即使用非真实分布q计算出的样本的熵(交叉熵)，与使用真实分布p计算出的样本的熵的差值，称为相对熵，又称KL散度。

KL(p, q) = CEH(p, q) - H(p)=

相对熵（KL散度）用于衡量两个概率分布p和q的差异。注意，KL(p, q)意味着将分布p作为真实分布，q作为非真实分布，因此KL(p, q) != KL(q, p)。

5. 机器学习中的代价函数与交叉熵

若 $p(x)$ 是数据的真实概率分布， $q(x)$ 是由数据计算得到的概率分布。机器学习的目的就是希望 $q(x)$ 尽可能地逼近甚至等于 $p(x)$ ，从而使得相对熵接近最小值0. 由于真实的概率分布是固定的，相对熵公式的后半部分（-H(p)）就成了一个常数。那么相对熵达到最小值的时候，也意味着交叉熵达到了最小值。对 $q(x)$ 的优化就等效于求交叉熵的最小值。另外，对交叉熵求最小值，也等效于求最大似然估计（maximum likelihood estimation）。

特别的，在logistic regression中，
p:真实样本分布，服从参数为p的0-1分布，即