训练情况
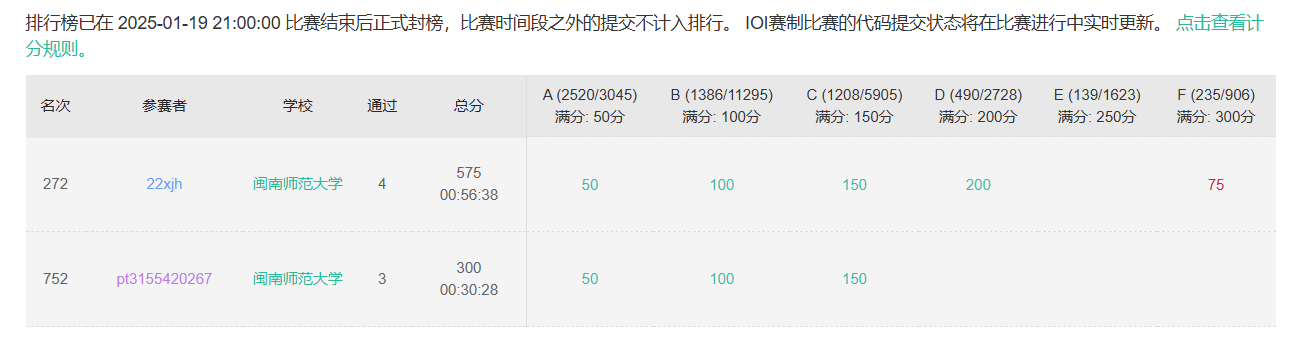
赛后反思
打一半吃饭去了,C题看到 ax+by=k 的问题,简单的扩欧exgcd没反应过来,简单数论还是不熟悉TAT,D题DSU计算联通块大小时 \(i\) 打成 \(a_i\) 疯狂 RE 被硬控了十几分钟
A题
输出题目所述的第几个字符串即可
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){string s[7] = {"","20250121","20250123","20250126","20250206","20250208","20250211"};int x; cin>>x;cout<<s[x]<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
B题
记录 \(1 \sim 9\) 的出现次数,如果出现次数最大值与最小值的差超过 \(2\) 就必定无法成为数独,因为会多两个相同的数字
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;vector<int> a(n + 1);vector<int> cnt(10);for(int i = 1;i<=n;i++) cin>>a[i],cnt[a[i]]++;bool flag = true;int ma = 0,mi = INT_MAX;for(int i = 1;i<=9;i++){ma = max(ma,cnt[i]);mi = min(mi,cnt[i]);}if(ma-mi<=1) cout<<"YES"<<endl;else cout<<"NO"<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
C题
我们将 x,y 轴分开考虑
向右d向左c可以等价看成两种操作 +d 和 +(d-c),这两种操作是否存在 \((x,y)\) 使得 ax + by = 终点横坐标
向上a向下b可以等价看成两种操作 +a 和 +(a-b),这两种操作是否存在 \((x,y)\) 使得 ax + by = 终点纵坐标
我们使用扩展欧几里得 exgcd 判断是否存在合法解即可
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;int x,y;int exgcd(int a,int b){if(b==0){x=1;y=0;return a;}int d=exgcd(b,a%b);int t=x;x=y;y=t-a/b*y;return d;
}void solve(){int x,y,a,b,c,d;cin>>x>>y>>a>>b>>c>>d;int e = exgcd(d-c,d);int f = exgcd(a-b,a);if(x%e||y%f) cout<<"NO"<<endl;else cout<<"YES"<<endl;
}signed main(){int T; cin>>T; while(T--)solve();return 0;
}
D题
二进制+并查集,我们只要维护每一位 \(1\) 上面的元素个数即可,所以我这边采用 n + 1 + j 表示二进制第 j 位为 1,对于每个 \(a_i\) 转为二进制使用并查集维护即可,最后统计最大的联通块即可
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;const int N = 2e5;int a[N],cnt[N],fa[N];int Find(int x){if(fa[x] == x) return x;return fa[x] = Find(fa[x]);
}void Union(int x,int y){x = Find(x); y = Find(y);if(x == y) return;fa[y] = x;
}void solve(){int n; cin>>n;for(int i = 1;i<=n+100;i++) fa[i] = i,cnt[i] = 0;for(int i = 1;i<=n;i++) cin>>a[i];for(int i = 1;i<=n;i++){for(int j = 63;~j;j--){if((1ll<<j)&a[i]) Union(i,n+j+1);}}for(int i = 1;i<=n;i++) cnt[Find(i)]++;int ans = 0;for(int i = 1;i<=n;i++) ans = max(ans,cnt[i]);cout<<ans<<endl;
}signed main(){int T; cin>>T; while(T--)solve();return 0;
}