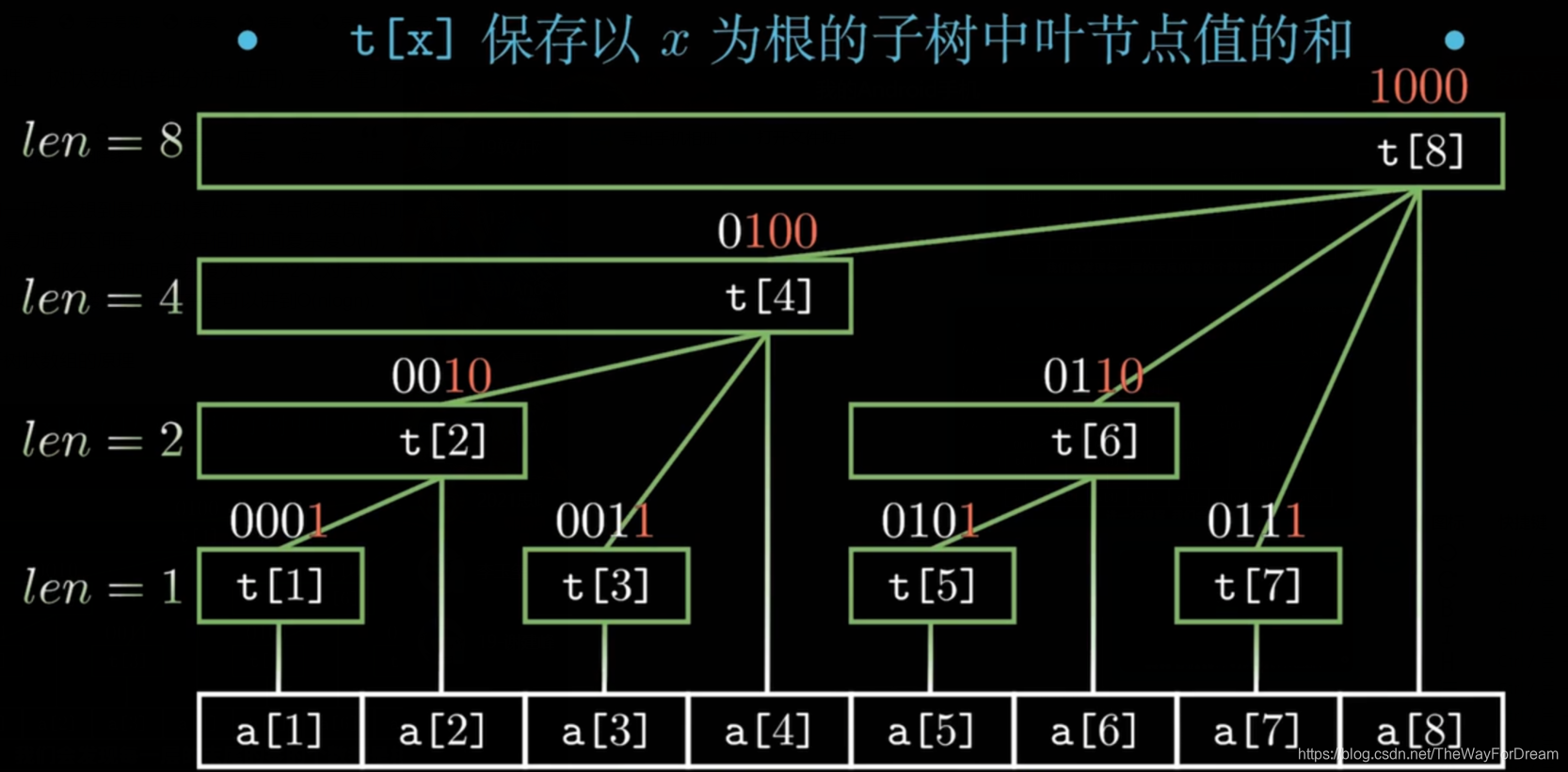
2025 刷题计划 - 线段树

news/2025/1/20 20:38:56/文章来源:https://www.cnblogs.com/laoshan-plus/p/18682494

2025 刷题计划 - 线段树

A. P3313 [SDOI2014] 旅行

树剖板子题，开 \(C\) 棵线段树即可。你可能会说开不下？动态开点不就完了。

B. P3924 康娜的线段树

有意思的一道题，貌似 \(O(n\log n)\) 解法比 \(O(n)\) 更难？我实现不出来。

首先易得期望的计算方式即为：设当前节点 \(x\) 的深度为 \(\text{dep}(x)\)，则访问它的概率就是 \(\dfrac1{2^{\text{dep}(x)}}\)，最朴素的期望计算方式就是概率乘上线段树上节点的数值并全部加起来。考虑怎么优化这样一个过程，我们不能通过建树来求每个节点的值，考虑计算每个节点的贡献。易得每个叶子节点的贡献为 \(a_x\times\sum\limits_{i=0}^{\text{dep}(x)}\dfrac1{2^{\text{dep}(x)-i}}=a_x\times\left(2-\dfrac1{2^{\text{dep}(x)}}\right)\)。显然每个节点的 \(\text{dep}\) 值都是确定的，所以我们可以一遍 \(O(n)\) 计算出最初的答案。

当遇到区间加的修改时，答案增大了 \(x\times\sum\limits_{i=l}^r\left(2-\dfrac1{2^{\text{dep}(i)}}\right)\)。通过维护 \(2-\dfrac1{2^{\text{dep}(i)}}\) 的前缀和即可 \(O(1)\) 回答所有询问。

具体实现的时候不需要 \(\tt double\)，只需要乘上一个数最后再除回去即可。因为题目保证答案乘上 \(\mathit{qwq}\) 是整数，所以这样做是可行的。只需判断需不需要开 \(\tt\_\_int128\)。

C. P4243 [JSOI2009] 等差数列

很好的线段树练习题。

首先维护等差数列容易想到维护差分序列。那么差分后，等差数列就转化为给差分数列的两个单修和一个区修。考虑怎么统计答案，通过线段树维护区间最大子段和的套路，用 \(s_{0/1/2/3}\) 分别维护左右端点都不包含、包含左、包含右、左右都包含的最小划分数。重点在于 pushup，这里要注意一定是把左右儿子的包含左、包含右合并到都不包含或者都包含，不需要重复地把都不包含进行合并。结合代码理解会好一点。

friend SegTree operator+(const SegTree&x,const SegTree&y){SegTree res;res.l=x.l,res.r=y.r;bool fl=x.r==y.l;res.s[0]=min({x.s[2]+y.s[1]-fl,x.s[0]+y.s[1],y.s[0]+x.s[2]});res.s[1]=min({x.s[1]+y.s[1],x.s[3]+y.s[0],x.s[3]+y.s[1]-fl});res.s[2]=min({y.s[2]+x.s[2],y.s[3]+x.s[0],y.s[3]+x.s[2]-fl});res.s[3]=min({x.s[1]+y.s[3],y.s[2]+x.s[3],x.s[3]+y.s[3]-fl});return res;
}

注意结构体需要写构造函数进行初始化！

另外，差分数组我们只考虑 \([2,n]\) 的区间，因为第一位是和 \(0\) 进行差分，没有意义。

D. P1545 [USACO04DEC] Dividing the Path G

一个区间左右喷灌很不好处理，考虑把它转化为只向左喷灌，把喷灌区间 \(\times2\) 即可处理。原题中的 “奶牛指定区间只能由一个喷灌器喷灌” 可以转化为区间内部不能放置喷灌器，打标记即可。最后一个暴力 DP 就出来了。~~然后这题你就愉快地水过去了。~~

转移方程：\(f_i=\min\{f_j\}+1\)。

正解当然是线段树优化 DP，主要是优化了区间取最小值的过程。~~跑得还没暴力快。~~

E. CF1975E Chain Queries

看似一眼题的一道树剖题。做法很多。

一种比较简单的做法是找全部黑点成为一条链的性质。易得（？的性质是：

如果全部黑点成为一条链，则试统计没有儿子是黑点的黑点个数，记为 \(\mathit{cnt}\)。若 \(\mathit{cnt}=1\)，直接输出 Yes（此时所有黑点必定成链且链的一端是所有黑点的祖先）；若 \(\mathit{cnt}=2\)，将两点记为 \(x,y\)，则形成一条路径当且仅当 \(x\to y\) 的路径的黑点数量等于 \(\operatorname{dis}(x,y)+1\)；若 \(\mathit{cnt}>2\) 必定是 No。