例题一:P3374 【模板】树状数组 1
例题二:P3368 【模板】树状数组 2
作用:
- 特征: 一个多用于区间修改,和单点查询。或区间查询单点修改的数据结构,其代码量较少,比较好写。
- 区别: 它与线段树的功能差不多,但线段树的可拓展性更强。也就是说:树状数组能做的,线段树都能做;而线段树能做的,树状数组有些不能做。但树状数组都可以被线段树替代,那还学什么树状数组?理由很简单它的常数小,且码量小,考场上线段树要写半个小时,而树状数组只需要十几分钟。
- 优缺点: 总结下来,线段树有一下缺点:
\(1.\)拓展性小
\(2.\)对区间维护的值有较高的要求:普通树状数组维护的信息及运算要满足 结合律 且 可差分,如加法(和)、乘法(积)、异或等。
- 结合律:\((x \circ y) \circ z = x \circ (y \circ z)\),其中 \(\circ\) 是一个二元运算符。
- 可差分:具有逆运算的运算,即已知 \(x \circ y\) 和 \(x\) 可以求出 \(y\)。
优点也很明显:
\(1.\)码量小
\(2.\)常数小
\(3.\)好调试
实现:
基本模型:
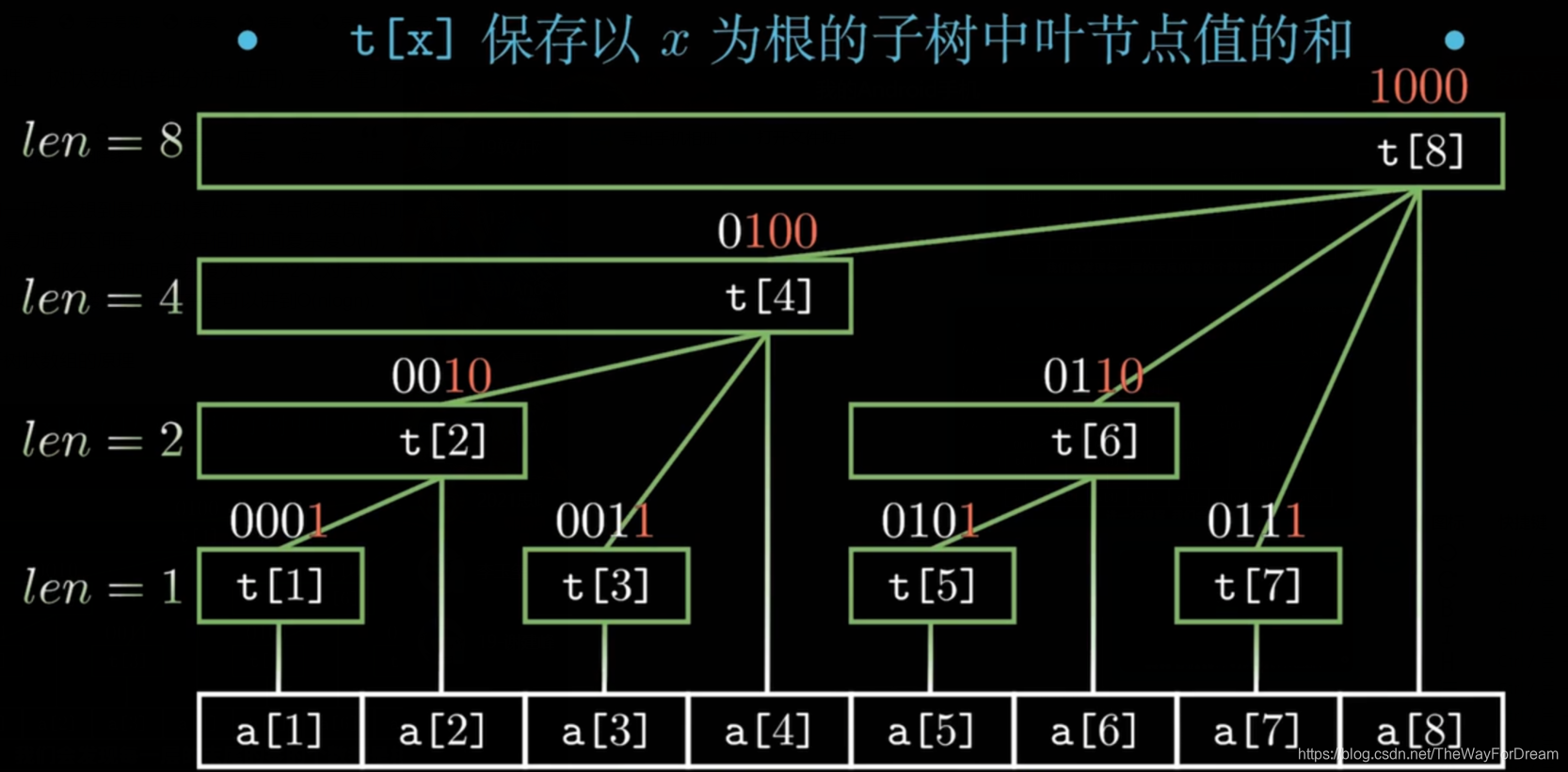
\(2.\)我们先给出一个基本概念 —— \(lowbit\)
\(lowbit\) 指该数二进制下从右往左第一个 \(1\) 的位置的值,如 \(6\) 二进制下 \((6)_{10}=(110)_2\),那它的的\(lowbit\) 值就是 \(10\) ,在比如\((664)_{10}=(1010011000)_2\),则 \(lowbit(664)=(1000)_2\)
那如何求 \(lowbit\),我们知道,在计算机中,一个负数的等于它正数的二进制全部取反在加 \(1\),及假设有一二进制正数 \((1010011000)_2\) 则全部取反后为 \((0101100111)_2\) 在加一就变为 \((0101101000)\) 这时就发现当前数的 \(lowbit\) 就是和它负数的与,及 \(lowbit(x)=x \& -x\)。原理也很简单,因为第一个 \(1\) 前的所有 \(0\) 都变为一,而加一就会全部进位,重新变回 \(0\) 而 \(1\)会变成 \(0\) 所有进位到这就停止了,所以第一个 \(1\) 后的就会变成一样的,其他就不同
int lowbit(int x){return x&(-x);
}
\(3.\)知道了 \(lowbit\) 的概念后在看树状数组的基本样子,我们发现,任意一个节点的父亲节点的编号都等于该节点的编号加 \(lowbit\) ,及 \(fa_x=x+lowbit(x)\) 而我们每个节点的值都对应储存了某一个区间的值(后面以区间和为例),那我们又该如何找到对应的区间了?
\(4.\)我们发现一个区间的下一个包含最多区间的节点编号为 该节点编号减去其 \(lowbit\)值,及 \(x-lowbit(x)\),原因很简单,因为树状数组上的每个节点的 \(lowbit\)值就是它所代表区间的长度。
操作:
知道了这最基本的几个性质后,就好进行操作了:
区间查询和单点修改:
\(1.\)单点修改: 我们只需要修改根节点的值并逐步向上递推,依次修改所有父亲节点,时间复杂度 \(O(logn)\)
void add(int x,int num){for(int i=x;i<=n;i+=lowbit(i)){t[i]+=num;}
}
\(2.\)建树: 对于每个点都进行加点即可,时间复杂度 \(O(nlogn)\)
\(3.\)区间查询: 我们要查询 \(l\)到\(r\)的区间和,它实际上就相当于找到 \(1 \sim r\) 的区间和,在减去 \(1 \sim l-1\)的区间和,只需要循环加上每个区间的和即可:
int query(int l,int r){int res=0;for(int i=r;i>=1;i-=lowbit(i)){res+=t[i];}for(int i=l-1;i>=1;i-=lowbit(i)){res-=t[i];}return res;
}
区间修改和单点修改:
\(1.\)区间修改: 若暴力修改每一个点,那复杂度为 \(O(nlogn)\)比较劣,但我们考虑差分,差分可以将一个区间的修改改为对两个点的修改,这样只需要对 \(l\) 加上修改值,对 \(r+1\) 减去修改值即可:
add(l,k);
add(r+1,-k);void add(int x,int num){for(int i=x;i<=n;i+=lowbit(i)){t[i]+=num;}
}
\(1.\)单点查询: 由于维护的是差分,所以一个点的值等于差分数组的前缀和,只需要不断跳即可:
int query(int r){int res=0;for(int i=r;i>=1;i-=lowbit(i)){res+=t[i];}return res;
}
第一题完整代码:
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int a[N];
int n,m;
int lowbit(int x){return x&(-x);
}
int t[2*N];
void add(int x,int num){for(int i=x;i<=n;i+=lowbit(i)){t[i]+=num;}
}
int query(int l,int r){int res=0;for(int i=r;i>=1;i-=lowbit(i)){res+=t[i];}for(int i=l-1;i>=1;i-=lowbit(i)){res-=t[i];}return res;
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];add(i,a[i]);}for(int i=1;i<=m;i++){int op;cin>>op;if(op==1){int x,k;cin>>x>>k;add(x,k);}else if(op==2){int x,y;cin>>x>>y;cout<<query(x,y)<<endl;}}
}
第二题完整代码:
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int lowbit(int x){return x&(-x);
}
int a[N],t[2*N];
int n,m;
void add(int x,int num){for(int i=x;i<=n;i+=lowbit(i)){t[i]+=num;}
}
int query(int r){int res=0;for(int i=r;i>=1;i-=lowbit(i)){res+=t[i];}return res;
}
int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];int num=a[i]-a[i-1];add(i,num);}for(int i=1;i<=m;i++){int op;cin>>op;if(op==1){int x,y,k;cin>>x>>y>>k;add(x,k);add(y+1,-k);}else if(op==2){int x;cin>>x;cout<<query(x)<<endl;}}
}