树上的轮廓线DP！——AGC017F Zigzag

树上的轮廓线DP！——AGC017F Zigzag

注意到 \(n,m\le 20\)，考虑状压，设 \(f_{i,S}\) 表示对于第 \(i\) 条线，其路线为 \(S\) 的方案数。

转移需要枚举 \(f_{i-1,S'}\) 复杂度 \(\mathcal O(4^n\text{poly}(n))\)。

发现这种相邻状态之间的限制很像矩形中行的扩展，于是我们可以考虑类似的方法，使用轮廓线DP。

设 \(f_{i,j,S}\) 表示处理到了第 \(i\) 条路径并走到第 \(j\) 层， \(S_{0\sim j-1}\) 表示 第 \(i\) 条路径的行走方案， \(S_{j\sim n-1}\) 表示第 \(i-1\) 条路径的行走方案。由于这只能知道 \(i-1\) 的相对自己原位置的变换，所以还要记录一个 \(dis\) 表示 \(i-1,i\) 之间的距离，即状态为 \(f_{i,j,S,dis}\)。复杂度 \(\mathcal O(2^nn^2m)\)。

考虑进一步优化， \(i,j\) 都是阶段，不能去掉，但 \(S\) 与 \(dis\) 去共同起到限制作用，能不能合并为一起限制呢？考虑精确限制。

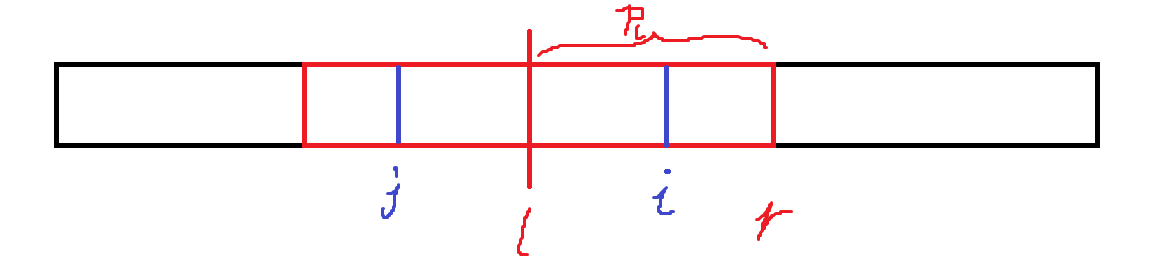
如图，假设第 \(i-1\) 条路径的限制为绿色，而 \(i\) 决定向右走（即红色）,那么 \(i\) 能到达的区域就是蓝色线条围成的三角形，最终可以到的地方就是蓝色与绿色限制的交集，我们直接用 \(S_{j\sim n-1}\) 维护可以到的左边界即可。具体方法就是将绿色的先下移，再说具体点就是把 \(S_{j\sim n-1}\) 的第一个 \(1\) （向右走）提到最开头。复杂度 \(\mathcal O(2^nnm)\)。