论建边

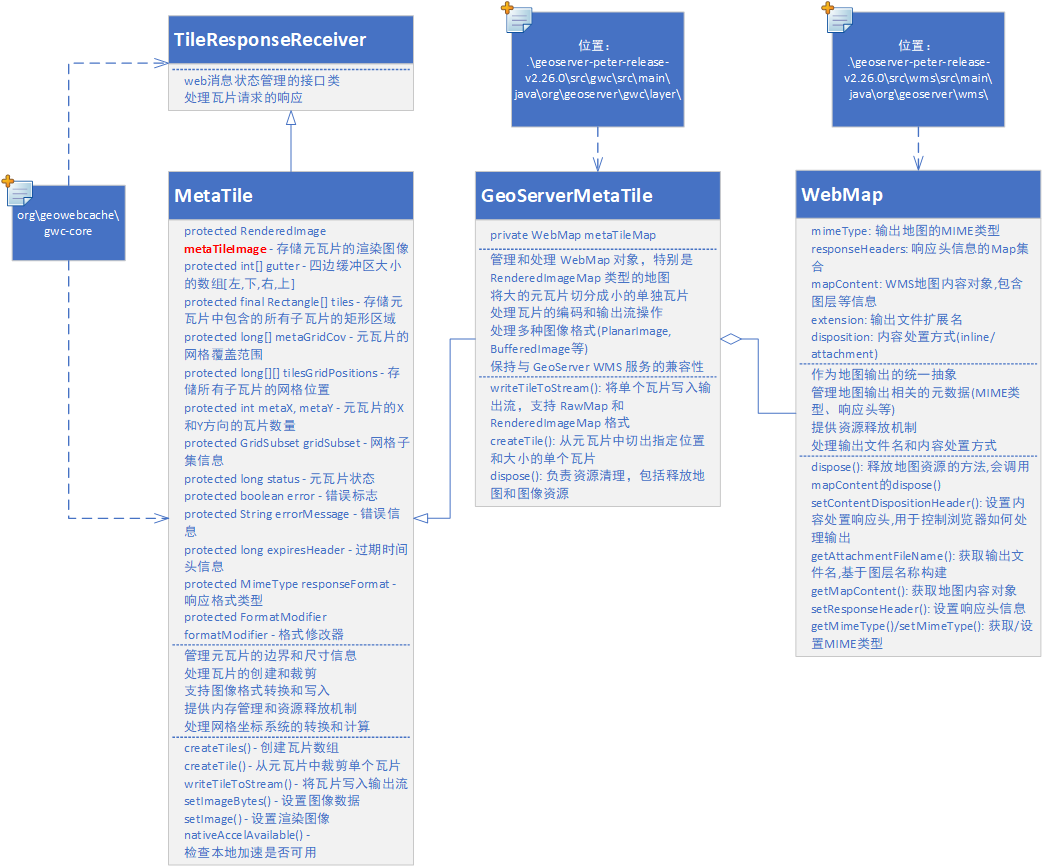
# 论建边图论中的边用于连接两个节点。若是要抽象建图，则也应该找到二元关系，即“边”。这里举几个例子：[P10350 [PA2024] Modernizacja Bajtocji]([P10350 [PA2024] Modernizacja Bajtocji - 洛谷 | 计算机科学教育新生态](https://www.luogu.com.cn/problem/P10350))我们发现他将将电脑送给 $a_i,b_i$ 二选一，所以可以考虑连 $a_i,b_i$ 无向边。具体根据题目性质使用并查集[[[AGC017E] Jigsaw](https://www.luogu.com.cn/problem/AT_agc017_e)我们首先的一个想法是把两个可以连接的拼图之间连边，但是这样需要做一个不经过重复点的有向图路径覆盖，行不通。我们发现一个拼图也同时将其左右两个高度绑定在一起，所以可以考虑将高度作为点，拼图作为边，由于左右顺序相关，所以应该连有向边，这样就变为了一个不经过重复边的有向图路径覆盖，这是可以的。这也告诉我们有些时候可以点边转化解决问题。具体连边方式如下：> 利用正负性区分左右 > 对于一个拼图左边，接地为 $a_i$，否则为 $-c_i$ > 对于右边，接地为 $-b_i$，否则为 $d_i$ > 然后左边连右边 > > 设置正负以后，巧妙地保证了右连左，并且权值相同的正好表示可以拼起来 > 问题变为将边集分为若干条边不交路径，要求起点正，终点负 > 换句话说，正点出度$>$入度，负点入度$>$出度还有一点小问题，可能连成环 > 其实只要联通块内存在入度不等于出度的点即可