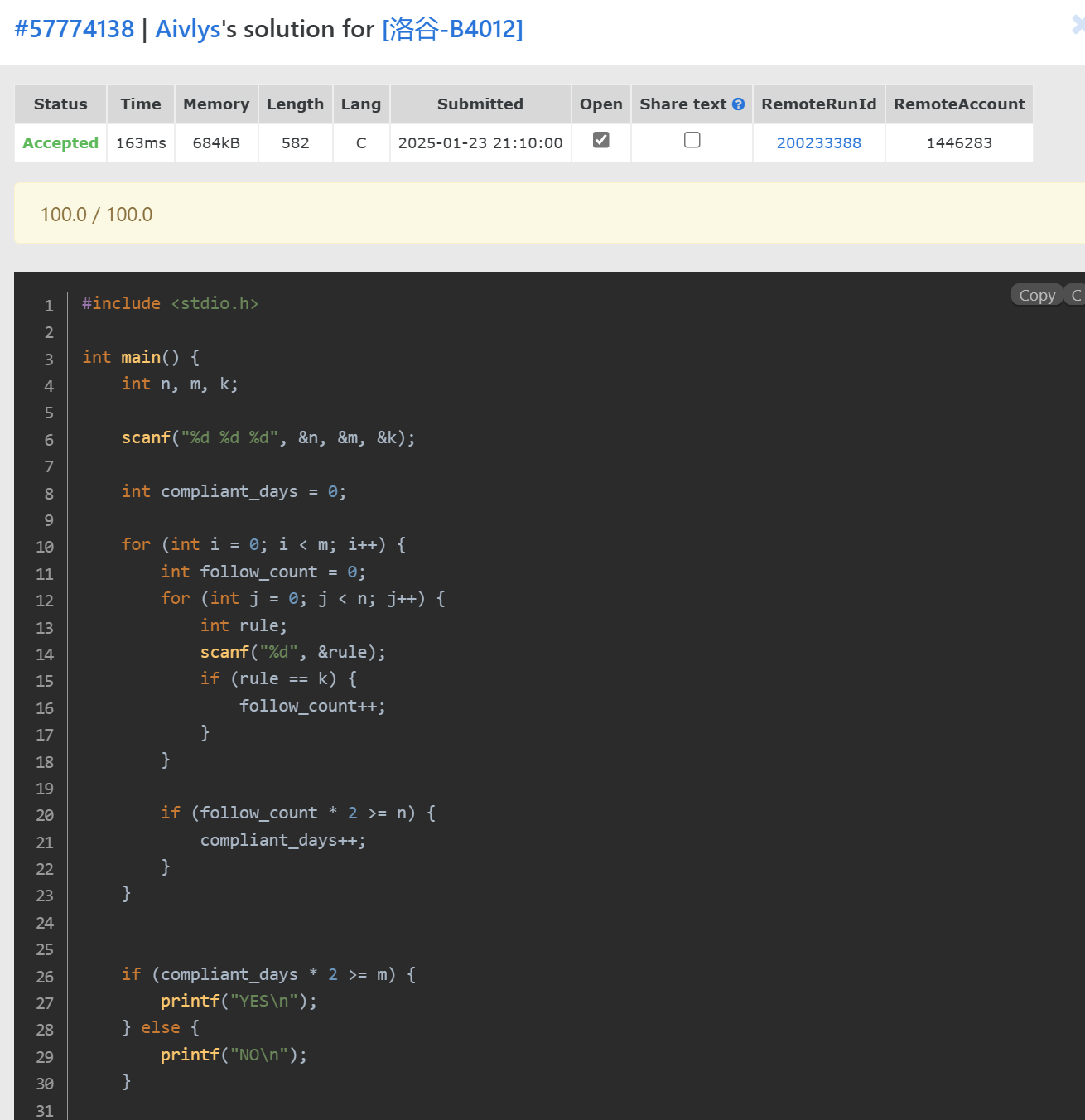
题目:P1470 [USACO2.3] 最长前缀 Longest Prefix
题目解析
问题描述
给定一个元素集合 ( P ) 和一个大写字母序列 ( s ),要求找到 ( s ) 的最长前缀 ( s' ),使得 ( s' ) 可以由 ( P ) 中的元素组成。元素可以重复使用,但不一定要全部出现。
解题思路
- 输入处理:
- 读取元素集合 ( P ),并将其按长度存储在不同的
set中。 - 读取大写字母序列 ( s ),并将其拼接成一个连续的字符串。
- 读取元素集合 ( P ),并将其按长度存储在不同的
- 动态规划:
- 使用一个动态规划数组
dp,其中dp[i]表示前i个字符的前缀是否可以由 ( P ) 中的元素组成。 - 初始化
dp[0] = 1,表示空前缀是合法的。 - 对于每个位置
i,从i向前查找长度不超过 ( m ) 的子串tt,检查tt是否存在于集合s[tt.size()]中,并且dp[i - tt.size()]是否为1。 - 如果上述条件满足,则更新
dp[i] = 1,并记录当前前缀的长度ans。
- 使用一个动态规划数组
- 输出结果:
- 输出
ans,即最长合法前缀的长度。
- 输出
代码实现
#include <iostream>
#include <set>
#include <cstring>
using namespace std;
int dp[200005], m;
set<string> s[20];
int main() {string tp;while (cin >> tp) {if (tp == ".") break;s[tp.size()].insert(tp); // 存到他大小的集合中m = max(m, int(tp.size()));}int i, ans = 0;dp[0] = 1; // 初始化string n;n = " ";while (cin >> tp) {n = n + tp; // 将所有的串合成一个}for (i = 1; i < n.size(); i++) { // 枚举子串for (int j = min(i, m); j >= 1; j--) {string tt = n.substr(i - j + 1, j); // 截除子串if (s[tt.size()].count(tt) == 1 && dp[i - j] == 1) { // 如果合法ans = i; // 必定是最大的dp[i] = 1; // 本身也合法break; // 没必要搜下去了}}}cout << ans;return 0;
}
代码解释
- 输入处理:
while (cin >> tp)读取元素集合 ( P ),直到遇到.。s[tp.size()].insert(tp)将每个元素按长度存储在对应的set中。m = max(m, int(tp.size()))记录集合中元素的最大长度。
- 动态规划数组初始化:
dp[0] = 1,表示空前缀是合法的。
- 读取并处理大写字母序列 ( s ):
n = " "初始化一个空字符串,用于拼接输入的多行字符串。while (cin >> tp)读取多行字符串,并将其拼接成一个连续的字符串n。
- 动态规划状态转移:
for (i = 1; i < n.size(); i++)从第 1 个字符开始,逐个字符处理。for (int j = min(i, m); j >= 1; j--)从当前位置i向前查找长度不超过m的子串tt。string tt = n.substr(i - j + 1, j)截取子串tt。if (s[tt.size()].count(tt) == 1 && dp[i - j] == 1)检查tt是否存在于集合s[tt.size()]中,并且dp[i - j]是否为1。ans = i更新最长合法前缀的长度。dp[i] = 1标记当前前缀为合法。break退出内层循环,避免不必要的检查。
- 输出结果:
cout << ans输出最长合法前缀的长度。
示例解析
为了更好地理解这个算法,我们可以通过图解来分析动态规划的过程。假设我们有以下输入:
输入:
A AB BA CA BBC
.
ABABACABAABC
1. 输入处理
首先,我们读取元素集合 P 并将其存储在 set 中,按长度分类:
s[1]存储长度为 1 的元素:{A}s[2]存储长度为 2 的元素:{AB, BA}s[3]存储长度为 3 的元素:{CA}s[4]存储长度为 4 的元素:{BBC}
最大长度m为 4。
2. 初始化动态规划数组
dp[0] = 1,表示空前缀是合法的。
3. 读取并处理大写字母序列 s
将输入的多行字符串拼接成一个连续的字符串 n:
n = " ABABACABAABC"
4. 动态规划状态转移
我们从第 1 个字符开始,逐个字符处理,尝试找到最长的合法前缀。
位置 1: n[1] = 'A'
- 检查
n[1:1]是否在s[1]中:A存在。 dp[0] = 1,所以dp[1] = 1。ans = 1。
位置 2: n[2] = 'B'
- 检查
n[2:2]是否在s[1]中:B不存在。 - 检查
n[1:2]是否在s[2]中:AB存在。 dp[0] = 1,所以dp[2] = 1。ans = 2。
位置 3: n[3] = 'A'
- 检查
n[3:3]是否在s[1]中:A存在。 dp[2] = 1,所以dp[3] = 1。ans = 3。
位置 4: n[4] = 'B'
- 检查
n[4:4]是否在s[1]中:B不存在。 - 检查
n[3:4]是否在s[2]中:BA存在。 dp[2] = 1,所以dp[4] = 1。ans = 4。
位置 5: n[5] = 'A'
- 检查
n[5:5]是否在s[1]中:A存在。 dp[4] = 1,所以dp[5] = 1。ans = 5。
位置 6: n[6] = 'C'
- 检查
n[6:6]是否在s[1]中:C不存在。 - 检查
n[5:6]是否在s[2]中:AC不存在。 - 检查
n[4:6]是否在s[3]中:CAB不存在。 - 检查
n[3:6]是否在s[4]中:BAC不存在。 dp[6] = 0,ans保持为 5。
位置 7: n[7] = 'A'
- 检查
n[7:7]是否在s[1]中:A存在。 dp[6] = 0,所以dp[7] = 0。- 检查
n[6:7]是否在s[2]中:CA存在。 dp[5] = 1,所以dp[7] = 1。ans = 7。
位置 8: n[8] = 'B'
- 检查
n[8:8]是否在s[1]中:B不存在。 - 检查
n[7:8]是否在s[2]中:AB存在。 dp[6] = 0,所以dp[8] = 0。- 检查
n[6:8]是否在s[3]中:CAB不存在。 - 检查
n[5:8]是否在s[4]中:BAC不存在。 dp[8] = 0,ans保持为 7。
位置 9: n[9] = 'A'
- 检查
n[9:9]是否在s[1]中:A存在。 dp[8] = 0,所以dp[9] = 0。- 检查
n[8:9]是否在s[2]中:AB存在。 dp[7] = 1,所以dp[9] = 1。ans = 9。
位置 10: n[10] = 'A'
- 检查
n[10:10]是否在s[1]中:A存在。 dp[9] = 1,所以dp[10] = 1。ans = 10。
位置 11: n[11] = 'B'
- 检查
n[11:11]是否在s[1]中:B不存在。 - 检查
n[10:11]是否在s[2]中:AB存在。 dp[9] = 1,所以dp[11] = 1。ans = 11。
位置 12: n[12] = 'C'
- 检查
n[12:12]是否在s[1]中:C不存在。 - 检查
n[11:12]是否在s[2]中:BC不存在。 - 检查
n[10:12]是否在s[3]中:ABC不存在。 - 检查
n[9:12]是否在s[4]中:ABBC不存在。 dp[12] = 0,ans保持为 11。
5. 输出结果
最终,最长的合法前缀长度为 11。
图解
我们可以用一个表格来表示 dp 数组的变化:
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | A | B | A | B | A | C | A | B | A | A | B | C | |
| dp | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| ans | 0 | 1 | 2 | 3 | 4 | 5 | 5 | 7 | 7 | 9 | 10 | 11 | 11 |