CTS2025Day1T1 倾诉

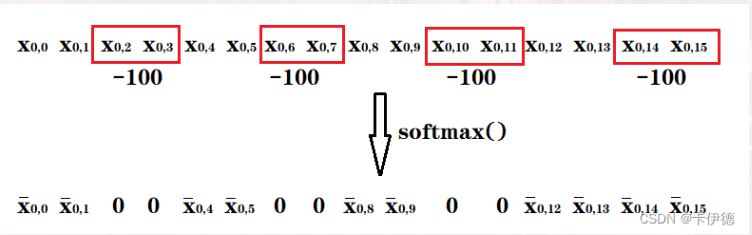
以下定义 \(lim=\lceil\log a\rceil\)。

首先结构一定是形如将整个序列划分成若干子段，形如 \((l,r,p)\) 的结构，其中 \(p\ge r\)，并且 \(p\) 严格单调递增，那么这一段的操作次数就是 \(p-l\)，不妨令 \(f(l,r,p)\) 表示对应的权值。由于 \(a_n\ge 1\)，所以说明最后一段的权值一定 \(\ge 1\)。所以我们可以说明一定存在一组解，满足 \(p-r\le lim\)，因为否则我们让 \(p\) 减小 \(1\)，则这一个段的权值依旧 \(<1\)，同时还节省了 \(1\) 次操作次数，并且仍然满足 \(p\) 单调递增的限制，于是 \((p,r)\) 只有 \(O(n\log n)\) 种。

考虑对 \(O(n^2\log n)\) 组 \(f(l,r,p)\) 进行随机二分，每一次可以扔掉期望一半，假设当前随机取的中点为 \(f(L,R,P)\)。我们考虑 DP，令 \(f_{i,j}\) 表示当前最后一段满足 \(p=i,r=j\)，最小的操作次数，那么限制就变成了判断 \(f_{n,n}\le k\) 即合法。

我们考虑从小到大枚举 \(p\)，将第一维滚动，然后在枚举 \(O(n\log a)\) 种 \(r\)，注意到 \((l,r,p)\) 的权值随着 \(l\) 递减而递增，所以存在一个分界点 \(lpos\)，满足 \(l\ge lpos\)，\(f(l,r,p) \le f(L,R,P)\)。那么，我们就可以树状数组维护后缀 \(dp_{j} -j\) 的 \(\max\)，单点 chkmax，维护 DP。

现在问题转化成如何求出 \(lpos\)。我们先在外层二分，那么现在我们只需要判断 \(f(l,r,p)\) 和 \(f(L,R,P)\) 的大小关系。我们考虑二分+哈希求出 LCP，考虑计算 \(\lfloor f(l,r,p)2^t\rfloor \pmod {10^9+7}\)。

我们令 \(h=p-t\)，这里是 \(0\) 次项的位置，然后分类讨论。

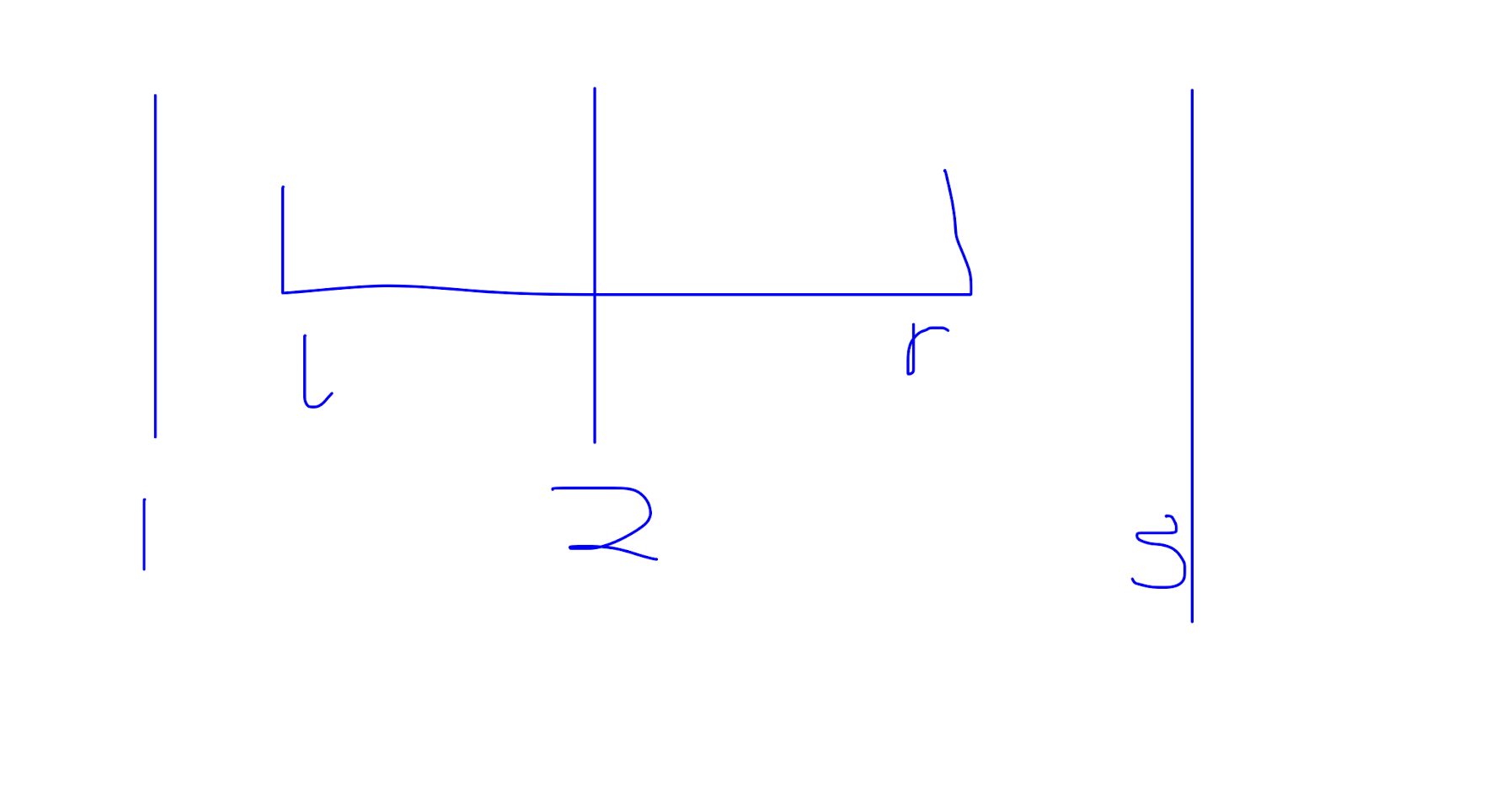
不难发现，我们只需要求出 \(a_i2^i\) 的前缀和，以及一个区间的进位即可。这里说的一个区间的进位是指，对于 \((l,r)\)，求出 \(\lfloor\sum_{i=l}^{r}\frac{a_i}{2^{r-i+1}}\rfloor\)。我们考虑对于 \(l\ge r-lim\)，预处理即可。对于 \(l<r-lim\)，我们发现由于这部分的贡献和 \(<1\)，所以最多只会使得下取整的值增加 \(1\)。注意到关于 \(l\) 减小是单调上升的，所以我们维护 \(pos_i\) 表示 \(l\le pos_i\) 下取整的值会再额外增加 \(1\) 即可。这里求出 \(pos_i\) 可以从左往右递推。

求出 LCP 之后考虑具体计算 \(2^{-t}\) 那一位的值，只需要 \(\lfloor f(l,r,p)2^t\rfloor-2\lfloor f(l,r,p)2^{t+1}\rfloor\pmod {10^9 +7}\) 即可。

这样，我们分析一下时间复杂度。

1. 随机二分；
2. \((r,p)\)；
3. 二分 \(lpos\)；
4. 二分 LCP。

总共 \(4\) 个 \(\log\)，时间复杂度 \(O(n\log^3 n\log a)\)。

CTS 的评测机很慢，赛时进行了一些卡常：

1. 二分 \(lpos\) 时，上下边界可以设成随机二分的上下边界，正确性显然。虽然这样不能改变时间复杂度，但是可以优化常数。具体来讲，这部分的开销变成了 \(\log n+(\log n-1)+(\log n-2)+\cdots +1\)，带了 \(\frac{1}{2}\) 的常数；
2. 二分 LCP 的时候，由于大概率 LCP 较小，所以可以使用倍增。具体来讲，先从 \(2^0,2^1,\cdots,2^t\)，再从 \(2^{t-1},2^{t-2},\cdots,2^0\)，实测本地随机数据能快超过一倍。