2024山西中考数学第15题

如图，在 $▱ABCD$ 中，$AC$ 为对角线，$AE⊥BC$ 于点 E，点 $F$ 是 $AE$ 延长线上一点，且 $∠ACF = ∠CAF$，线段 $AB$，$CF$ 的延长线交于点 $G$，若 $AB=\sqrt{5}$，$AC=4$，$\tan∠ABC=2$，则 $BG$ 的长为_________.

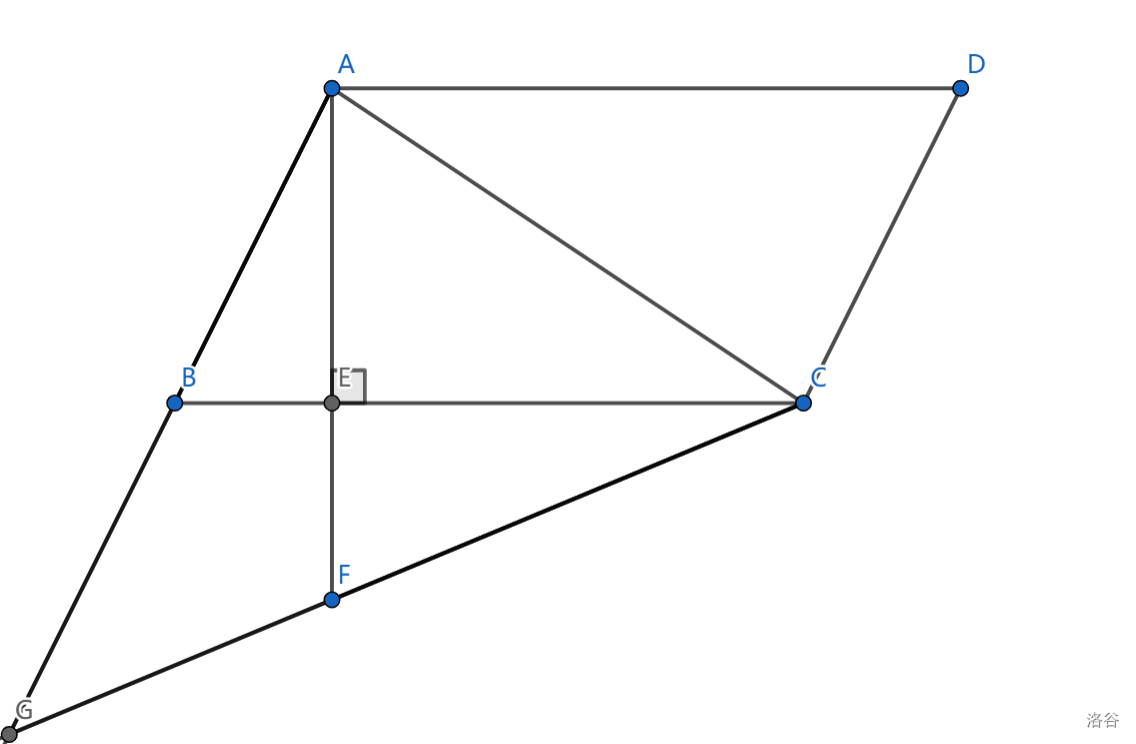
解析

勾股定理+建系

过程

解：由题得，$AE=2$，$BE=1$。

$∵BC=4,BE=1$

$∴CE=3$

在$Rt△CEF$中，$∠CEF=90$，

由勾股定理得，$CE^{2}+EF=CF^{2}$

设 $EF=x$，则 $CF=x+2$。

由题得 $x^{2}+3=(x+2)^{2}$

解得 $x=\frac{5}{4}$

$∴EF=3$

以点 $E$ 为原点，$BC$ 为 $x$ 轴，$AF$ 为 $y$ 轴，建立平面直角坐标系

由题得，$A(0,2),B(-1,0),C(3,0),F(0,-\frac{5}{4})$

设 $y=k_{1}x+b_{1}(k_{1}\neq0)$ 的图像经过点 $A(0,2),B(-1,0)$
由题得，
$
\begin{cases}
b_{1}=2\
-k_{1}+b_{1}=0
\end{cases}
$

解得
$
\begin{cases}
k_{1}=2\
b_{1}=2
\end{cases}
$

$∴y_{AB}=2x+2$

同理，$y_{CF}=\frac{5}{12}x-\frac{5}{4}$

联立两式得

$
\begin{cases}
y=2x+2\
y=\frac{5}{12}x-\frac{5}{4}
\end{cases}
$

解得
$
\begin{cases}
x=-\frac{39}{19}\
y=-\frac{40}{19}
\end{cases}
$

$∴G(-\frac{39}{19},-\frac{40}{19})$

又$∵B(-1,0)$

$∴BG=\sqrt{[-1-(-\frac{39}{19})]^{2+[0-(-\frac{40}{19})]}2}=\sqrt{(\frac{20}{19})^{2+(\frac{40}{19})}2}=\sqrt{\frac{2000}{361}}=\frac{20\sqrt{5}}{19}$

$∴BG=\frac{20\sqrt{5}}{19}$