【持续更新中】线段树全集

引入

一个数列，单点修改（加），区间查询（和）。

上述问题有很多种解法，如树状数组、分块、平衡树等，今天的主题是著名的线段树。

正题

（不确保按难度升序排序，自己看着目录调顺序吧）

线段树基本原理

因为需要区间查询，所以我们希望有一些捷径能将部分的数的和提前算好，并能够直接上手用，这样可以节省不少的时间。

这正是线段树、树状数组、分块的主要思想。

考虑将整个序列平均分成两截，将两部分的数提前算好，修改的时候顺手再改一下，就能省掉一部分时间。

但是这还是不够优秀。

接下来又有两条路可以走：

• 将序列拆分成的段数增加，用同样的方法维护（这就是分块的方向）。
• 将分成的两截继续分，分到每段只有一个数为止（这就是线段树和树状数组的思想），形成一个类似树的结构。

第一条的最优时间复杂度是 \(\sqrt{n}\) 级别的，但是第二条理论上是可以做到 \(\log n\) 级别的，所以我们试着走第二条路。

走第二条路得到的结构是一棵树，我们可以不用链式建树，用堆式建树即可（即父亲节点编号为 \(i\)，则两个儿子的编号为 \(2i\) 和 \(2i + 1\)）。

根据上文中提到的方法，我们需要将这个树形的数据结构（线段树）上的所有点都给予一个权值 \(sum\)，代表该结点管辖的所有结点之和。

因为每个结点上的 \(sum\) 都需要从各自儿子结点上传过来，所以需要有一个权值上传的函数。

void pushup(int id) {sum[id] = sum[ls] + sum[rs]; // ls,rs 代表两个儿子的编号，下同
}

每一次查询 \(\left[L, R\right]\)，找到所有被完全包含的加一下即可（但是一定要全取深度最浅的，这样不仅不会算重还能节省部分的时间）。

示例代码：

int query(int id, int lft, int rht, int l, int r) { // 从左到右依次是：目前找到的结点编号、结点管辖的左端点、右端点、查询的左端点、右端点if (lft > r || rht < l) return 0; // 如果不在结点的辖区内，返回 0 不考虑。if (l <= lft && rht <= r) return sum[id]; // 如果完全包含，不用往下递归，直接返回。int mid = (lft + rht) >> 1; // 因为分是对半分，所以取中点return query(ls, lft, mid, l, r) + query(rs, mid + 1, rht, l, r); // 递归返回
}

但是它若修改 \(x\)，阁下又该如何应对？

其实这也不难，从根（代表 \(\left[ 1, n \right]\) 的点）开始，往下找代表 \(\left[ x, x\right]\) 的点，并将沿途的所有点都加上修改的值即可。

示例代码：

void change(int id, int lft, int rht, int x, int v) { // 从左到右依次是：目前找到的结点编号、结点管辖的左端点、右端点、修改的下标、修改的权值if (x < lft || rht < x) return; // 如果不包含在区间中，就返回if (lft == rht) return sum[id] += v, void(); // 如果恰好找到了，就修改回去int mid = (lft + rht) >> 1;change(ls, lft, mid, x, v), change(rs, mid + 1, rht, x, v); // 递归修改pushup(id); // 记得上传
}

大家可以参考图 \(1\) 配合理解上述内容。

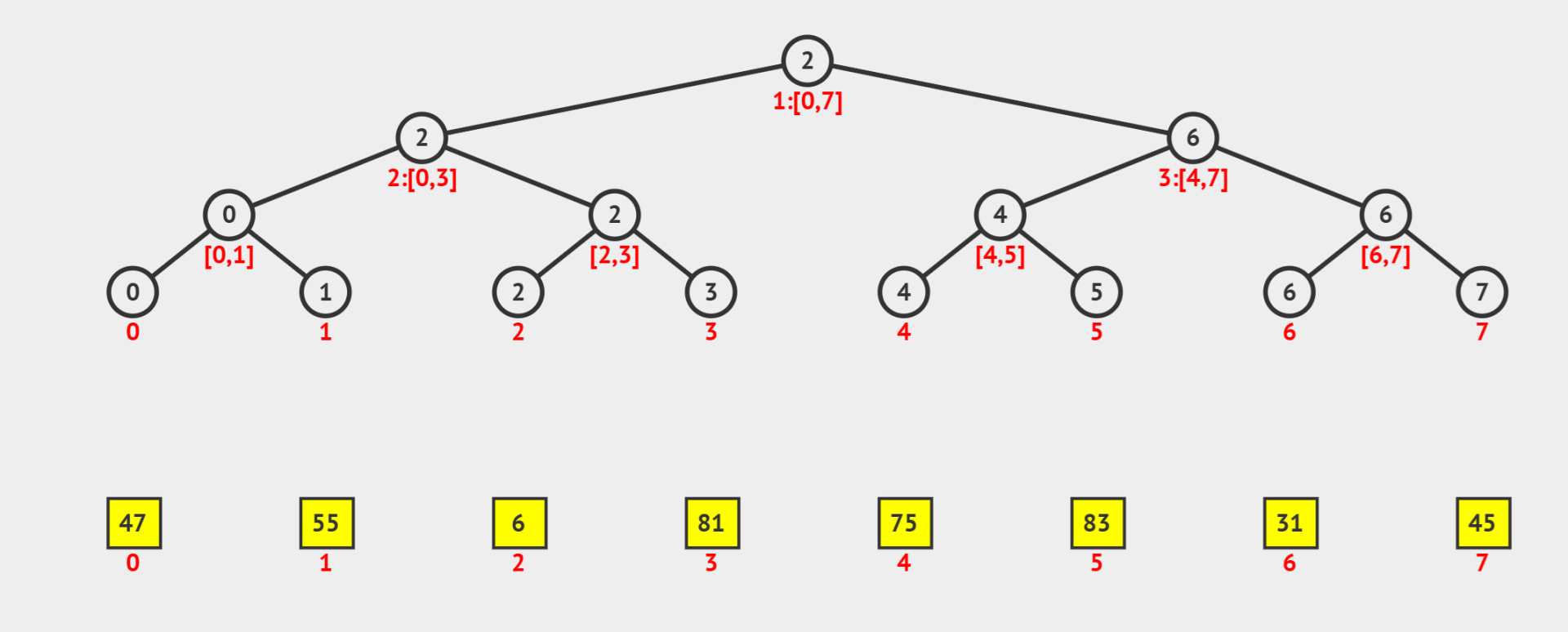
（图 \(1\)，来自 visualgo.net）

时空复杂度放到后面分析。

懒标记基本原理

那如果单修换成区修呢？

显然不可能一个一个地改，那该怎么办？

先放下线段树，我们举一个形象的例子。

---

你是一名学生，你的老师给你们班委派了一份作业。

并且老师嘱咐她会突击检查。

你想着等老师检查再做，就开始玩florr。

突然有一天，老师要突击检查，但是没检查到你，你放心了，还是不需要做。

但是这天，老师要检查你，你只好把所有的陈年旧账翻出来做了，交给老师。

老师没检查出问题，以为你是一个按时做作业的好学生。

---

故事讲完了，但是线段树还没完。

我们可以将区修类比成老师布置作业，检查看作查询。

而树上的每个点都看作你不做作业的学生。

那么对于每一个树上的结点，我们再加一个变量 \(tag\)，存储所有的在当前结点上做的区修值之和（因为多次区间加可以看作一次大的区间修改），先存在那，不慌下传，等查询到的时候再下传。

因为这是人类懒才制造出来的东西，所以叫“懒标记”。

示例代码：

void pushdown(int id) { // 将存储于结点 id 的懒标记下传if (tag[id]) { // 如果该结点上存有标记tag[ls] += tag[id], tag[rs] += tag[id]; // 将标记传递到两个子结点的标记sum[ls] += tag[id] * len[ls]; // 传递到两个儿子结点的 sum 信息中，但是修改是对区间中每个数的修改，所以要乘上区间长度sum[rs] += tag[id] * len[rs];tag[id] = 0; // 已经下传完，不用留着}
}
int query(int id, int lft, int rht, int l, int r) {if (lft > r || rht < l) return 0; if (l <= lft && rht <= r) return sum[id];pushdown(id); // 记得 pushdown，否则还没来得及做就被检查了int mid = (lft + rht) >> 1;return query(ls, lft, mid, l, r) + query(rs, mid + 1, rht, l, r);
}
void change(int id, int lft, int rht, int l, int r, int v) { if (lft > r || rht < l) return;if (lft == rht) return sum[id] += (rht - lft + 1) * v, tag[id] += v, void(); // 修改，记得加标记pushdown(id); // 记得 pushdownint mid = (lft + rht) >> 1;change(ls, lft, mid, l, r, v), change(rs, mid + 1, rht, l, r, v);pushup(id);
}

重生之扫描线 + 线段树

看一道题：

P5490 【模板】扫描线 & 矩形面积并

假设有一条直线，初始与 \(x\) 轴平行，不断往上扫，然后在线段树上更新。

像这样：

（图 \(2\)，图片来自 oi-wiki）

最后将扫过的长度乘上宽即可算出一条长方形的面积了。

代码不放了，当时写得很丑。

重生之怎么又是扫描线（广义）

上文解决了矩阵面积并问题，是具象的扫描线（当然也是狭义的）。

但是有一些序列问题也可以转化为扫描线。

P1908 逆序对

没错就是它，虽然并没有用线段树（也不是不行），但是它的树状数组解法运用了扫描线思想。

对于每一个数 \(p_i\)，将 \((i, p_i)\) 放到坐标轴上。

像这样：

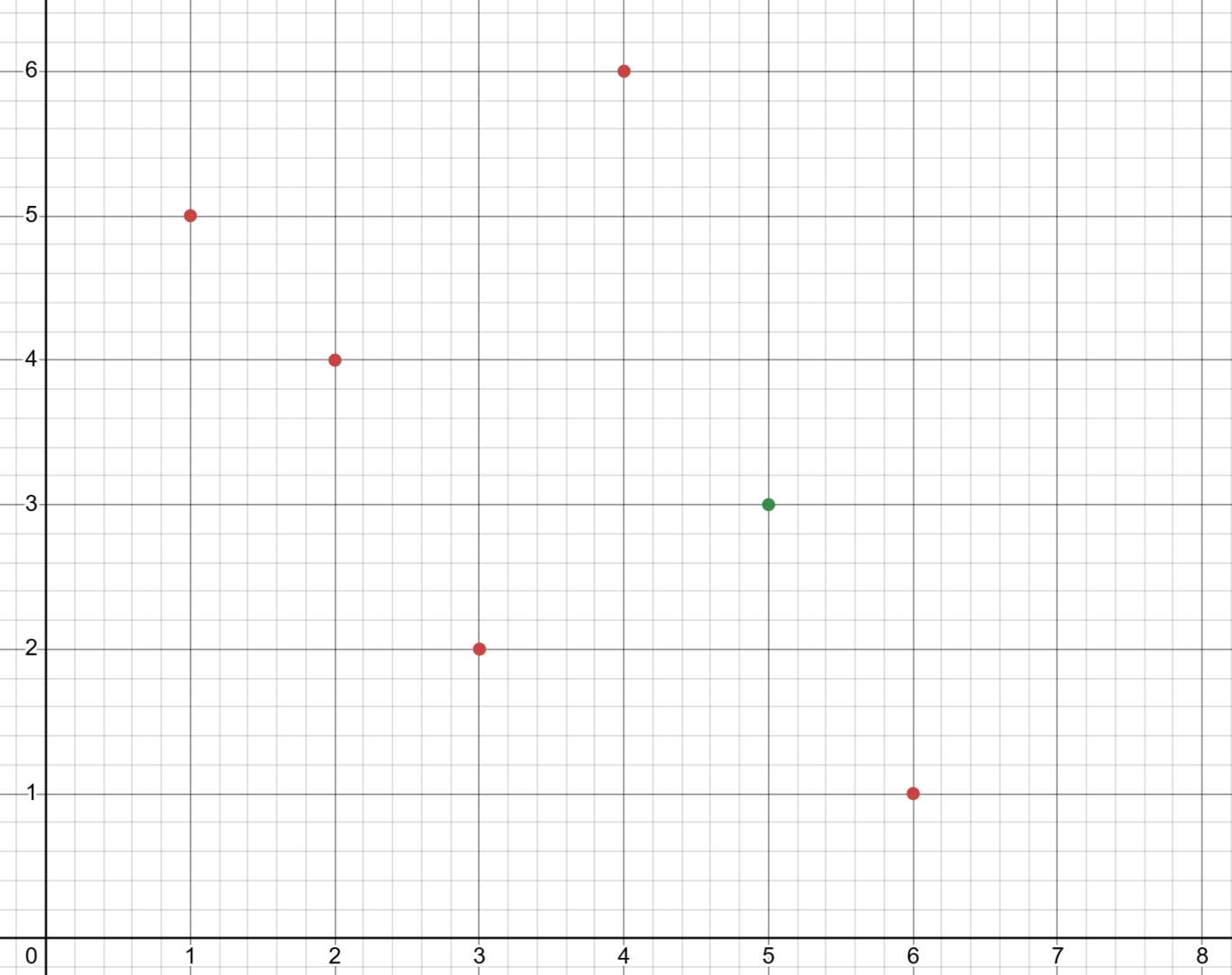
（图 \(3\)，自己的，以样例为例）

而逆序对的定义是 \(i > j, p_i < p_j\)，那么就相当于找所有在 \((i, p_i)\) 的左上方的点，像这样：

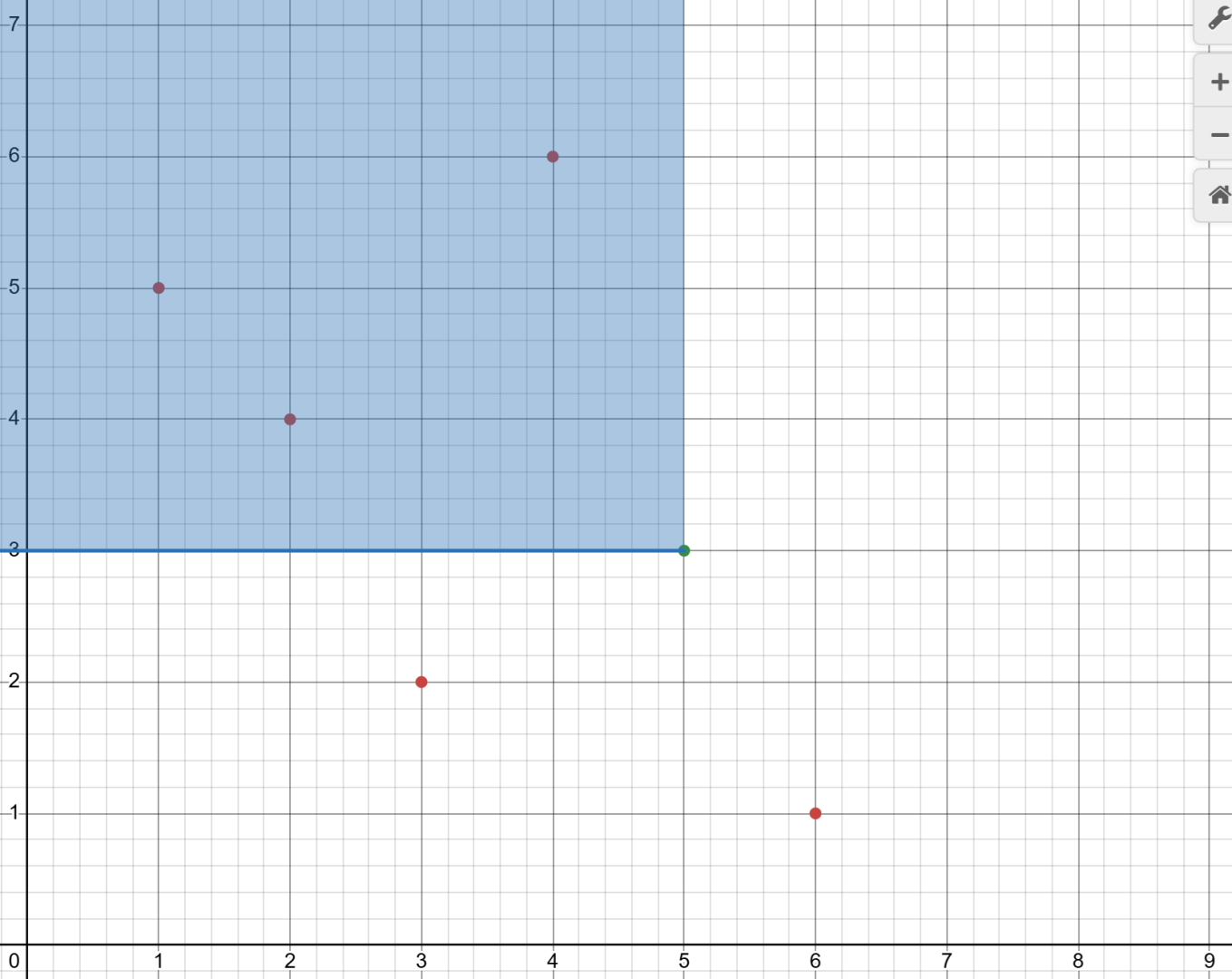
（图 \(4\)）

好，你已经知道广义扫描线是什么了，我们来小试牛刀一下。

Pudding Monsters

区区紫题，何足惧哉？

因为每行每列只会有一个 Monster，所以可以将二维压缩成一维，横坐标作为下标，纵坐标作为值记为 \(a\) 数组。

不要被紫题的表象吓到，冷静分析，它求的无非是满足以下条件的 \((L, R)\) 对数：

\[\max_{i = L}^Ra_i - \min_{i = L} ^ {R}a_i + 1 = len \]

可以来推柿子了：

\[\max_{i = L}^Ra_i - \min_{i = L} ^ {R}a_i + 1 = len \]

\[\max_{i = L}^Ra_i - \min_{i = L} ^ {R}a_i - len = -1\\ \]

仔细分析，发现：

\[\max_{i = L}^Ra_i - \min_{i = L} ^ {R}a_i - len \ge -1 \]

那不好办了，直接算算上述值的最小值个数不就行了。

但是复杂度好像还是 \(n^2\log n\) 的，肯定过不了……

不过，你可别忘了，这题要用扫描线。

枚举 \(R\)，利用单调队列更新 \(\max\)、\(\min\)，修改以后，查询最小值个数之和即可。

小小紫题，不过如此。

#include <bits/stdc++.h>
#define int long long
#define pii pair<int, int>
#define FRE(x) freopen(x ".in", "r", stdin), freopen(x ".out", "w", stdout)
#define ALL(x) x.begin(), x.end()
using namespace std;int _test_ = 1;const int N = 3e5 + 5;int n, a[N], b[N];struct node {int v, l, r; // 存储左右端点和权值
};bool operator<(node a, node b) { return a.v < b.v; }
bool operator>(node a, node b) { return a.v > b.v; }
bool operator<(node a, int b) { return a.v < b; }
bool operator>(node a, int b) { return a.v > b; }
bool operator<(int a, node b) { return a < b.v; }
bool operator>(int a, node b) { return a > b.v; }struct segment {#define ls (id << 1)#define rs (id << 1 | 1)int mn[N << 2], cnt[N << 2], tag[N << 2]; // 最小值、最小值个数、加和懒标记void pushup(int id) {mn[id] = min(mn[ls], mn[rs]);if (mn[ls] < mn[rs]) cnt[id] = cnt[ls];if (mn[ls] > mn[rs]) cnt[id] = cnt[rs];if (mn[ls] == mn[rs]) cnt[id] = cnt[ls] + cnt[rs]; }void pushdown(int id) {if (tag[id]) {mn[ls] += tag[id], mn[rs] += tag[id];tag[ls] += tag[id], tag[rs] += tag[id];tag[id] = 0;}}void build(int id, int lft, int rht) {if (lft == rht) return mn[id] = b[lft], cnt[id] = 1, void();int mid = (lft + rht) >> 1;build(ls, lft, mid), build(rs, mid + 1, rht);pushup(id);}void change(int id, int lft, int rht, int l, int r, int v) {if (lft > r || rht < l) return;if (l <= lft && rht <= r) {mn[id] += v;tag[id] += v;return;}pushdown(id);int mid = (lft + rht) >> 1;change(ls, lft, mid, l, r, v), change(rs, mid + 1, rht, l, r, v);pushup(id);}pii query(int id, int lft, int rht, int l, int r) {if (lft > r || rht < l) return {LLONG_MAX, 0};if (l <= lft && rht <= r) return {mn[id], cnt[id]};int mid = (lft + rht) >> 1;pii x = query(ls, lft, mid, l, r), y = query(rs, mid + 1, rht, l, r);if (x.first < y.first) return x;if (x.first > y.first) return y;return {x.first, x.second + y.second};}
} seg;void init() {}void clear() {}void solve() {cin >> n;for (int i = 1, l; i <= n; i++) cin >> l >> a[l];for (int i = 1; i <= n; i++) b[i] = i; // 这里用了一个比较巧妙的方法，放后面说一下seg.build(1, 1, n);stack<node> mx, mn; // 两个单调栈int ans = 0;for (int i = 1; i <= n; i++) {int lft = i;while (mx.size() && a[i] > mx.top()) {lft = mx.top().l;seg.change(1, 1, n, mx.top().l, mx.top().r, -mx.top().v); // 将所有不再是最大值的合并到一起mx.pop();}seg.change(1, 1, n, lft, i, a[i]); // 同意赋值，上文中 max 部分是正的所以是 + a[i]mx.push({a[i], lft, i});lft = i;while (mn.size() && a[i] < mn.top()) {lft = mn.top().l;seg.change(1, 1, n, mn.top().l, mn.top().r, mn.top().v); // 将所有不再是最小值的合并到一起mn.pop();}seg.change(1, 1, n, lft, i, -a[i]); // 同理，为 - a[i]mn.push({a[i], lft, i});ans += seg.cnt[1]; // 加上所有的总和}cout << ans;
}signed main() {ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);
//	cin >> _test_;init();while (_test_--) {clear();solve();}return 0;
}

代码中的 for (int i = 1; i <= n; i++) b[i] = i; 不知道你注意到没有。

因为柿子中的 \(-len\) 不断在变，比较麻烦，将它统一加上 \(R + 1\)，此时 \(-len\) 就变成了 \(L\)，恰好就是 \(i\)，问题就迎刃而解了。

线段树维护最大子段和及相关问题

引入

link。

我们可以分析出上题就是带修改的最大子段和。

遇到这种类型的题目应该想到用线段树。

实现

对于原数列，先建起一棵线段树，每个节点包含 最大前缀、最大后缀、最大字段和、区间和 信息。

当你明确一道题是线段树时，要先思考 pushup 和 pushdown 怎么写，因为剩下的都是差不多的。 —— jzp.

因为本题是单查，没有 pushdown，就先考虑 pushup 怎么写：

• 最大前缀只可能是左儿子的最大前缀或是左儿子的和加上右儿子的最大前缀，即 \(maxl_i = \max\{maxl_l, sum_l + maxl_r\}\)。
• 最大后缀同理，\(maxr_i = \max\{maxr_r, sum_r, maxr_l\}\)。
• 最大子段和就是左儿子最大子段和或右儿子最大子段和或左儿子最大后缀加右儿子最大前缀，即 \(maxs_i = \max\{maxs_l, maxs_r, maxr_l + maxl_r\}\)。
• 区间和很简单，不赘述。

void pushup(int id) {sum(id) = sum(ls) + sum(rs);maxl(id) = max(maxl(ls), sum(ls) + maxl(rs));maxr(id) = max(maxr(rs), sum(rs) + maxr(ls));maxs(id) = max(max(maxs(ls), maxs(rs)), maxr(ls) + maxl(rs));
}

那么对于每一次询问，我们找到线段树上的左右端点 \(l\)、\(r\) 对应的两点 \(p_l\)、\(p_r\)。

当我们从上往下爬树爬到 \(k = LCA(p_l, p_r)\) 时，\(l\) 和 \(r\) 就会分开为两个区间。

此时答案有几种可能：

• \(l \le r \le m\)，其中 \(m\) 为该区间的中间点，此时递归左侧得到答案。
• \(m \lt l \le r\)，此时递归右侧得到答案。
• \(l \le m \lt r\)，此时合并两次得到的答案。

以上三者取最大值返回。

这跟 cdq 分治的思想有异曲同工之妙。

当 \(l\) 与 \(r\) 并没有分叉时，就直接走下去即可。

那么此时查询也可以顺利地写出来了。

segment query(int id, int lft, int rht, int l, int r) {	// 这里用 segment 作为返回值是因为每层递归都需要用到下一层递归的结果if (l <= lft && rht <= r) return seg[id];int mid = (lft + rht) >> 1;if (r <= mid) return query(ls, lft, mid, l, r);if (l > mid) return  query(rs, mid + 1, rht, l, r);segment a = query(ls, lft, mid, l, r), b = query(rs, mid + 1, rht, l, r), t;t.sum = a.sum + b.sum;t.maxl = max(a.maxl, a.sum + b.maxl);t.maxr = max(b.maxr, b.sum + a.maxr);t.maxs = max(max(a.maxs, b.maxs), a.maxr + b.maxl);return t;
}

整体代码：

struct segment_tree {#define ls (id << 1)#define rs (id << 1 | 1)#define sum(id) seg[id].sum#define maxl(id) seg[id].maxl#define maxr(id) seg[id].maxr#define maxs(id) seg[id].maxsstruct segment {int maxl, maxr;int sum, maxs;} seg[N << 2];void pushup(int id) {sum(id) = sum(ls) + sum(rs);maxl(id) = max(maxl(ls), sum(ls) + maxl(rs));maxr(id) = max(maxr(rs), sum(rs) + maxr(ls));maxs(id) = max(max(maxs(ls), maxs(rs)), maxr(ls) + maxl(rs));}void build(int id, int lft, int rht) {if (lft == rht) {sum(id) = a[lft];maxl(id) = maxr(id) = maxs(id) = a[lft];return;}int mid = (lft + rht) >> 1;build(ls, lft, mid), build(rs, mid + 1, rht);pushup(id);}void change(int id, int lft, int rht, int x, int v) {
//		if (lft > x || rht < x) return;if (lft == rht) {
//			a[lft] = v;sum(id) = v;maxl(id) = maxr(id) = maxs(id) = v;return;}int mid = (lft + rht) >> 1;if (x <= mid) change(ls, lft, mid, x, v); else change(rs, mid + 1, rht, x, v);pushup(id);}segment query(int id, int lft, int rht, int l, int r) {
//		if (lft > r || rht < l) return ;if (l <= lft && rht <= r) return seg[id];int mid = (lft + rht) >> 1;if (r <= mid) return query(ls, lft, mid, l, r);if (l > mid) return  query(rs, mid + 1, rht, l, r);segment a = query(ls, lft, mid, l, r), b = query(rs, mid + 1, rht, l, r), t;t.sum = a.sum + b.sum;t.maxl = max(a.maxl, a.sum + b.maxl);t.maxr = max(b.maxr, b.sum + a.maxr);t.maxs = max(max(a.maxs, b.maxs), a.maxr + b.maxl);return t;}
} seg;

我们可以通过线段树维护最大子段和来推广到其他类似的问题。

（复制了一下之前写的）