【持续更新】【专题】初等数论
Designed By:FrankWkd 【100%原创】【禁止搬运】
Updated at 2025.01.26
前言:
- 主要从线性筛开始速通初等数论
- 尽可能的多证明结论而不是阐述结论。如果你只是想回顾结论,请看其他人的 \(Blog\) .
一、基础概念
- 整除:对于两个正整数 \(a,b\), 存在一个数 \(k\) ,使得 \(a=bk\),则称 \(b\) 整除 \(a\).记作 \(b\ |\ a\).
- 带余除法:对于两个正整数 \(a,b\), 存在两个数 \(k,r\) ,使得 \(a=bk+r\),则称 \(b\) 除 \(a\) 商 \(k\) 余 \(r\).(\(b\div a=k\dots r\))
- 因数:能整除一个数的数被称为这个数的因数.
- 公因数:两个数共同具有的因数被称为这两个数的公因数。
- 质数:只有 \(1\) 喝和它本身的数被称为质数。\(2\) 是质数。
- 质因子:一个数的质因数(既是它的因数也是质数的数)被称为质因子。
- 算术基本定理:一个数能表示成其若干个质因数的乘积(类似于分解质因数的逆运算)。
二、基础算法
- 因数分解:分解出正整数 \(x\) 的所有因子。
- 复杂度:\(O(\sqrt n)\)
- 埃氏筛:快速筛出 \(1-n\) 中所有的素数。
- 复杂度:\(O(nloglogn)\)
- 质因数分解:快速分解出 \(n\) 的所有质因子。
- 复杂度:\(O(\sqrt{n})\)
- 欧几里得算法:快速求出两个数 \(a,b\) 的最小公约数( \(gcd\) ).
- 核心公式:\(gcd(a,b)=gcd(b,a\ mod\ b)\).
三、Euler欧拉筛(线性筛)
关于线性筛
- 一种基于埃氏筛的高效筛法。
- 时间复杂度 \(O(n)\)。
- 保证每一个素数只被其最小质因子筛除。
- 每个素数只是被筛除一次。
让我们一个一个地证明这些结论:
证明
注:请结合代码理解。
void getprime() {for (int i = 2; i <= n; i++) {if (!vis[i]) p[++k] = i;//k为素数个数for (int j = 1; j <= k and i * p[j] <= n; j++) {vis[i * p[j]] = 1;if (i % p[j] == 0) break;}}
}
-
- 为什么这样写呢?怎么保证每个合数都被无遗漏地筛除呢?
- 设一合数为 \(x\) ,因为它是合数,所以它一定能表示为 \(x=pi\) 的形式(一个合数可以分解成两个数的乘积)。
- 我们令 \(p\) 为 \(x\) 的最小质因子。
- 现在请看代码,可知:当 \(i\ mod\ p=0\) 时循环立即中断。通俗的理解就是:当 \(i\) 是 \(p\) 的倍数时,循环直接 \(break\).
- 那么,让我们回归到程序,第二层循环遍历的是所有已经筛出来的质数,由程序可得:只要有一个数符合循环 \(break\) 的标准,循环就中断了。
- 符合循环 \(break\) 标准的质数肯定是一个小于 \(p\) 且是 \(i\) 因数的质数,对吧?
- 既然这个数是 \(i\) ,的质因子,\(i\) 又是 \(x\) 的因子,这个数就是 \(x\) 的质因子。
- 因为 \(p\) 是 \(x\) 的最小质因子,没有比它更小的质因子了,所以第二层循环中不可能再出现比 \(p\) 小而且是 \(x\) 的质因子的数了。
- 所以 \(x\) 一定能被筛到。
- 得证(反证法,不是特别严谨,有问题或疑问请评论或私信)。
-
- 那又如何保证每一个数只被其最小质因子筛一次呢?
- 我们设将要被筛除的合数为 \(x\) ,将其分解为 \(x=py=qz\) 的形式。
- 其中,\(p\) 是 \(x\) 的最小质因子,\(q\) 是 \(x\) 的另一个质因子(比 \(p\) 大)
- 接下来让我们再次分解: \(x=pqk\),\(p,q\) 就是上面的 \(p,q\) ,\(k\) 为使得上面式子成立的数.
- 那么现在有:
\[x=p(qk) \]\[x=q(pk) \]- 我们设 \(y=qk\), \(z=pk\), 我们不难得到:\(z\) 中一定含有质因子 \(p\) 。而且 \(p<q\) 。
- 当 \(i\) 枚举到 \(z\) 、\(j\) 枚举到 \(p\) 时,\(i\ mod\ j=0\) 会先一步成立,所以 \(j\) 不会再往下面枚举到 \(q\) ,从而避免了枚举到 \(py=x\) 之后又枚举到 \(qz=x\) ,造成重复计算.而且每个合数仅仅被其最小质因子(也就是 \(p\))筛除.
- 让我们举个栗子:
-
- 要筛除的合数 \(x\) 是 \(35\)
-
- 最小质因子 \(p\) 是 \(5\)
-
- 质因子 \(q\) 是 \(7\)
-
- \(35\) 可以写成 \(35=5*7=7*5(x=py=qz)\) 的形式。
-
- \(35\) 还可以写成 \(35=5*7*1(x=pqk)\) 的形式。
-
- 由第五步中的式子转化为:\(35=5*(7*1)=7*(5*1)(x=py=qz)\) 的形式。
-
- 由第四步可知:\(y=7,z=5\).
-
- 由第六步可知:\(y=7*1,z=5*1\).
-
- 那么,\(z\) 中含有 \(p\) 的时候就会 \(break\),刚好是在筛出 \(35\) 这个合数之后,以保证不会再往下筛,从而避免一个数被筛多次的情况。
-
-
- 为什么复杂度是线性( \(O(n)\) )的?
- 因为每个质数只会被记录一次,每个合数只是会被筛除一次,但是埃氏筛会将每个合数筛 \(loglogn\) 次( \(O(nloglogn)\) ),这就是欧拉筛(线性筛)为什么复杂度是 \(O(n)\) 的原因。
例题:
-
- 题面描述:\(T\) 组数据。每次给定一个整数 \(n\),求 \(n\) 所有质因子的按位异或和.
- 数据范围:\(1\le T\le 10^5,2\le N\le 10^8\)
- 思路:如果每次把 n 都除以自己的最小质因子,那么可以 \(O(log n)\) 完成一次质因子分解。
如何求出最小质因子?
在线性筛的时候,每个数都被自己的最小质因子筛掉。所以我们只要在当一个数被筛的时候记录筛掉它的数即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e8 + 5;
bitset <N> vis;
int mn[N];
int p[N / 10];
void getprime() {for (int i = 2; i <= n; i++) {if (!vis[i])p[++k] = i, mn[i] = i;for (int j = 1; j <= k && i * p[j] <= n; j++) {vis[i * p[j]] = 1;mn[i * p[j]] = p[j];if (i % p[j] == 0)break;}}
}
int main() {int T, n;cin >> T;while (T--) {cin >> n;int ans = 0;while (n > 0) ans ^= nm[n], n /= nm[n];cout << ans << '\n';}
}
四、欧几里得定理及其扩展&裴蜀定理
欧几里得定理(\(gcd\))
定理
- 先放定理:设 \(a,b\) 是两个整数,且 \(b \neq 0\),则 \(gcd(a,b)=gcd(b,a\ mod\ b)\)。
- 时间复杂度:\(O(log\ min(a,b))\)
前置知识
- 模运算( \(\%\) ): 相信你学习到这里已经掌握了几乎所有模运算性质,这里我们只需使用到一个,即:
-
\[a\ mod\ b=a-\left \lfloor \frac{a}{b} \right \rfloor \times b \]
-
\[a=a\ mod\ b+\left \lfloor \frac{a}{b} \right \rfloor \times b \]
- 为什么是这样呢?
- 这里的 \(\left \lfloor \frac{a}{b} \right \rfloor\) 就是 \(a\div b\) 所得的整数商。将 \(a\) 减去这个值所得的就是 \(a\div b\) 所得的余数。也就是 \(a\ mod\ b\) 。
- 我们举例说明:
-
\[10\%3=10-\left \lfloor \frac{10}{3} \right \rfloor \times 3 \]
-
\[10=10\%3(余数部分)+\left \lfloor \frac{10}{3} \right \rfloor \times 3(整数商) \]
-
-
证明
下面开始证明(汗流浃背
- 设 \(d=gcd(a,b)\) ,则 \(d\) 能整除 \(a,b\), 即:
-
\[d|a\ \ d|b \]
-
- 可以写成:
-
\[a=k_1d,b=k_2d\ (k_1,k_2\in \mathbb {Z(整数)}) \]
-
- 根据前置知识,\(a\%b\) 可以写成:
-
\[a\%b=a-\left \lfloor \frac{a}{b} \right \rfloor \times b \]
-
- 将 \(a=k_1d,b=k_2d\) 带入得:
-
\[a\%b=k_1d-\left \lfloor \frac{k_1d}{k_2d} \right \rfloor \times k_2d \]
-
- 根据分数线的性质消元得:
-
\[a\%b=k_1d-\left \lfloor \frac{k_1}{k_2} \right \rfloor \times k_2d \]
-
- 设 \(q=\left \lfloor \frac{k_1}{k_2} \right \rfloor\) ,并将其带入得:
-
\[a\%b=k_1d-qk_2d \]
-
- 提出公因数 \(d\) 可得:
-
\[a\%b=(k_1-qk_2)d \]
-
- 因为 \(k_1,k_2\) 被定义为整数,且 \(q\) 已经经过了向下取整,所以 \(q\) 也是整数,故 \(k_1+qk_2\) 也是整数。
- 立得: \(d\) 整除 \(a\ mod\ b\) .
- 所以 \(d\) 既是 \(a,b\) 的最大公约数,也是 \(b,a\ mod\ b\) 的公约数。
- 反过来,设 \(d'=gcd(b,a\ mod\ b)\), 则 \(d'\) 整除 \(b,a\ mod\ b\) .
- 由前置知识得: \(a=a\ mod\ b+\left \lfloor \frac{a}{b} \right \rfloor \times b\)
- 因为: \(d'\) 整除 \(a\ mod\ b,b\),
- 所以: \(d'\) 整除 \(a\ mod\ b,\left \lfloor \frac{a}{b} \right \rfloor \times b\),
- 所以 \(d'|a\). (\(d'\) 整除 \(a\)).
- 所以:\(d'\) 整除 \(a,b\) .
- 整合
- 因为 \(d\) 是 \(a,b\) 的最大公因数,而 \(d'\) 只是 \(a,b\) 的公因数,不难得到:\(d'\le d\);
- 因为 \(d'\) 是 \(b,a\ mod\ b\) 的最大公因数,而 \(d\) 只是 \(b,a\ mod\ b\) 的公因数,不难得到:\(d\le d'\);
- 综上所述:
-
\[\left\{\begin{matrix}d\le d'\\d'\le d\end{matrix}\right. \]
- 该方程的解为:\(d=d'\)
-
- 即:
-
\[gcd(a,b)=gcd(b,a\ mod\ b) \]
- 当 \(b=0\) 时,\(gcd(a,b)=a\) ,因为 \(b\) 除以任何数都是 \(0\) ,那这个时候的最大公约数就理所应当的成为了 \(a\), 满足:\(a|a,b(0)|a\)。
-
- 我们只需要逐渐递归求解 \(gcd\) 即可,递归的终止条件为 \(b=0\) ,那时只需 \(return\ a\) 即可。
裴蜀定理
定理
先放定理:设 \(a,b\) 是不全为零的整数,则存在整数 \(x,y\),使得 \(ax + by=gcd(a,b)\)。
证明
请确保您已经理解 \(gcd\) 及其前置知识&证明。
- 当 \(b=0\) 时,由上面的证明可得:
-
\[gcd(a,b)=a \]
-
- 这时,\(x=1,y=0\) 显然满足 \(ax + by=gcd(a,b)\)。
- 我们假设对于 \(b,a\ mod\ b\),裴蜀定理成立,即存在整数 \(x_1,y_1\),满足
-
\[bx_1+(a\ mod\ b)y_1=gcd(b,a\ mod\ b) \]
-
- 由模运算的性质( \(gcd\) 的前置知识)可得:
-
\[a\ mod\ b=a-\left \lfloor \frac{a}{b} \right \rfloor b \]
-
- 将其带入得:
-
\[bx_1+(a-\left \lfloor \frac{a}{b} \right \rfloor b)y_1=gcd(b,a\ mod\ b) \]
-
- 拆括号得:
-
\[bx_1+ay_1-\left \lfloor \frac{a}{b} \right \rfloor by_1=gcd(b,a\ mod\ b) \]
-
- 移项得:
-
\[ay_1+bx_1-\left \lfloor \frac{a}{b} \right \rfloor by_1=gcd(b,a\ mod\ b) \]
-
- 合并同类项可得:
-
\[ay_1+(x_1-\left \lfloor \frac{a}{b} \right \rfloor y_1)b=gcd(b,a\ mod\ b) \]
-
- 由 \(gcd\) 的证明可得: \(gcd(a,b)=gcd(b,a\ mod\ b)\).
- 带入得:
-
\[ay_1+(x_1-\left \lfloor \frac{a}{b} \right \rfloor y_1)b=gcd(a,b) \]
-
- 令:
-
\[x=y_1,y=x_1-\left \lfloor \frac{a}{b} \right \rfloor y_1 \]
-
- 就找到了满足条件的 \(x,y\) 。
- 由数学归纳法可知,裴蜀定理对于任意不全为零的整数 \(a,b\) 都成立。
- 证毕。
扩展欧几里得算法(\(exgcd\))
提示:扩展欧几里得算法是一种使用程序求解问题的算法,不是定理!
目标
目标:由 \(gcd\) 和裴蜀定理求 \(ax+by=gcd(a,b)\) 的一组整数解。
做法
- 请确保您已经理解裴蜀定理的证明!
- 现在有方程 \(ax+by=gcd(a,b)\) ,求该方程的一组解。
- 由裴蜀定理可知,当 \(b=0\) 时,该方程的解为 \(x=1,y=0\)
- 根据裴蜀定理的结论可知:
-
\[x = y_1,y = x_1 - \lfloor\frac{a}{b}\rfloor y_1 \]
-
- 这样就得到了满足 \(ax + by = gcd(a, b)\) 的整数 \(x\) 和 \(y\)。
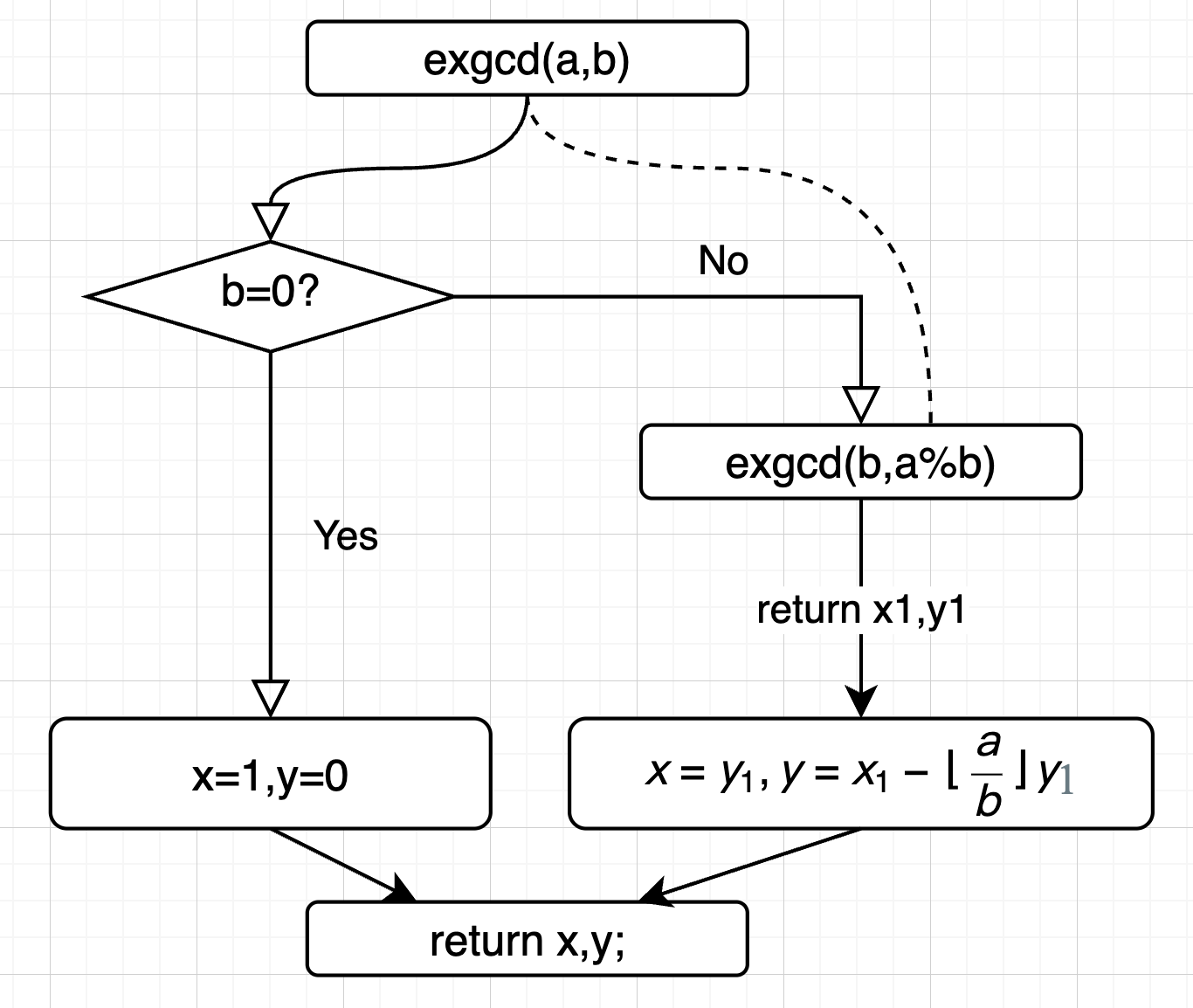
- 由裴蜀定理可知,\(x_1,y_1\) 是 \(bx_1+(a\ mod\ b)y_1=gcd(b,a\ mod, b)\) 的解。只要再次递归求解该方程即可。
- 详情见程序流程图:(绘图工具:draw.io)
五、同余
- 符号为 \(【\equiv】\).
- 定义:\(a\equiv b(mod\ p)\) 表示: \((a-b)\ mod\ p=0\),即 \(a-b=km\)(\(k\) 为整数)。
- 举个栗子:\(a=13,b=3,p=5\),计算 \((13-3)\ mod\ 5\) 正好是 \(0\),所以 \(5\) 能够整除 \(10\).我们这时称: \(13\equiv 3(mod\ 5)\)
- 性质: 若 \(a=b\):\(a\equiv b(mod\ m)\)
- 证明:
- 等式两边同时 \(mod\ p\) 得:
-
\[a\ mod\ x=b\ mod\ x \]
-
- 设 \(a=k_1x+r,b=k_2x+r\), 其中 \(k_1\) 是整数, \(r\) 就是 \(a\) 除以 \(x\) 后的余数,也就是 \(a\ mod\ x = r\)。
- 因为已知 \(a\% x = b\% x\),所以它们除以 \(x\) 后的余数相同,都为 \(r\),其中 \(k_2\) 是整数。
- 那么:
-
\[a-b=(k_1x+r)-(k_2x+r)=(k_1-k_2)x \]
-
- 因为 \(k_1,k_2\) 都是整数,所以说:\(a-b\) 是能被 \(m\) 整除的。
- 所以:
-
\[(a-b)\ mod\ x=0 \]
-
- 根据同余的定义得:
-
\[a\equiv b(mod\ x) \]
-
- 所以得出结论:等式两边同时模上一个数,等式依然成立。
六、逆元
前置知识
请保证你已经足够熟悉同余相关知识!
定义
- 先放定义: 给定正整数 \(a,m\),若存在整数 \(x\) 使得 \(a\times x\equiv 1(mod\ m)\),则称:\(x\) 是 \(a\) 在模 \(m\) 意义下的逆元,记作:\(a^{-1}\) .(注意这个写法是在模运算的情境下的一种表示,不是常规的倒数那种意思哦)
证明:
存在性:若 \(gcd(x,p)=1\) ,则 \(x\) 在模 \(p\) 意义下存在逆元。
- 根据裴蜀定理,若 \(gcd(x,p)=1\) ,则存在整数 \(s,t\) ,使得 \(xs+pt=1\)
- 现在我们考虑其在模 \(p\) 的意义下, \(1\ mod\ p=1\),根据同余的性质,\((xs+pt)\bmod p=1\bmod p\)
- 因为 \(pt\equiv 0(mod\ p)\),所以 \(pt\) 对 \((sx+pt)\bmod p\) 并没有贡献,可以省略。
- 那么舍去 \(pt\) 后的式子为:\(sx\bmod p=1\bmod p\)。
- 此时,\(s\) 就是 \(x\) 在模 \(p\) 意义下的逆元,即:\(x\ ·\ s\equiv1\pmod p\) .
- 得证:若 \(gcd(x,p)=1\) ,\(x\) 在模 \(p\) 意义下存在逆元。
必要性:若 \(x\) 在模 \(p\) 意义下存在逆元,则 \(gcd(x,p)=1\)。
- 当 \(x\) 在模 \(p\) 意义下存在逆元时,我们把这个逆元记作 \(y\),那么存在:
-
\[xy\equiv 1\pmod p \]
-
- 根据模运算的定义的逆运算得:
-
\[(xy-1)\bmod p=0 \]
-
- 我们将模运算写成这样的形式(\(k\) 为整数):
-
\[xy-1=kp \]
-
- 移项得:
-
\[xy-kp=1 \]
-
- 我们设 \(d=gcd(x,p)\),根据最大公约数的性质,\(d\) 整除 \(x,p\),即:
-
\[d\ |\ x,\ \ d\ |\ p \]
-
- 因为 \(d\) 整除 \(x\),所以 \(d\) 整除 \(xy\);
- 因为 \(d\) 整除 \(p\),所以 \(d\) 整除 \(kp\);
- 所以 \(d\) 整除 \(xy-kp\)
- 因为 \(xy-kp=1\) ,所以 \(d\) 整除 \(1\),又因为 \(d\) 是正整数,所以 \(d=1\),即:\(gcd(x,p)=1\)
- 综上,充分性和必要性均得证,所以 \(x\) 在模 \(p\) 同余下存在逆元当且仅当 \(gcd(x,p)=1\)。






![[Jest] 测试快照](https://resource.duyiedu.com/xiejie/2023-05-11-013235.png)
![[React Jest] 测试 Hook](https://resource.duyiedu.com/xiejie/2023-05-10-060112.jpg)