二分答案——时隔三个月的再次

暂且不提三个月未更新的主要原因（懒）

来自25年牛牛寒假营的一道寄巧题

part1

仔细考虑，显然满足单调性：假设时间T恰好发生第k次碰撞，那么T之前都不能发生，T之后只会越来越多

据此，又回到了上一篇的二分答案模板，但这里仍需考虑几个问题，如何简化问题？

对于高中物理，无需多言，对于质量相同的两个小球，只需要看作两个小球互相穿过即可，这样加上时间T，每个小球的始末状态都会确定，那么问题瞬间就清晰了许多，现在只需

要考虑两个小球是否发生碰撞。

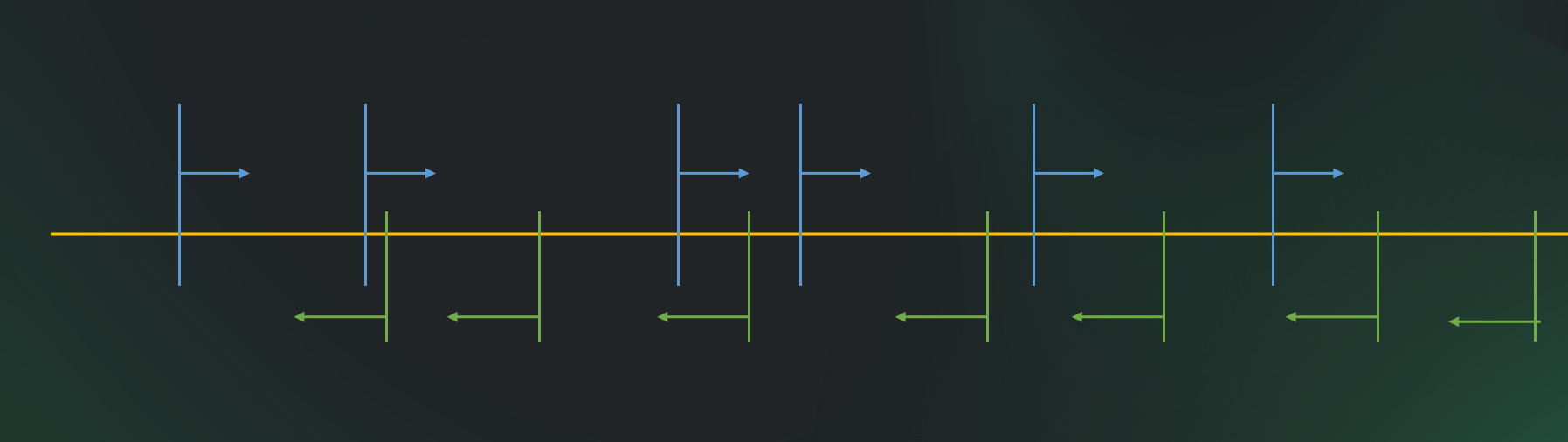
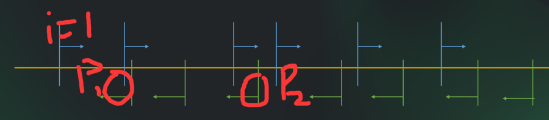
//雨巨的ppt偷的图

part2

对于类似上述情况，从第一个球开始考虑，（根据相对运动）只需判断其经过时间2T（速度都为1）与下方第一个球的距离差是否小于X，如果小于则发生碰撞，类似，直到蓝色第

一个球与当前最后一个黄色能发生碰撞，从此开始考虑第二个球，显然，第二个球一定能与上一个蓝色球发生碰撞的黄色球前面的都发生碰撞（前提当前蓝色前面没有黄色小球）

由此，对于外层循环，内层循环一定不会后退到某个位置（且内层循环的遍历与外层有关），可以使用双指针进行求解.

part3

现在假设上面p1表示第一个在i右边的小球，p2表示能与当前小球碰撞的最后一个小球，对于每个p1,其要碰撞满足的条件一定是在i右边（当前小球为i），对于p2，则一直到最后

一个能与当前球碰撞的小球，v[p2] <= i + T；则最后碰撞次数res += p2-p1;

part4(细节问题)

由于上述问题仅考虑整形范围内，实际有可能两个球距离相聚为1,仅用0.5s，且此题要求精度，上述的时间T实际是*2之后的时间，所以在处理最后的结果时需要注意细节问题

    #include<bits/stdc++.h>
#define N 1005
#define mod 998244353
#define int long long
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f3f;
ll check(ll t,vector<ll> &q,vector<ll> &p)
{ll res = 0;ll p1 = 0,p2 = 0;for(auto &i : q){while(p1 < p.size() && p[p1] < i)   p1++;//p1记录i右边的第一个小球while(p2 < p.size() && p[p2] <= i + t)  p2++;//p2记录能与当前小球碰撞的最后一个小球res += p2-p1;}return res;
}
void solve()
{vector<ll> q1,q2;ll n,k;cin>>n>>k;//int ans = 0;for(int i = 0;i < n;i++){int q,p;cin>>q>>p;if(p == 1)  q1.push_back(q);else    q2.push_back(q);}sort(q1.begin(),q1.end());sort(q2.begin(),q2.end());//题目并未保证小球坐标升序排列int l = 0, r = INF,ans = 0;while(l <= r){int mid = (l+r)/2;if(check(mid,q1,q2) >= k){r = mid-1;}else{ans = mid;l = mid+1;}}//double ans1 = ans/2;//注意这里的ans实际上是两倍的Tif(ans == INF)  cout<<"No\n";else    {ans++;cout<<"Yes\n"<<ans/2;if(ans&1)   cout<<".500000";else    cout<<".000000";//printf("Yes\n%d.%c00000\n",ans/2,"05"[ans&1]);}
}
signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);int T = 1;while(T--)solve();return 0;
}