计量经济学——空间计量概述(十八)

空间计量经济学（Spatial Econometrics）创新性地解决了经典计量方法在空间数据分析中的局限性，研究地理观测值之间的相互关系。近年来，在人文社会科学的“空间转向”背景下，空间计量已成为区域经济、房地产、环境、人口、旅游、地理、政治等领域定量研究的重要工具。空间效应本质上是一种网络效应，体现了事物之间的关联性，特别是相邻个体之间的强相关性。例如，北京的经济发展会通过邻近效应（Neighbourhood Effect）影响河北和天津的经济增长，可能导致其相对滞后。同样，地理距离不一定决定经济联系，如韩国在经济和军事上可能与美国关系更紧密，而非与其近邻中国。空间计量方法的应用可以更准确地刻画政策和市场因素的溢出效应。例如，政府的房地产限购政策不仅影响本地房价，还可能通过人口流动等因素影响周边城市的房价。如果仅使用传统面板回归（如xtreg），可能会忽略政策的间接影响。因此，空间计量方法将政策影响拆分为直接效应（对本地房价的作用）和间接效应（通过空间传播对其他城市房价的影响），从而更全面地解释政策的经济影响。

一、计量经济的数据类型

在数据分析和计量经济学中，数据主要可以分为时间序列数据（Time Series Data）、截面数据（Cross-sectional Data）和面板数据（Panel Data）。不同类型的数据具有不同的特征和分析方法。

1.1 时间序列数据（Time Series Data）

时间序列数据是按照时间顺序收集的变量观测值，通常具有时间依赖性。数据点按照等间隔时间（如天、月、年）排列，每个时间点对应一个观测值。特点如下:

• 观测值随时间变化，存在趋势、季节性、周期性或随机波动。
• 具有自相关性，即当前值可能受到过去值的影响。
• 适用于时间序列分析方法，如ARIMA、指数平滑等。

如某国1990年至2024年每年的GDP（单位：万亿美元） {15.4, 16.2, 17.0, ..., 23.8}；股票市场指数的每日收盘价，如上证指数每日收盘点位；某城市每天的空气污染指数（PM2.5）。

1.2 截面数据（Cross-sectional Data）

截面数据是指在某个特定时间点上，对多个个体（如个人、公司、国家等）进行观测的数据，通常不考虑时间维度。特点如下：

• 仅包含一个时间点的信息，无法捕捉动态变化。
• 个体之间可能存在异质性，但不涉及时间趋势。

如2024年中国各省的GDP（单位：万亿元）：{上海: 4.2, 北京: 3.8, 广东: 12.7, 四川: 6.5}；一项全国性的居民收入调查，统计不同家庭的年收入和消费情况；某一年各公司员工的薪资和学历数据。

1.3 面板数据（Panel Data）

面板数据是时间序列数据和截面数据的结合，即对多个个体在多个时间点上的观测数据。特点如下：

• 既包含时间维度，又包含个体维度，能分析数据的动态变化。
  -适用于面板数据回归模型，如固定效应模型（FE）、随机效应模型（RE）。

如2010年至2024年中国各省的GDP数据（时间 + 地区）：\(GDP_{i,t} =\{上海_{2010}: 2.1, 上海_{2024}: 4.2, 北京_{2010}: 1.9, 北京_{2024}: 3.8, ...\}\)；某企业在2015-2024年间，每年员工的工资变化情况；2010-2024年全球不同国家的失业率数据。

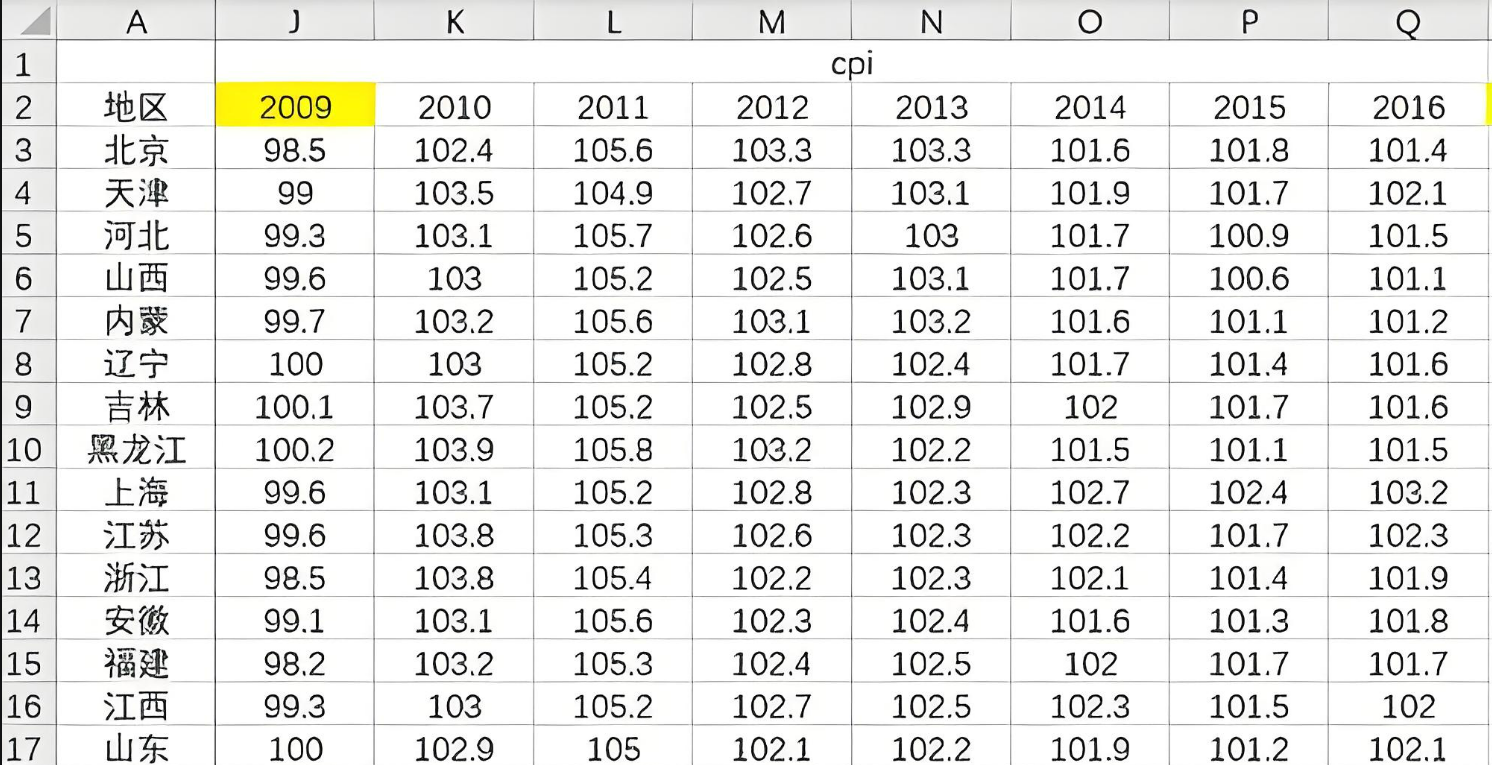
时间序列数据侧重时间维度，截面数据关注某一时点的个体差异，而面板数据结合了两者的优点，适用于更加复杂的分析。在实际应用中，不同类型的数据适用不同的统计和计量方法，以揭示数据的特征和潜在规律。

二、空间效应

空间计量经济学相较于传统计量经济学的最大区别在于引入了空间效应（Spatial Effects），这是空间计量经济学的核心特征，也是其作为独立研究领域的根本原因。空间效应主要包括空间依赖性（Spatial Dependence）和空间异质性（Spatial Heterogeneity）（Anselin, 1988）。

2.1 空间依赖性（Spatial Dependence）

空间依赖性是指个体或区域之间的相互影响，即某一区域的行为会对其邻近区域的行为产生影响。这种空间交互作用导致了截面数据的依赖性，使得传统假设的独立同分布（i.i.d.）条件不再成立。空间依赖性通常来源于地理位置的接近性，即“地理相近的个体更可能具有相似的特征”。其数学表现形式可以用空间自回归模型（SAR）或空间误差模型（SEM）来描述。例如，对于因变量 $ Y $ 的空间滞后模型（SAR），可以表示为：

\[Y = \rho WY + X\beta + \varepsilon \]

其中：

• $ W $ 是空间权重矩阵，描述了地理邻近程度；
• $ \rho $ 是空间自回归系数，衡量空间相互作用的强度；
• $ X\beta $ 为传统回归项；
• $ \varepsilon $ 是误差项。

例如，在房地产市场中，一个城市的房价不仅受当地供需关系影响，也会受到邻近城市房价变化的影响，这种相互作用就体现了空间依赖性。

2.2 空间异质性（Spatial Heterogeneity）

空间异质性指的是区域间特征的非均衡性，即不同区域的结构性差异。例如，经济发展水平、产业结构、政府政策等因素在不同地区可能存在明显差异，导致回归模型的系数因区域不同而有所变化。空间异质性通常表现为：

• 结构性不均衡：某些区域可能具有不同的经济规律，如发达地区和欠发达地区的经济增长模式不同。
• 方差异质性：不同地区的误差项方差可能不同，类似于传统计量经济学中的异方差问题。

空间异质性可以通过变系数模型（Varying Coefficient Models）或分位回归（Quantile Regression）等方法进行处理。例如，在区域经济增长分析中，东部沿海地区与西部内陆地区可能受不同的增长因素影响，这种区域差异就体现了空间异质性。

2.3 空间滞后（Spatial Lag）

与时间序列模型通过时间滞后来刻画动态关系类似，空间计量模型通过空间滞后（Spatial Lag）来刻画地理位置对变量的影响。空间滞后是某一区域变量在邻近区域的加权平均值，可以体现在因变量的滞后、自变量的滞后、误差项的滞后等多个方面。其数学表达为：

\[Y_i = \rho \sum_{j \neq i} W_{ij} Y_j + X\beta + \varepsilon \]

其中 $ W_{ij} $ 是空间权重矩阵中的元素，表示区域 $ i $ 和区域 $ j $ 之间的空间联系程度。

例如，在环境污染分析中，一个城市的空气污染水平不仅取决于当地排放量，还会受到周边城市污染扩散的影响。若某一城市的污染情况恶化，周边城市的污染水平可能也会上升，这种相互作用关系可通过空间滞后项刻画。

空间效应使得经济现象在不同区域之间具有相互影响的特性，传统的计量经济模型难以准确描述这种复杂的相互作用。空间依赖性强调变量间的相互作用，而空间异质性则反映了不同区域之间的结构性差异。在实际研究中，合理地识别和建模空间效应，有助于更准确地分析政策影响和市场变化，提高计量经济模型的解释力和预测能力。

三、空间权重矩阵（Spatial Weight Matrix）

空间权重矩阵（Spatial Weight Matrix，简称 W）是空间计量经济学中的核心工具，用于刻画区域或个体之间的空间相互作用关系。其本质是一个 $ N \times N $ 的方阵，其中 $ N $ 表示样本区域的数量，矩阵中的元素 $ W_{ij} $ 表示区域 $ i $ 和区域 $ j $ 之间的空间关联程度。

在传统回归分析中，我们通常假设观测个体之间是相互独立的，而空间计量经济学通过空间权重矩阵引入了个体之间的空间依赖关系。例如，某一地区的经济活动、房价、污染水平等可能会受到邻近地区的影响，而这些影响的强度则由 W 进行度量。

3.1 空间权重矩阵的构造方式

空间权重矩阵的构造方式多种多样，不同的方法适用于不同的研究场景。主要的构造方式包括：

基于邻接关系（Contiguity-based Weights）

• 皇后邻接权重（Queen Contiguity Weight）：若两个区域共享边界或顶点，则 $ W_{ij} = 1 $；否则 $ W_{ij} = 0 $。类似于国际象棋中的“皇后”规则，允许对角线方向上的相邻。
• 车邻接权重（Rook Contiguity Weight）：若两个区域共享边界但不共享顶点，则 $ W_{ij} = 1 $；否则 $ W_{ij} = 0 $。类似于“车”规则，仅考虑水平方向和垂直方向的相邻。

\[W = \begin{bmatrix} 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{bmatrix} \]

此矩阵表示四个区域的邻接关系，每个区域仅与相邻区域存在空间关联。

基于距离权重（Distance-based Weights）

• 反距离权重（Inverse Distance Weighting, IDW）：区域 $ i $ 和 $ j $ 之间的权重 $ W_{ij} $ 设为两者之间欧几里得距离的倒数：

  \[W_{ij} = \frac{1}{d_{ij}}, \quad i \neq j \]

  其中 $ d_{ij} $ 为两地理单元之间的距离。当距离较近时，权重较大；距离越远，权重越小。

• 距离截断权重（Threshold Distance Weight）：设定一个阈值 $ d_0 $，若 $ d_{ij} \leq d_0 $ 则 $ W_{ij} = 1 $，否则 $ W_{ij} = 0 $。

基于经济或社会联系的权重（Economic-based Weights）

• 贸易联系权重（Trade Flow Weights）：以地区间的贸易额或投资额作为权重，反映经济上的相互作用。
• 人口流动权重（Migration-based Weights）：基于地区间人口流动数据，权重矩阵的元素反映人口流动强度。

3.2 空间权重矩阵的性质

无论采用哪种构造方法，空间权重矩阵一般具有以下性质：

• 非对角性（Non-diagonal elements）：通常对角元素 $ W_{ii} = 0 $，即不考虑区域自身对自身的影响。

• 对称性（Symmetry）：某些权重矩阵满足 $ W_{ij} = W_{ji} $，即区域 $ i $ 对区域 $ j $ 的影响与区域 $ j $ 对区域 $ i $ 的影响相等（如基于距离的方法）。

• 归一化（Row-normalization）：通常对 W 进行标准化，使得每一行的和为 1：

  \[W^*_{ij} = \frac{W_{ij}}{\sum_j W_{ij}} \]

这样可以消除不同区域具有不同数量邻居的影响，使权重在不同区域间可比。

空间权重矩阵是空间计量经济学的核心工具，它提供了一种定量手段来描述区域间的空间相互作用。通过不同的构造方法，可以刻画基于邻接、距离、经济联系等多种关系的权重矩阵。在实际应用中，合理选择空间权重矩阵的形式至关重要，因为它直接影响空间计量模型的估计结果和解释力。

四、空间依赖性（Spatial Dependence）

空间依赖性（Spatial Dependence）指的是某个空间单元的观测值受到相邻或相关空间单元观测值的影响。这种依赖性在地理、经济、社会、环境等领域广泛存在。例如：

• 房价通常受相邻区域房价的影响，形成局部房价聚集现象。
• 空气污染水平可能受邻近地区的污染排放状况影响，导致污染在空间上扩散。
• 经济增长水平可能受到相邻地区经济活动的影响，如区域间贸易、基础设施共享等。

空间依赖性的存在表明，传统计量经济学假设的独立同分布（IID）条件在空间数据分析中往往无法成立，因此需要特殊的方法来识别和处理空间相关性。

4.1 空间依赖性的表现形式

空间依赖性通常表现为空间自相关（Spatial Autocorrelation），即相近空间单元的属性值存在一定程度的相关性。根据相关性的方向，空间自相关可分为：

• 正向空间自相关（Positive Spatial Autocorrelation）：相邻区域的数值趋于相似。例如，富裕地区通常邻近富裕地区，而贫困地区往往与贫困地区相邻。
• 负向空间自相关（Negative Spatial Autocorrelation）：相邻区域的数值趋于不同。例如，城市中心房价较高，而周边郊区房价较低，呈现空间上的反向分布。
• 无空间自相关（No Spatial Autocorrelation）：相邻区域的数值分布随机，未表现出明显的空间依赖性。

4.2 空间依赖性的测度方法

为了衡量空间依赖性，研究人员通常使用以下几种方法：

莫兰指数（Moran’s I）

莫兰指数（Moran’s I）是最常用的空间自相关指标，用于衡量数据在空间上的聚集程度。其计算公式如下：

\[I = \frac{N}{\sum_{i}\sum_{j} W_{ij}} \times \frac{\sum_{i}\sum_{j} W_{ij} (X_i - \bar{X})(X_j - \bar{X})}{\sum_{i} (X_i - \bar{X})^2} \]

其中：

• $ X_i $ 和 $ X_j $ 是第 $ i $ 和 $ j $ 个空间单元的观测值。
• $ \bar{X} $ 是变量的均值。
• $ W_{ij} $ 是空间权重矩阵中的元素，表示区域 $ i $ 和 $ j $ 之间的空间关联程度。
• $ N $ 为样本数量。

莫兰指数的取值范围一般在 \([-1, 1]\) 之间：

• $ I > 0 $：表示正向空间自相关，数值越大，空间聚集性越强。
• $ I < 0 $：表示负向空间自相关，数值越小，空间分布越分散。
• $ I \approx 0 $：表示空间独立，数据在空间上无明显模式。

吉尔指数（Geary’s C）

吉尔指数（Geary’s C）与莫兰指数类似，但更注重局部差异性。其计算公式为：

\[C = \frac{(N-1) \sum_{i}\sum_{j} W_{ij} (X_i - X_j)^2}{2 S_0 \sum_{i} (X_i - \bar{X})^2} \]

其中 $ S_0 = \sum_{i}\sum_{j} W_{ij} $ 是空间权重矩阵的总和。

• 若 $ C < 1 $，表示正向空间自相关。
• 若 $ C > 1 $，表示负向空间自相关。
• 若 $ C = 1 $，表示无空间自相关。

相比莫兰指数，吉尔指数对局部的空间不均衡性更加敏感。

局部空间自相关指数（LISA, Local Indicators of Spatial Association）

LISA 统计量用于识别局部空间自相关模式，如局部高值（High-High，聚集区）和局部低值（Low-Low，分散区），以及异常值（High-Low 或 Low-High）。LISA 统计量的计算方法基于莫兰指数，但应用于局部区域。

4.3 处理空间依赖性的方法

如果在分析数据时忽略空间依赖性，可能会导致回归分析的偏误，因此需要在模型中加以控制。常见的处理方法包括：

空间滞后模型（Spatial Lag Model, SLM）

在 SLM 模型中，因变量的空间滞后项被引入模型，以捕捉空间依赖性：

\[Y = \rho WY + X\beta + \varepsilon \]

其中：

• $ Y $ 是因变量，
• $ WY $ 是其空间滞后项，表示相邻区域的影响。
• $ \rho $ 是空间滞后系数，若显著不为零，则说明存在空间依赖性。
• $ X\beta $ 表示传统回归模型中的解释变量及其系数。
• $ \varepsilon $ 是误差项。

空间误差模型（Spatial Error Model, SEM）

SEM 模型用于处理误差项中的空间依赖性，模型形式为：

\[Y = X\beta + u, \quad u = \lambda Wu + \varepsilon \]

其中：

• $ u $ 为误差项，
• $ Wu $ 代表误差的空间滞后项。
• $ \lambda $ 是空间误差系数，若显著不为零，则表明误差项具有空间相关性。

地理加权回归（GWR, Geographically Weighted Regression）

GWR 允许回归系数随空间位置变化，从而适应不同区域之间的异质性。其回归模型形式为：

\[Y_i = \beta_0(u_i, v_i) + \sum_{k} \beta_k(u_i, v_i) X_{ik} + \varepsilon_i \]

其中 $ (u_i, v_i) $ 代表空间坐标。GWR 适用于分析变量影响因子的空间差异性，如房价对收入的弹性在不同城市可能不同。

五、应用案例

考虑房价与家庭收入对犯罪率的作用来探究空间计量模型的应用，数据集包含美国俄亥俄洲哥伦布市49个社区编号(id)、犯罪率(crime)、房价(hoval)、家庭收入(income)、经度(x)和纬度(y)。数据下载连接:https://wwxh.lanzouv.com/ivpVa2mcjaab，压缩文件中10-8.xlsx是数据文件，10-8w.xlsx是这49个社区地理位置为基础的二进制邻接空间权重矩阵。

5.1 普通的最小二乘回归

import pandas as pd
import statsmodels.api as sm
import os# 1. 设置桌面路径并读取 Excel 文件
desktop_path = os.path.join(os.path.expanduser("~"), "Desktop")  # 获取桌面路径
file_path = os.path.join(desktop_path, "10-8.xlsx")  # 目标文件路径# 读取 Excel 文件
df = pd.read_excel(file_path)# 2. 检查数据结构
print("数据概览：")
print(df.head())  # 显示前几行数据# 3. 确保所需变量存在
required_columns = ["crime", "hoval", "income"]
for col in required_columns:if col not in df.columns:raise ValueError(f"数据缺少必要变量: {col}")# 4. 定义回归变量
y = df["crime"]  # 因变量
X = df[["hoval", "income"]]  # 自变量
X = sm.add_constant(X)  # 添加常数项（截距）# 5. 进行 OLS 回归
model = sm.OLS(y, X).fit()# 6. 输出回归结果（类似 EViews 格式）
print(model.summary())

数据概览：id      hoval  income      crime      x       y
0   1  44.567001  21.232  18.801754  8.310  13.996
1   2  33.200001   4.477  32.387760  8.444  13.724
2   3  37.125000  11.337  38.425858  8.417  13.372
3   4  75.000000   8.438   0.178269  8.130  13.292
4   5  80.467003  19.531  15.725980  8.830  14.369OLS Regression Results                            
==============================================================================
Dep. Variable:                  crime   R-squared:                       0.552
Model:                            OLS   Adj. R-squared:                  0.533
Method:                 Least Squares   F-statistic:                     28.39
Date:                Thu, 30 Jan 2025   Prob (F-statistic):           9.34e-09
Time:                        23:06:53   Log-Likelihood:                -187.38
No. Observations:                  49   AIC:                             380.8
Df Residuals:                      46   BIC:                             386.4
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==============================================================================coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         68.6190      4.735     14.490      0.000      59.087      78.151
hoval         -0.2739      0.103     -2.654      0.011      -0.482      -0.066
income        -1.5973      0.334     -4.780      0.000      -2.270      -0.925
==============================================================================
Omnibus:                        2.771   Durbin-Watson:                   1.193
Prob(Omnibus):                  0.250   Jarque-Bera (JB):                1.836
Skew:                          -0.273   Prob(JB):                        0.399
Kurtosis:                       3.775   Cond. No.                         130.
==============================================================================

显然房价hoval和家庭收入income对犯罪率crime有显著负向影响。

5.2 空间相关性检验

引入空间权重矩阵文件10-8w.xlsx，进行空间相关性分析。

import pandas as pd
import numpy as np
import libpysal as ps
import geopandas as gpd
import matplotlib.pyplot as plt
from esda.moran import Moran
from splot.esda import moran_scatterplot
import os# **1. 获取桌面路径**
desktop_path = os.path.join(os.path.expanduser("~"), "Desktop")# **2. 文件路径**
data_file = os.path.join(desktop_path, "10-8.xlsx")  # 主要数据
weight_file = os.path.join(desktop_path, "10-8w.xlsx")  # 空间权重矩阵# **3. 读取 10-8.xlsx（不跳过第一行）**
df = pd.read_excel(data_file)# **4. 读取 10-8w.xlsx**
w_matrix = pd.read_excel(weight_file, header=0)  # 第一行作为列名# **5. 构建 PySAL 空间权重对象**
w = ps.weights.util.full2W(w_matrix.fillna(0).to_numpy())  # NaN 替换为 0
w.transform = 'r'  # 归一化权重# **6. 计算 Moran’s I**
y = df["crime"]
moran = Moran(y, w)# **7. 计算标准差（替换 seI）**
std_error = np.sqrt(moran.VI_norm)# **8. 输出 Moran’s I 结果**
print("\n=== 📌 Moran’s I 统计量 ===")
print(f"Moran’s I: {moran.I:.4f}")
print(f"期望值 E(I): {moran.EI:.4f}")
print(f"标准差: {std_error:.4f}")  # 修改这里
print(f"z-score: {moran.z_norm:.4f}")
print(f"p-value: {moran.p_norm:.4f}")# **9. Moran 散点图**
fig, ax = moran_scatterplot(moran)
plt.show()

=== 📌 Moran’s I 统计量 ===
Moran’s I: 0.5110
期望值 E(I): -0.0208
标准差: 0.0937
z-score: 5.6754
p-value: 0.0000

1️⃣ Moran’s I = 0.5110

• Moran’s I 指标的取值范围通常在 [-1,1] 之间：
  • I > 0 表示正的空间自相关，即相似的值（高值或低值）在空间上聚集在一起。
  • I < 0 表示负的空间自相关，即高值和低值交错分布。
  • I ≈ 0 表示无空间自相关，即变量在空间上随机分布。
• 你的 I 值为 0.5110，接近 1，表明存在较强的正空间自相关，即相邻地区的 crime 值存在聚集现象（高犯罪率地区倾向于聚集在一起，低犯罪率地区也是如此）。

2️⃣ 期望值 E(I) = -0.0208

• E(I) 为在“无空间自相关”（即随机分布）的情况下 Moran’s I 的理论期望值。
• 由于 E(I) 接近 0 且为负数，表明在随机分布假设下，Moran’s I 期望值稍微偏负。

3️⃣ 标准差 = 0.0937

• Moran’s I 统计量的标准误差（standard deviation），用于计算 z-score。

4️⃣ z-score = 5.6754

• z-score 衡量 Moran’s I 偏离期望值的程度： z=I−E(I)标准差z = \frac{I - E(I)}{\text{标准差}}z=标准差I−E(I)​
  • 如果 z-score 绝对值大于 1.96（95% 置信水平）或大于 2.58（99% 置信水平），可以认为空间自相关显著。
  • 你的 z-score = 5.6754，远远大于 2.58，表明空间自相关极其显著。

5️⃣ p-value = 0.0000

• p-value 反映显著性水平：
  • p < 0.05：拒绝原假设，认为存在空间自相关。
  • p < 0.01：高度显著的空间自相关。
  • p ≈ 0.0000，说明结果极其显著，拒绝“无空间自相关”的原假设，说明数据确实具有正的空间自相关性。

📌 计量统计结论

• 你的数据存在显著的正空间自相关，即犯罪率高的地区往往邻近于其他高犯罪率地区，低犯罪率地区也是如此。
• 由于 z-score 远大于 2.58 且 p-value 接近 0.0000，说明这种空间聚集模式并非随机发生，而是高度显著的现象。
• 这表明，在你分析的 49 个社区中，crime 变量在空间上的分布并不是随机的，而是存在聚集效应（可能受到地理位置、社会经济因素的影响）。

5.3 空间模型分析

import os
import pandas as pd
import numpy as np
import pysal.lib
from pysal.lib import weights
from spreg import OLS, ML_Lag, ML_Error# 📂 读取数据文件
desktop_path = os.path.join(os.path.expanduser("~"), "Desktop")  # 获取桌面路径
data_file = os.path.join(desktop_path, "10-8.xlsx")  # 数据文件
weight_file = os.path.join(desktop_path, "10-8w.xlsx")  # 空间权重矩阵# 📊 读取数据
df = pd.read_excel(data_file)  # 读取完整数据
print(f"✅ 读取数据成功，数据维度: {df.shape}")# 选择回归变量
y = df['crime'].values.reshape(-1, 1)  # 因变量
X = df[['hoval', 'income']].values  # 自变量
X = np.hstack([np.ones((X.shape[0], 1)), X])  # 添加常数项（截距）# 🗺️ 读取空间权重矩阵（不读取第一行）
w_df = pd.read_excel(weight_file, header=0)
w_matrix = w_df.values
assert w_matrix.shape == (49, 49), f"⚠️ 读取的权重矩阵维度错误！当前为 {w_matrix.shape}，应为 (49, 49)"
print(f"✅ 读取空间权重矩阵成功，维度: {w_matrix.shape}")# 转换为 PySAL 格式
w = weights.util.full2W(w_matrix)  # 转换为权重对象
w.transform = 'r'  # 归一化权重矩阵（行标准化）# ==================== 📌 OLS 估计 ====================
print("\n=== 📌 OLS 线性回归估计 ===")
ols_model = OLS(y, X, name_y="crime", name_x=['constant', 'hoval', 'income'])
print(ols_model.summary)# ==================== 📌 SLM 估计 ====================
print("\n=== 📌 空间滞后模型 (SLM) ===")
slm_model = ML_Lag(y, X, w, name_y="crime", name_x=['constant', 'hoval', 'income'])
print(slm_model.summary)# ==================== 📌 SEM 估计 ====================
print("\n=== 📌 空间误差模型 (SEM) ===")
sem_model = ML_Error(y, X, w, name_y="crime", name_x=['constant', 'hoval', 'income'])
print(sem_model.summary)

1️⃣ OLS 线性回归结果

• 回归方程： $$crime=68.62−0.274×hoval−1.597×income$$

• R² = 0.5524，表明模型解释了 55.24% 的 crime 变量变异。

• F 统计量 = 28.3856，p = 0.0000，表明整体回归显著。

• 解释变量显著性：

  • hoval（住房价值）：系数 -0.2739，p = 0.01087，说明住房价值较高的地区，犯罪率较低（显著）。
  • income（收入）：系数 -1.5973，p = 0.00002，说明高收入地区犯罪率较低（显著）。

• Jarque-Bera 检验（JB）p = 0.3994，表明误差项符合正态分布，适用于 OLS。

• Breusch-Pagan 检验（BP）p = 0.0193，说明存在异方差性问题，OLS 估计可能有偏。

• 多重共线性：条件数 6.542，低于 10，不严重。

• hoval 和 income 都显著影响 crime，但 OLS 可能忽略了空间相关性，导致误差项有空间依赖。

2️⃣ 空间滞后模型（SLM）

• 回归方程： $$\text{crime} = 45.08 - 0.266 \times \text{hoval} - 1.032 \times \text{income} + 0.431 \times W_{\text{crime}}​$$

• ρ（空间滞后系数）= 0.431，p = 0.00025，表明 crime 变量具有空间自相关性，即高犯罪率地区的犯罪率会影响周围地区。

• R²（伪）= 0.6523，比 OLS 提高，说明加入空间因素提高了模型解释能力。

• 解释变量显著性：

  • hoval（住房价值）：系数 -0.2659，p = 0.00266，影响与 OLS 结果类似（但略微降低）。
  • income（收入）：系数 -1.0316，p = 0.00072，影响与 OLS 类似，但系数略小。

• 直接效应、间接效应、总效应：

  • hoval 的总影响 -0.4674（包括直接 -0.2659 和空间间接 -0.2015），说明住房价值影响了周边地区犯罪率。
  • income 的总影响 -1.8131，说明高收入不仅影响自身地区犯罪率，也影响周边。

• 空间滞后效应明显，犯罪率不仅受自身经济因素影响，还受邻近地区影响。

• 该模型更适合描述 crime 变量的空间扩散效应。

3️⃣ 空间误差模型（SEM）

• 回归方程： $$crime=59.89−0.302×hoval−0.941×income+u$$

• 误差项： $$u=0.5618×Wu+ϵ$$

• λ（空间误差系数）= 0.5618，p = 0.00003，表明误差项存在空间相关性，可能遗漏了影响 crime 的空间因素。

• 伪 R² = 0.5357，略低于 SLM，但比 OLS 仍然更优。

• 解释变量显著性：

  • hoval：系数 -0.3022，p = 0.00084，影响比 OLS 更强。
  • income：系数 -0.9413，p = 0.00441，影响比 OLS 更小。

• 误差项的空间依赖性显著，表明可能遗漏了一些重要的空间变量（如社会环境、警力分布等）。

• 适用于研究误差项的空间相关性，而非变量的空间扩散效应。

4️⃣ 模型比较

模型	R² / 伪 R²	空间效应	影响方式	空间参数	AIC（越小越优）
OLS	0.5524	❌ 无	线性关系	无	380.754
SLM	0.6523	✅ 有	直接 & 邻近	ρ = 0.431	372.781
SEM	0.5357	✅ 有	误差空间扩散	λ = 0.5618	372.761

📌 关键结论

• 住房价值（hoval）和收入（income）均显著影响犯罪率：

  • 住房价值越高，犯罪率越低（可能由于社区管理和经济条件）。
  • 收入越高，犯罪率越低（经济状况较好，犯罪动机减少）。

• 犯罪率具有空间相关性：

  • SLM 显示 ρ = 0.431，即高犯罪率地区会影响邻近地区。
  • SEM 显示 λ = 0.5618，表明误差项也存在空间相关性，可能遗漏了影响 crime 的空间因素（如社会治安）。

• 空间模型（SLM、SEM）更优于 OLS：

  • SLM 更适合研究犯罪的空间扩散模式。
  • SEM 适合研究误差项的空间相关性。

• 可以使用更复杂的空间杜宾模型（SDM），同时考虑空间滞后和误差相关性，进一步优化模型。

总结

空间依赖性是空间计量经济学的重要特征，广泛存在于经济、社会、环境等数据分析领域。空间自相关的存在表明，传统的回归分析方法可能无法准确估计模型参数，因此需要采用如莫兰指数、吉尔指数等统计方法来识别空间依赖性，并采用空间回归模型（SLM、SEM）或地理加权回归（GWR）来合理建模。通过合理控制空间依赖性，可以提高模型的解释力和预测精度，为空间数据分析提供更准确的定量依据。

参考资料

1. 空间截面数据与空间面板数据计量模型全套解读
2. “傻瓜”学计量——时空分异分析）
3. 空间计量模型选择、估计、权重、检验(Spatial effect)