AP Physics C Mechanics Chapter 7 Rotation 1

Vocabulary

• Rigid body 刚体
• Angular displacement 角位移 \(\Delta \theta\)
• Angular velocity 角速度 \(\omega\)
• Angular acceleration 角加速度 \(\alpha\)
• Rotational kinetic energy 旋转动能 \(KE_{\text{rotational}}\)
• Rotational inertia 转动惯量 \(I\)
• Torque 扭矩 \(\tau\)

Angular Quantities

Angular displacement:

\[\boxed{\Delta \theta = \theta_{\text{final}} - \theta_{\text{initial}}} \]

Angular velocity:

\[\boxed{\omega = \frac {d \theta} {dt}} \]

Angular acceleration:

\[\boxed{\alpha = \frac {d \omega} {dt} = \frac {d^2 \theta} {dt^2}} \]

Equations

Valid only for uniformly accelerated motion (UAM):

\[\omega = \omega_0 + \alpha t \]

\[\omega^2 = \omega_0^2 + 2 \alpha \Delta \theta \]

Relationships Between Angular and Linear Quantities

Differentiate both sides of \(s = r \theta\) with respect to \(t\):

\[\boxed{v = r \omega} \]

Differentiate both sides again:

\[\boxed{a_{\text{tan}} = r \alpha} \]

---

In Chapter 3 we derived:

\[\boxed{a_{\text{radial}} = \frac {v^2} r = r \omega^2} \]

Translational KE \(\to\) Rotational KE

Divide the object into infinitely small pieces and sum the KE of each piece:

\[\begin{aligned}KE_{\text{rotational}} &= \int \frac 1 2 v^2 dm \\&= \frac 1 2 \int r^2 \omega^2 dm \\&= \frac 1 2 \omega^2 \int r^2 dm \\ \end{aligned}\]

This equation is very similar to \(KE = \frac 1 2 m v^2\), which is the equation for translational KE. \(\int r^2 dm\) is the angular analog of mass.

Just as mass is a measure of translational inertia, this integral is a measure of rotational inertia:

\[\boxed{I = \int r^2 dm} \]

(Which is the definition of rotational inertia)

We can rewrite the equation for rotational kinetic energy:

\[\boxed{KE_{\text{rotational}} = \frac 1 2 I \omega^2} \]

Example: Thin Rod

https://zhuanlan.zhihu.com/p/469279301

\[\begin{aligned}I &= \int r^2 dm \\&= \int_0^L r^2 \times \rho \times dr \\&= \frac 1 3 \rho L^3 \\&= \frac 1 3 m L^2 \\ \end{aligned}\]

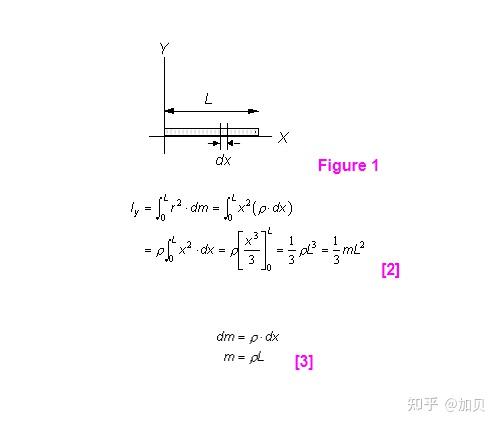
Force \(\to\) Torque

We are expecting a rotational analog of \(\vec F = m \vec a\), so we start from the expression \(I \alpha\):

\[\begin{aligned}& I \alpha \\=& \int r^2 \alpha dm \\=& \int r a_{\tan} dm \\=& \int r dF_{\tan} \\=& r \times F_{\tan} \\ \end{aligned}\]

Therefore, it is very natural to define torque \(\tau\) as:

\[\tau = r F_{\tan} = r F \sin \theta \]

\[\boxed{\vec{\tau} = \vec{r} \times \vec{F}} \]

(A cross product!)

And we have the Newton's second law for rotational motion:

\[\boxed{\tau_{\text{net}} = I \alpha} \]

The unit of torque is newton meters (which is the same as joule), but it doesn't mean that torque is a kind of energy.

https://physics.stackexchange.com/questions/37881/why-is-torque-not-measured-in-joules

Fun fact: alternative units for torque are Joules/radian, though not heavily used.

This can be shown in the following part.

Work Done by an External Force

\[\begin{aligned}& dW \\=& \vec{F} \cdot d\vec{r} \\=& F_{\tan} \cdot d\vec{r} \\=& F_{\tan} \cdot r \cdot d\theta \\=& \tau d\theta \\ \end{aligned}\]

We've got the expression of work in rotational systems:

\[\boxed{dW = \tau d\theta \Leftrightarrow W = \int \tau d\theta \xlongequal{\text{const } \tau} \tau \Delta \theta} \]

Potential Energy

\[\begin{aligned}& \tau \\=& \frac {dW} {d\theta} \\=& \frac {dKE} {d\theta} \\=& -\frac {dU} {d\theta} \\ \end{aligned}\]

Using the above arguments, we can relate torque to potential energy (valid only if the torque is produced by conservative forces):

\[\boxed{\tau = - \frac {dU} {d\theta}} \]

Power

\[\begin{aligned}& P \\=& \frac {dW} {dt} \\=& \tau \frac {d\theta} {dt} \\=& \tau \omega \\ \end{aligned}\]

Now we can relate power in rotational systems:

\[\boxed{P = \tau \omega} \]