「作业」2025/2/3 线性筛素数

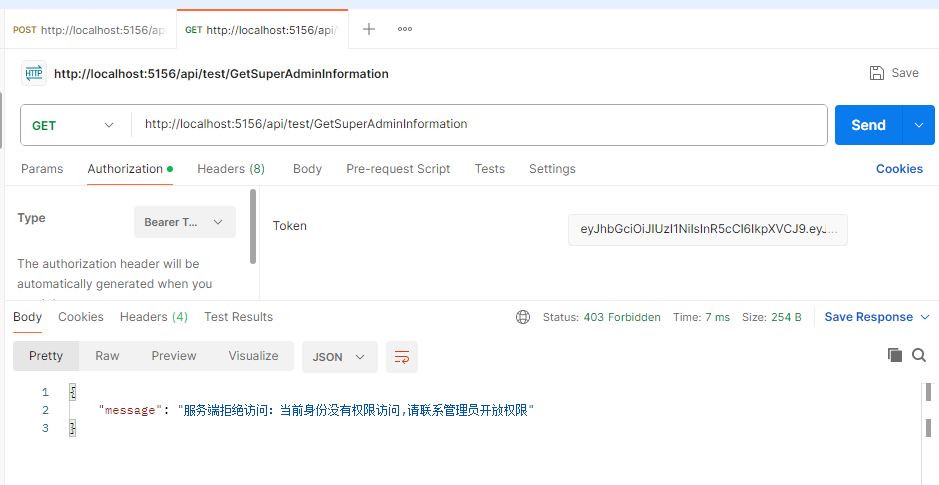
A. 【模板】线性筛素数

传送门：水滴

线性筛板子。原理请看这个。

点击查看代码

#include <bits/stdc++.h>
#define ll long longusing namespace std;const int maxn = 1e8 + 10;int prime[maxn];
bool isPrime[maxn];void xxs (ll n) {int cnt = 0;memset (isPrime, 1, sizeof(isPrime));isPrime[1] = 0;for (int i = 2; i <= n; i++) {if (isPrime[i]) prime[++cnt] = i;for (int j = 1; j <= cnt && i * prime[j] <= n; j++) {isPrime[i * prime[j]] = 0;if (i % prime[j] == 0)break;}}
}int n, q;int main(){scanf("%d%d", &n, &q);xxs (n);while (q--) {int k; scanf("%d", &k);printf("%d\n", prime[k]);} return 0;
}

---

B. A % B Problem

传送门：水滴

题目大意：给定正整数 $l, r$，求区间 $[l, r]$ 中质数的个数。

首先写好线性筛板子。看到 $l, r$ 想到预处理质数数的前缀和。设 ans[i] 表示第 $i$ 个数中有多少质数。分两种情况：

• 第 $i$ 个数是合数，就把 ans[i] 赋值为 ans[i - 1]，没有对答案造成贡献。

• 第 $i$ 个数是质数，就把 ans[i] 赋值为当前质数的个数。

最后判断一下边界情况，如果合法就输出 ans[r] - ans[l - 1] 即可。

点击查看代码

#include <bits/stdc++.h>
#define ll long longusing namespace std;const int maxn = 1e6 + 10;int n, m;
int l, r;int prime[maxn];
bool isPrime[maxn];
int ans[maxn];inline void xxs(int n) {int cnt = 0;memset(isPrime, 1, sizeof(isPrime));isPrime[1] = 0;for (int i = 2; i <= n; i++) {ans[i] = ans[i - 1];if (isPrime[i])prime[++cnt] = i, ans[i] = cnt;for (int j = 1; j <= cnt && i * prime[j] <= n; j++) {isPrime[i * prime[j]] = 0;if (i % prime[j] == 0)break;}}
}int main(){scanf("%d%d", &n, &m);xxs(m);while (n--) {scanf("%d%d", &l, &r);if (l > m || l < 1 || r > m || r < 1) printf("Crossing the line\n");else printf("%d\n", ans[r] - ans[l - 1]);}return 0;
}