2025省选模拟9

2025省选模拟9

网络流专场是吧😅

Delov 的 npy 们 原题链接

一眼网络流，然后不会了。

发现正常顺着限制做做不了，考虑将限制转化一下，以 L 操作为例。

在 \(a_i\) 左侧的点中不超过 \(b_i\) 个，等价于从左往右数第 \(b_i+1\) 个点在 \(a_i\) 右侧。

但还是不好做，考虑枚举选择的点的个数，这样就可以知道选择的第 \(i\) 个点应该所处的区间。

然后就是网络流经典操作——拆点。

将一个点拆成两个点，一个为横坐标，一个为纵坐标，中间连边容量为 \(1\)，费用为 \(w\)，如果横坐标在第 \(i\) 个点可以的范围内，那么就将该点和横坐标和第 \(i\) 个点连边，如果纵坐标在第 \(i\) 个点范围内，那么就将该点的纵坐标与第 \(i\) 个点相连。

说的不太好，还是看图吧。

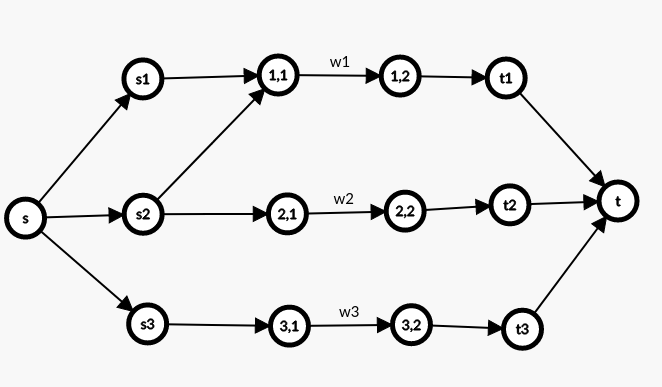
容量都为 \(1\)，若非标注，则费用为 \(0\)。

\(s\) 是超级源点，\(sk\) 表示横坐标第 \(k\) 个点，\((i,1/2)\) 表示第 \(i\) 个点拆点， \(tk\) 表示纵坐标第 \(k\) 个点，\(t\) 为超级汇点。

再不懂就自行理解吧，语文不好，实在不会说了。

code

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALauto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#elseauto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
#define ep emplace
const int N = 100010;
int a[N],b[N],c[N],d[N],x[N],y[N],n,m;
int s,t;ll w[N];
template<size_t N,size_t M>
struct Graph{struct E{int to,n,w;ll c;}e[M];int h[N],ct = 1;void add(int u,int v,int w,ll c){e[++ct] = {v,h[u],w,c};h[u] = ct;}void clear(){ct = 1;rep(i,0,N-1,1) h[i] = 0;}
#define repe(i,x,y,g) for(int i = g.h[x],y = g.e[i].to;i;i = g.e[i].n,y = g.e[i].to)
};Graph<N,N> g;
ll dist[N];bool vis[N];int now[N];
bool bfs(int s = s){rep(i,s,t,1) dist[i] = -1e18,vis[i] = false,now[i] = g.h[i];queue<int> q;q.ep(s);vis[s] = true;dist[s] = 0;while(q.size()){int x = q.front();q.pop();vis[x] = false;repe(i,x,y,g){int w = g.e[i].w;ll c = g.e[i].c;if(!w) continue;if(dist[y] < dist[x] + c){dist[y] = dist[x] + c;if(!vis[y]) vis[y] = true,q.ep(y);}}}return dist[t] != -1e18;
}
int dinic(int x,int flow){if(x == t || !flow) return flow;int res = 0;vis[x] = true;for(int i = now[x];i && flow;i = g.e[i].n){now[x] = i;int w = g.e[i].w,y = g.e[i].to;ll c = g.e[i].c;if(!w) continue;if(vis[y]) continue;if(dist[y] == dist[x] + c){int k = dinic(y,min(flow,w));g.e[i].w -= k;g.e[i^1].w += k;res += k;flow -= k;}}return res;
}
pair<int,ll> MaxCostFlow(){int maxflow = 0;ll maxcost = 0;while(bfs()){int k = dinic(s,1e9);maxflow += k;maxcost += dist[t]*k;}return make_pair(maxflow,maxcost);
}
ll calc(int k){g.clear();s = 0,t = 2*k+2*n+1;rep(i,1,k,1){g.add(s,i,1,0);g.add(i,s,0,0);g.add(i+2*n+k,t,1,0);g.add(t,i+2*n+k,0,0);}rep(i,1,n,1){g.add(i+k,i+k+n,1, w[i]);g.add(i+k+n,i+k,0,-w[i]);rep(j,1,k,1){if(a[j] <= x[i] && x[i] <= b[k-j+1]) g.add(j,i+k,1,0),g.add(i+k,j,0,0);if(c[j] <= y[i] && y[i] <= d[k-j+1]) g.add(i+k+n,j+k+n*2,1,0),g.add(j+k+n*2,i+k+n,0,0);}}return MaxCostFlow().second;
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);memset(b,0x3f,sizeof b);memset(d,0x3f,sizeof d);cin>>n;rep(i,1,n,1) cin>>x[i]>>y[i]>>w[i];cin>>m;rep(i,1,m,1){char op;int x,y;cin>>op>>x>>y;y++;if(op == 'L') a[y] = max(a[y],x+1);if(op == 'R') b[y] = min(b[y],x-1);if(op == 'D') c[y] = max(c[y],x+1);if(op == 'U') d[y] = min(d[y],x-1);}rep(i,1,n,1) a[i] = max(a[i],a[i-1]),b[i] = min(b[i],b[i-1]),c[i] = max(c[i],c[i-1]),d[i] = min(d[i],d[i-1]);ll ans = 0;rep(i,0,n,1) ans = max(ans,calc(i));cout<<ans<<'\n';
}

皮胚 原题链接

以 popcount 的奇偶性分组，然后发现就变成了二分图了。

但是点数是 \(O(2^n)\) 的，边数是 \(O(n\times 2^n)\) 的，显然过不了，考虑缩小点的数量和边的数量。

我们发现每个点会与 \(n\) 个人相连，那么每匹配一对就会让剩下匹配的方案数最多减少 \(2\times (n−1)\)（这两个人都不能与他另外 \(n−1\) 个与其仅有一个观点不同的人匹配），加上这两个人匹配的这条边总共减少\(2\times n−1\)，所以说假如匹配 \(k\) 次最多只会减少 \(k\times (2\times n−1)\) 种匹配方式，也就是假如选择 \(k\times(2\times n−1)\) 个匹配那么至少会存在 \(k\) 种匹配方式。

那么只需要取前 \(k\times (2\times n-1)\) 条边即可。用 std::nth_element 可以在 \(O(n)\) 的时间求出。

然后跑二分图最大权匹配就行。

但是常规的二分图最大权匹配要将左部点和汇点连一条边，本题因为有特殊性质所以不用。（特殊性质是两点之间的边权为两点点权和，为什么不用自行思考）

code

#include<bits/stdc++.h>
using namespace std;
#define rep(i,s,t,p) for(int i = s;i <= t;i += p)
#define drep(i,s,t,p) for(int i = s;i >= t;i -= p)
#ifdef LOCALauto I = freopen("in.in","r",stdin),O = freopen("out.out","w",stdout);
#elseauto I = freopen("pp.in","r",stdin),O = freopen("pp.out","w",stdout);//auto I = stdin,O = stdout;
#endif
using ll = long long;using ull = unsigned long long;
using db = double;using ldb = long double;
#define ppc __builtin_popcount
#define ep emplace
const int N = 1e6 + 60000,M = 1e5;
template<size_t N,size_t M>
struct Graph{struct E{int to,n;ll w,c;}e[M];int h[N],ct = 1;void add(int u,int v,ll w,ll c){e[++ct] = {v,h[u],w,c};h[u] = ct;}
#define repe(i,x,y,g) for(int i = g.h[x],y = g.e[i].to; i;i = g.e[i].n,y = g.e[i].to)
};Graph<N,M> g;
int n,k,a[N],tot,ttt,s,t,_s,bel[N];
struct node{int v,x,y;}edge[N*20];
int now[N];ll dist[N];bool vis[N];
bool bfs(int s = s){rep(i,1,tot,1) dist[i] = -1e18,now[i] = g.h[i],vis[i] = false;queue<int> q;q.push(s);vis[s] = true;dist[s] = 0;while(q.size()){int x = q.front();q.pop();vis[x] = false;repe(i,x,y,g){auto w = g.e[i].w,c = g.e[i].c;if(!w) continue;if(dist[y] < dist[x] + c){dist[y] = dist[x] + c;if(!vis[y]) q.ep(y),vis[y] = true;}}}return dist[t] != -1e18;
}
int dinic(int x,int flow){if(x == t || !flow) return flow;ll res = 0;vis[x] = true;for(int i = now[x]; i&&flow;i = g.e[i].n){now[x] = i;int y = g.e[i].to,w = g.e[i].w;ll cost = g.e[i].c;if(!w) continue;if(vis[y]) continue;if(dist[y] == dist[x] + cost){int k = dinic(y,min(flow,w));g.e[i].w -= k;g.e[i^1].w += k;res += k;flow -= k;}}return res;
}
pair<int,ll> MaxCostFlow(){int maxflow = 0;ll maxcost = 0;while(bfs()){ll k = dinic(s,1e9);if(!k) break;maxflow += k;maxcost += dist[t]*k;}return make_pair(maxflow,maxcost);
}
signed main(){cin.tie(nullptr)->sync_with_stdio(false);cin>>n>>k;rep(i,0,(1<<n)-1,1) cin>>a[i];rep(i,0,(1<<n)-1,1){rep(j,0,n-1,1){int p = i^(1<<j);if(p >= i) continue;edge[++ttt] = (node){a[i]+a[p],i,p};}}s = ++tot,t = ++tot,_s = ++tot;g.add(s,_s,k,0);g.add(_s,s,0,0);int req = k*(2*n-1);if(req > ttt) req = ttt;nth_element(edge+1,edge+1+req,edge+1+ttt,[](const node &x,const node &y){return x.v > y.v;});rep(i,1,req,1){auto p = edge[i];if(ppc(p.x)%2 == 0) swap(p.x,p.y);if(!bel[p.x]) bel[p.x] = ++tot,g.add(_s,bel[p.x],1,0),g.add(bel[p.x],_s,0,0);if(!bel[p.y]) bel[p.y] = ++tot,g.add(bel[p.y],t,1,0),g.add(t,bel[p.y],0,0);g.add(bel[p.x],bel[p.y],1, p.v);g.add(bel[p.y],bel[p.x],0,-p.v);}cout<<MaxCostFlow().second<<'\n';
}

流（flow） 原题链接

不会，不想打了。

今天是春日野穹生日捏。

p