堆
堆可以看作一颗完全二叉树的数组对象。
特性:
1.堆是完全二叉树,除了树最后一层不需要满,其余层次都需要满,如果最后一层不是满的,那么要求左满右不满

2.通常使用数组实现,将二叉树结点依次放入数组中,根结点再位置1,子结点在2和3,子结点的子结点在4,5,6,7,以此类推。
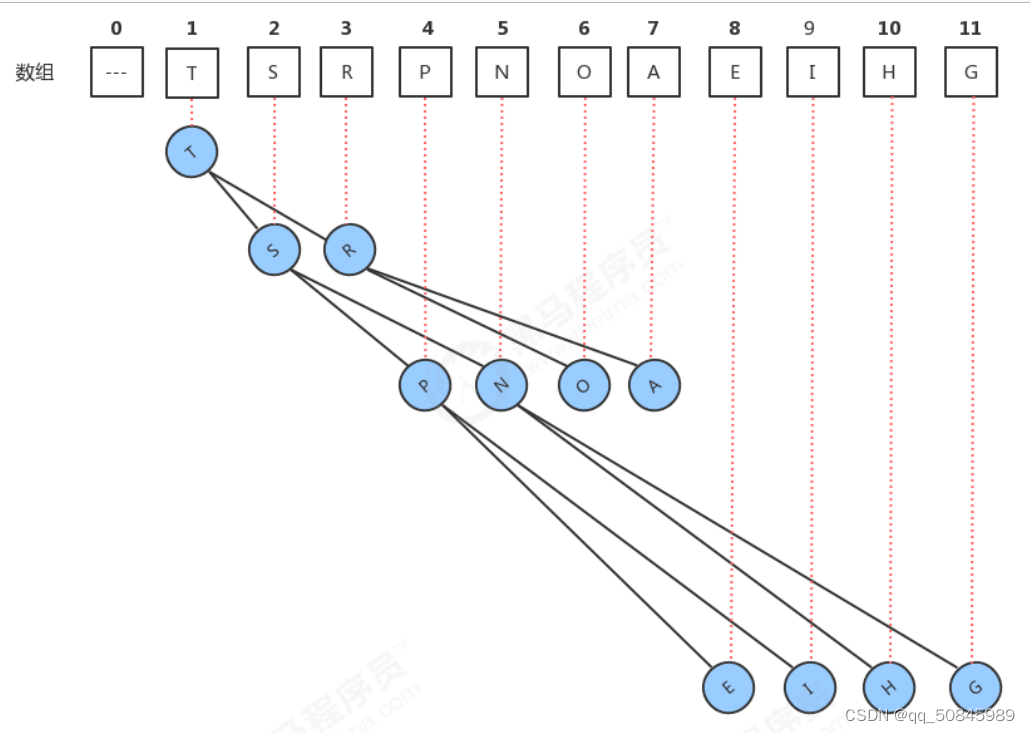
如果结点位置为k,父节点位置为k/2,子结点分别是2k和2k+1。
3.每个结点大于等于子节点,两个子结点顺序未安排。
元素上浮下沉:
//使用上浮算法,使索引k处的元素能在堆中处于一个正确的位置
private void swim(int k){
//如果已经到了根结点,就不需要循环了
while(k>1){
//比较当前结点和其父结点
if(less(k/2,k)){
//父结点小于当前结点,需要交换
exch(k/2,k);
}
k = k/2;
}
}//使用下沉算法,使索引k处的元素能在堆中处于一个正确的位置
private void sink(int k){
//如果当前已经是最底层了,就不需要循环了
while(2*k<=N){
//找到子结点中的较大者
int max;
if (2*k+1<=N){//存在右子结点
if (less(2*k,2*k+1)){
max = 2*k+1;
}else{
max = 2*k;
}
}else{//不存在右子结点
max = 2*k;
}
//比较当前结点和子结点中的较大者,如果当前结点不小,则结束循环
if (!less(k,max)){
break;
}
//当前结点小,则交换,
exch(k,max);
k = max;
}
}
}堆构造:
创建一个新数组,将原数组0~length-1的数据拷贝到新数组1~length处,从新数组长度的一般开始往索引1处扫描(从右往左),对每个元素进行下沉处理。
堆排序:
在构造好的堆上进行:
1.交换堆顶元素和最大索引处元素,代表最大和最小
2.下沉堆顶元素,忽略最大索引处的最大元素,范围是【1,N-执行次数】
3.重复1和2步骤,直到范围变成【1,1】
int N = heap.length-1;
while(N!=1){
//3.2交换heap中索引1处的元素和N处的元素
exch(heap,1,N);
N--;
//3.3对索引1处的元素在0~N范围内做下沉操作
sink(heap,1,N);
}
//在heap堆中,对target处的元素做下沉,范围是0~range
private static void sink(Comparable[] heap, int target, int range){
//没有子结点了
while (2*target<=range){
//1.找出target结点的两个子结点中的较大值
int max=2*target;
if (2*target+1<=range){
//存在右子结点
if (less(heap,2*target,2*target+1)){
max=2*target+1;
}
}
//2.如果当前结点的值小于子结点中的较大值,则交换
if(less(heap,target,max)){
exch(heap,target,max);
}
//3.更新target的值
target=max;
}
}
}