题目链接
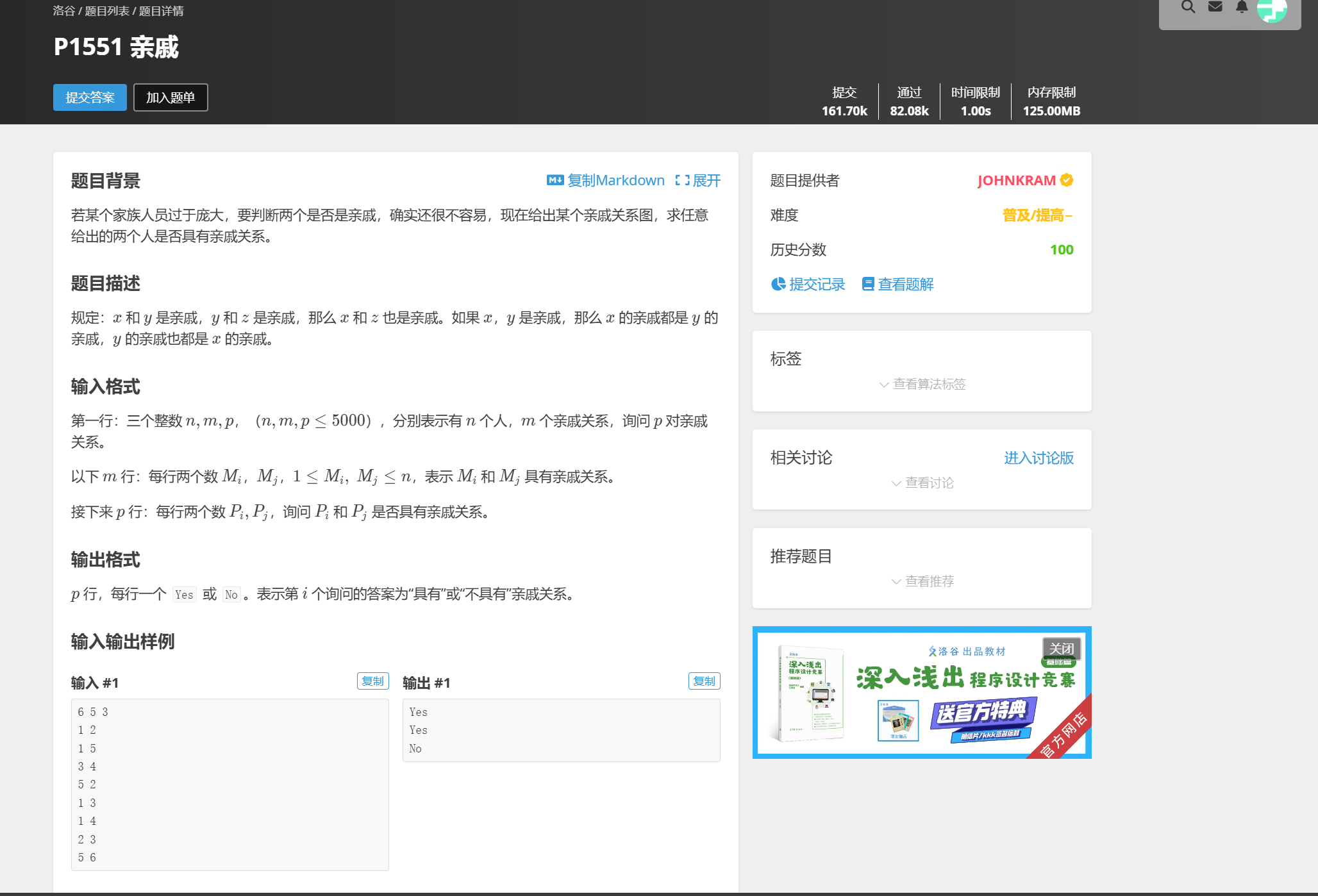
题意:推箱子。给定一个 \(n \times m\) 的长方形地面,上面有若干障碍物,并给定箱子与人的位置,问哪些位置可以被人用箱子推到。
显然,对于一个局面,我们只关心箱子的位置和人可以出现在箱子的上下左右哪些方向。我们对每个格子设出四个点,分别表示箱子在这个格子上,且人能够走到它的上、下、左、右四个方向的状态。那么假设一个人在箱子的左边,且箱子的右边是空地,那么这个状态就可以转移到右边的格子且人在左边的状态,建一条有向边,以此类推。
但是人在箱子的某个方向时,也可能可以通过路径走到箱子的另一个方向,例如从箱子的左边走到上面。于是对于每个箱子的位置,我们要找出箱子在这个位置上时哪些方向是可以互相到达的。由于箱子在某个格子上相当于删掉了这个格子,使其不连通,我们考虑新建一张图,使每个格子变为一个点,并将箱子的初始位置也看作空地,在相邻的空地之间连边。那么我们在这张图上面跑点双,如果某个格子对应的点是割点,那么意味着当箱子在这个格子上时,会有某些空地无法互相到达,此时相邻的格子中只有在同一个点双里的才能够互相到达。于是我们建出圆方树,当某个格子是割点时就将相邻的四个格子判断一下是否处在同个点双中,是的话在前面表示状态的图上连双向边,而不是割点的显然周围的格子都能互相到达,取一个点与其他所有点连双向边即可。显然每个点与外面连的边的数量是 \(O(1)\) 的,所以最终状态图的边数是 \(O(nm)\) 的。
最后在人的初始位置 BFS 一次,找到人刚开始时能在箱子的哪个方向,把其置为 \(1\),然后从那个状态开始 BFS 即可。最后询问时若格子的四个方向状态有任意一个为 \(1\),或者就是箱子的初始位置,那么这个格子可以被用箱子推到,否则不行。时间复杂度 \(O(nm)\)。
code:
#include <bits/stdc++.h>
#define in(x, y) ((x) >= 1 && (x) <= n && (y) >= 1 && (y) <= m)
#define tr(x, y) (((x) - 1) * m + (y))using namespace std;namespace Block {int cnt, head[4600000], to[10000000], nxt[10000000], dep[4600000], fa[4600000];void init() { memset(head, cnt = 0, sizeof(head)); }void add(int u, int v) {nxt[++cnt] = head[u];head[u] = cnt;to[cnt] = v;}void dfs(int g) {dep[g] = dep[fa[g]] + 1;for (int i = head[g]; i; i = nxt[i])if (to[i] ^ fa[g]) {fa[to[i]] = g;dfs(to[i]);}}bool eq(int x, int y) {if (dep[x] < dep[y])swap(x, y);if ((dep[y] ^ dep[x] - 2) && (dep[y] ^ dep[x]))return 0;else if (dep[y] == dep[x])return fa[x] == fa[y];elsereturn fa[fa[x]] == y;}
};namespace BFS {int tot, cnt, head[10000000], to[30000000], nxt[30000000];bool f[10000000];void init() { memset(head, tot = cnt = 0, sizeof(head)); }void add(int u, int v) {nxt[++cnt] = head[u];head[u] = cnt;to[cnt] = v;}void bfs(int s) {queue<int> q;int g;q.push(s);f[s] = 1;while (!q.empty()) {g = q.front();q.pop();for (int i = head[g]; i; i = nxt[i])if (!f[to[i]]) {q.push(to[i]);f[to[i]] = 1;}}}
};struct Node {int x, y;Node() { }Node(int _x, int _y): x(_x), y(_y) { }
};int n, m, q, ax, ay, bx, by, tot, scc, cnt, head[2300000], to[20000000], nxt[20000000], dfsn[2300000], low[2300000], st[2300000], ed, pos[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}}, p[4], dy[1505][1505][4];
char s[1505][1505];
bool key[2300000], bv[1505][1505];void add(int u, int v) {nxt[++cnt] = head[u];head[u] = cnt;to[cnt] = v;
}void tarjan(int g, int fa) {int ch = 0;dfsn[g] = low[g] = ++tot;st[++ed] = g;for (int i = head[g]; i; i = nxt[i])if (!dfsn[to[i]]) {++ch;tarjan(to[i], g);low[g] = min(low[g], low[to[i]]);if (low[to[i]] >= dfsn[g]) {if (fa) key[g] = 1;++scc;while (st[ed] ^ to[i]) {Block::add(st[ed], scc), Block::add(scc, st[ed]);--ed;}Block::add(st[ed], scc), Block::add(scc, st[ed]);Block::add(g, scc), Block::add(scc, g);--ed;}} else if (to[i] ^ fa)low[g] = min(low[g], dfsn[to[i]]);if (!fa && ch > 1)key[g] = 1;
}void bfs() {queue<Node> q;Node g;q.push(Node(ax, ay));bv[ax][ay] = 1;while (!q.empty()) {g = q.front();q.pop();for (int i = 0; i < 4; ++i)if (s[g.x + pos[i][0]][g.y + pos[i][1]] == '.' && !bv[g.x + pos[i][0]][g.y + pos[i][1]]) {q.push(Node(g.x + pos[i][0], g.y + pos[i][1]));bv[g.x + pos[i][0]][g.y + pos[i][1]] = 1;}}
}int main() {Block::init(), BFS::init();scanf("%d %d %d", &n, &m, &q);scc = n * m;for (int i = 1; i <= n; ++i)scanf("\r\n%s", s[i] + 1);for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j)if (s[i][j] ^ '#') {if (j < m && (s[i][j + 1] ^ '#'))add(tr(i, j), tr(i, j + 1)), add(tr(i, j + 1), tr(i, j));if (i < n && (s[i + 1][j] ^ '#'))add(tr(i, j), tr(i + 1, j)), add(tr(i + 1, j), tr(i, j));if (s[i][j] == 'A')ax = i, ay = j;else if (s[i][j] == 'B')bx = i, by = j;}for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j)if ((s[i][j] ^ '#') && !dfsn[tr(i, j)]) {tarjan(tr(i, j), ed = 0);Block::dfs(tr(i, j));}for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j)if (s[i][j] ^ '#')for (int k = 0; k < 4; ++k)if (in(i + pos[k][0], j + pos[k][1]) && (s[i + pos[k][0]][j + pos[k][1]] ^ '#'))dy[i][j][k] = ++BFS::tot;for (int i = 1; i <= n; ++i)for (int j = 1, c = 0; j <= m; ++j, c = 0)if (s[i][j] ^ '#') {for (int k = 0; k < 4; ++k) {if (in(i + pos[k][0], j + pos[k][1]) && (s[i + pos[k][0]][j + pos[k][1]] ^ '#'))p[++c] = k;if (in(i - pos[k][0], j - pos[k][1]) && (s[i - pos[k][0]][j - pos[k][1]] ^ '#'))BFS::add(dy[i][j][k], dy[i - pos[k][0]][j - pos[k][1]][k]);}if (c > 1)if (!key[tr(i, j)])for (int k = 1; k < c; ++k)BFS::add(dy[i][j][p[k]], dy[i][j][p[k + 1]]), BFS::add(dy[i][j][p[k + 1]], dy[i][j][p[k]]);elsefor (int k = 1; k < c; ++k)for (int l = k + 1; l <= c; ++l)if (Block::eq(tr(i + pos[p[k]][0], j + pos[p[k]][1]), tr(i + pos[p[l]][0], j + pos[p[l]][1]))) {BFS::add(dy[i][j][p[k]], dy[i][j][p[l]]), BFS::add(dy[i][j][p[l]], dy[i][j][p[k]]);break;}}bfs();for (int i = 0; i < 4; ++i)if (bv[bx + pos[i][0]][by + pos[i][1]]) {BFS::bfs(dy[bx][by][i]);break;}while (q--) {scanf("%d %d", &ax, &ay);if (ax == bx && ay == by)puts("YES");elsefor (int i = 0; i < 5; ++i)if (i == 4)puts("NO");else if (BFS::f[dy[ax][ay][i]]){ puts("YES"); break; }}return 0;
}