题解:P11681 [Algo Beat Contest 001 C] Creating a Queue
题目传送门
题目思路
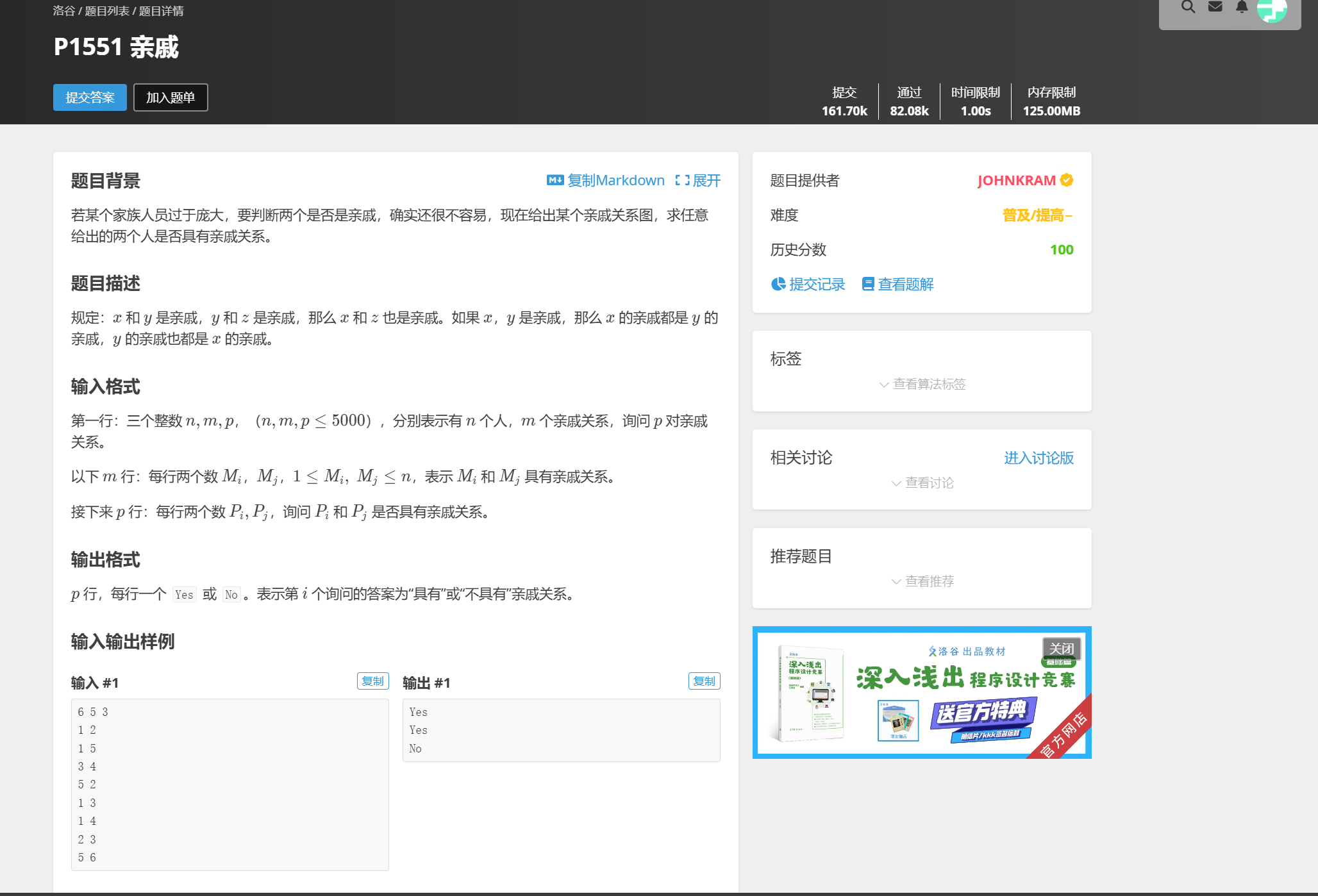
形式化题意
- 用 \(1\sim M\) 之间的正整数替换所有序列 \(A\) 中的 \(0\)。
- 构造出的序列不能有重复的元素。
- 证明:对于一个长度为 \(2\) 的序列,如果这个序列满足上述要求,那么这个序列的众数个数应当等于序列长度。因此,这个序列没有重复的元素。
- 当序列长度为 \(3\) 时,如果有两个元素相同,显然这就是一个不符合题意的最短的子串。
- 当序列长度为 \(4\) 时同理。也就是说对于一个序列,如果有一个元素(不包括 \(0\))的出现次数大度等于 \(2\),那么不符合题意的子串会随着元素出现次数的增多而增多。
- 证毕,推广开来,对于一个合法序列,这个序列中所有的非 \(0\) 元素一定不会重复出现。显然这个时候方案数为 \(0\)。
对应地,当一个序列满足形式化题意中所说的要求时,方案数如下:
- 首先要统计非 \(0\) 元素的个数,令个数为 \(n\)。因为不允许有重复的元素,所以原本的方案数 \(M\) 自然要减去 \(n\)。
- 对于第 \(i\) 个 \(0\),因为前面的 \(i-1\) 个 \(0\) 早就用完了 \(i-1\) 个方案数,因此方案数还要减去 \(i-1\)。
- 因此,对于 \(m\) 个 \(0\),\(n\) 个非 \(0\) 元素,答案为:\[\prod _{i=1}^{m} (M-n-(i-1))\bmod 1145141923=\prod _{i=1}^{m} (M-n-i+1)\bmod 1145141923 \]
代码实现
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD=1145141923;
const ll MAXN=1e6+10;
map<ll,ll>cnt;
ll n,m,a[MAXN],ans=1,sum=0,sum1=0;
int main(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>a[i];cnt[a[i]]++;if(cnt[a[i]]>1&&a[i]!=0){cout<<0;return 0;}}for(int i=1;i<=n;i++){if(a[i]!=0) sum++;else sum1++;} for(int i=1;i<=sum1;i++){ans=ans*(m-sum-(i-1))%MOD;}cout<<ans;
}