『做题记录』[CF1630D]Flipping Range

news/2025/2/8 22:59:34/文章来源:https://www.cnblogs.com/BlackCrow/p/18705570

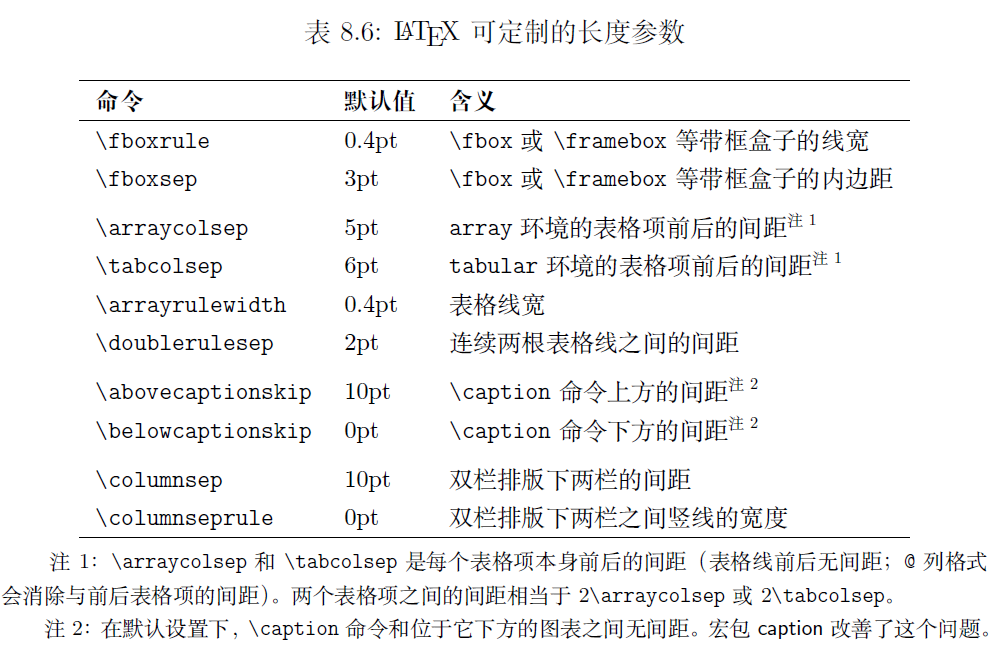
持续水（

[CF1630D]Flipping Range

Description

看luogu或者cf

Solution

这题属于是zak课件里“找不变量（特征量）”部分的板题，但zak讲课没说该怎么找（果然是做题型选手啊），于是只能自己琢磨了（

首先不难发现，给定的 \(b\) 数组其实可以先取 \(\gcd\) ，所有的可取反长度 \(b\) 可以拆分成它们的 \(\gcd\) 这点应该是比较显然的。那么接下来操作实际上变为了可以对长度为 \(L=\gcd_i(b_i)\) 的区间取反。

区间是很难处理的，我们不希望处理区间，于是我们就可以 异或差分 ，通过考虑连续操作两次来将距离为 \(L\) 的两个数取反。到这里就很明显了，我们将所有的数按 \(\bmod L\) 的余数分类依次处理，每次我们可以取反相邻两个数。当负数个数为偶数时，我们是可以把它们全部变成正数的；奇数时，我们则必须留下一个负数，选最大的那个即可。

需要注意的是，我们可以通过在一开始对 \([1,L]\) 进行一次操作来使负数奇偶性反转，这里计算这种情况下的答案，两种情况取 \(\min\) 即可。

Code

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
#define mp make_pair
#define vi vector<int>
#define eb emplace_back
#define pii pair<int, int>
#define fi first
#define se second
#define Rep(rp,a,b) for(int rp=a;rp<b;++rp)
#define rep(rp,a,b) for(int rp=a;rp<=b;++rp)
#define per(bl,a,b) for(int bl=a;bl>=b;--bl)
mt19937 rnd(114514);
#define segc int mid = L+R>>1, lc = now<<1, rc = lc|1
const int N = 1e6+5, MOD = 998244353, INF = 1e9;
template <typename T> inline void chkmin(T &x,T y) {x = y>x ? x : y;}
template <typename T> inline void chkmax(T &x,T y) {x = y>x ? y : x;}
inline int read() {register int x = 0, f = 1;register char ch = 0;while(ch < 48 || ch > 57) {ch = getchar();if (ch == '-') f = -1;}while(ch >= 48 && ch <= 57) x = x*10+(ch^48), ch = getchar();return f*x;
}int a[N];void solve() {int n = read(), m = read(), gc, b;LL ans = 0;Rep (i, 0, n) a[i] = read(), ans += abs(a[i]);rep (i, 1, m) b = read(), gc = (i==1)?b:__gcd(gc, b);if (gc == 1) return (void)printf("%lld\n", ans);LL ans1 = ans, ans2 = ans;Rep (i, 0, gc) {int cntn = 0, mn = INF;rep (j, 0, (n-i-1)/gc) cntn += (a[j*gc+i] < 0), chkmin(mn, abs(a[j*gc+i]));if (cntn&1) ans1 -= 2*mn;else ans2 -= 2*mn;}printf("%lld\n", max(ans1, ans2));
}int main() {int T = read(); while (T --) solve();return 0;
}