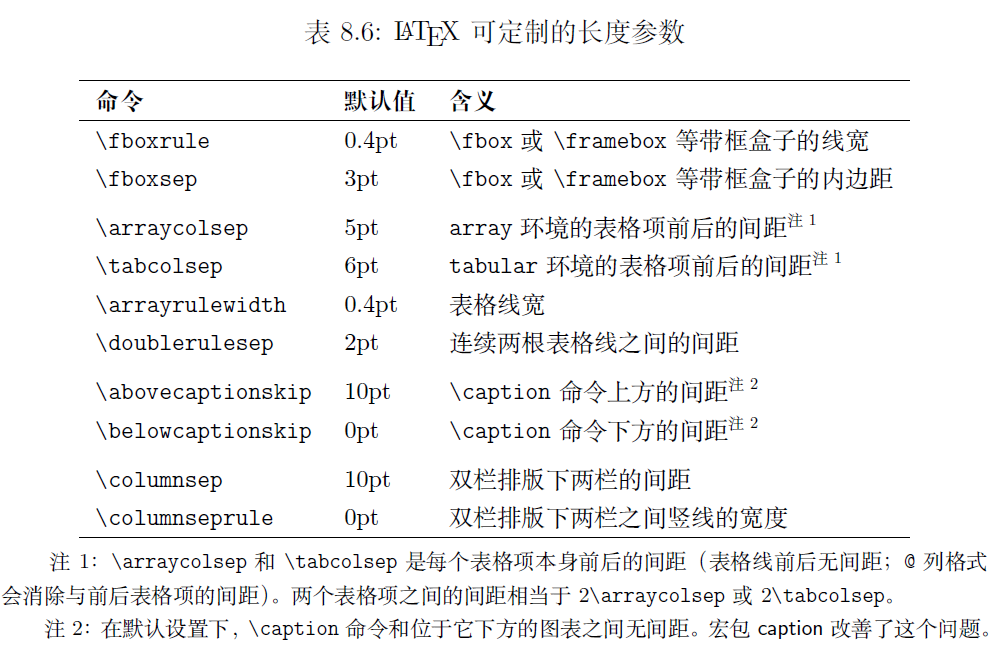
A - Shuffled Equation
显然只有最大值可能被相乘得到,所以对\(a\)从小到大排序,判断\(a[0]\times a[1]=a[2]\)是否成立即可。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int a[3];
signed main(){cin>>a[0]>>a[1]>>a[2];sort(a,a+3);cout<<(a[0]*a[1]==a[2]?"Yes\n":"No\n");return 0;
}
B - Who is Missing?
用桶记录每个数的选取情况,枚举\(1\sim n\)所有数,输出所有未被选择的数即可。
点击查看代码
#include<bits/stdc++.h>
#define N 1010
using namespace std;
int n,m,cnt;
bitset<N> vis;
signed main(){cin>>n>>m;for(int i=1,a;i<=m;i++) cin>>a,vis[a]=1;for(int i=1;i<=n;i++) if(!vis[i]) cnt++;cout<<cnt<<"\n";for(int i=1;i<=n;i++) if(!vis[i]) cout<<i<<" ";return 0;
}
C - Bib
题目是让我们对于每个\(i\),求穿\(i\)号围兜的人盯着的人穿几号围兜。
用\(b[i]\)表示穿\(i\)号围兜的人,我们在输入的过程中处理出来。则根据上面的分析,第\(i\)个答案为\(q[p[b[i]]]\)。
点击查看代码
#include<bits/stdc++.h>
#define N 300010
using namespace std;
int n,p[N],q[N],b[N];
signed main(){cin>>n;for(int i=1;i<=n;i++) cin>>p[i];for(int i=1;i<=n;i++) cin>>q[i],b[q[i]]=i;for(int i=1;i<=n;i++) cout<<q[p[b[i]]]<<" ";return 0;
}
D - Doubles
暴力枚举是\(O(n^2 V)\)的,其中\(V=10^5\)表示值域。考虑优化。
实际上对于我们枚举的\((i,j)\)这对骰子,仅需枚举其中一个骰子可能的点数即可,并不需要把\(1\sim 10^5\)的点数都枚举一遍。
分析一下时间复杂度:\(O(\sum\limits_{i,j}k[i])=O(\sum\limits_j S)=O(nS)\),其中\(S=\sum k=10^5\)。
点击查看代码
#include<bits/stdc++.h>
#define N 105
#define S 100010
using namespace std;
int n;
unordered_set<int> se[N];
double p[N][S],maxx;
signed main(){cin>>n;for(int i=1,m,x;i<=n;i++){cin>>m;double tmp=1.0/m;for(int j=1;j<=m;j++)cin>>x,p[i][x]+=tmp,se[i].insert(x);}for(int i=1;i<n;i++){for(int j=i+1;j<=n;j++){double ans=0;for(int k:se[i])ans+=p[i][k]*p[j][k];maxx=max(maxx,ans);}}cout<<fixed<<setprecision(18)<<maxx;return 0;
}
悄悄告诉你:由于此题玄学的数据,\(O(n^2 S)\)的暴力也可以过(Link)。
E - Cables and Servers
容易发现,最优操作下,每操作一次连通块就减少\(1\)。所以最少操作次数就是整张图的连通块个数\(-1\)。
再考虑如何输出方案。显然最优操作下,每个操作都必须合并\(2\)个连通块。换句话说,不能因为我们动用某条边,就使得原来的一整个连通块断成两半。
所以我们不妨规定,只动用原图生成树之外的边。
这样做法就出来了,我们对原图跑生成树,遍历生成树外的边,每条边选取其中一个端点,连向其他连通块中的任意一个即可。
点击查看代码
#include<bits/stdc++.h>
#define N 200010
#define M 200010
using namespace std;
int n,m,fa[N],to[M];
struct edge{int to,num;};
bitset<M> flg;
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
unordered_set<int> se;
signed main(){cin>>n>>m;for(int i=1;i<=n;i++) fa[i]=i;for(int i=1,u,v;i<=m;i++){cin>>u>>v,to[i]=u;//to[i]=v;也可以u=find(u),v=find(v);if(u==v) continue;fa[u]=v,flg[i]=1;}for(int i=1;i<=n;i++) se.insert(find(i));cout<<se.size()-1<<"\n";for(int i=1;i<=m;i++){if(se.size()==1) break;if(flg[i]) continue;auto it=se.begin();if((*it)==find(to[i])) it++;//避免自己连向自己fa[*it]=find(to[i]);cout<<i<<" "<<to[i]<<" "<<(*it)<<"\n";se.erase(it);}return 0;
}
F - Insert
看到题面首先想到平衡树之类的结构来模拟,又不想实现平衡树了,就想到用rope来维护序列,算了一下时间在\(3\times 10^8\)左右,交上去搏一把,很不幸\(\tt TLE\times 4\)(Link)。
(rope是pb_ds库的一个分支,底层实现是块状链表,可以支持\(O(\sqrt n)\)的插入、删除等操作,从c++11开始受支持,具体用法可以自行搜索)
[To Be Continued]
电脑没电了,明天更新正解。