dp 大典

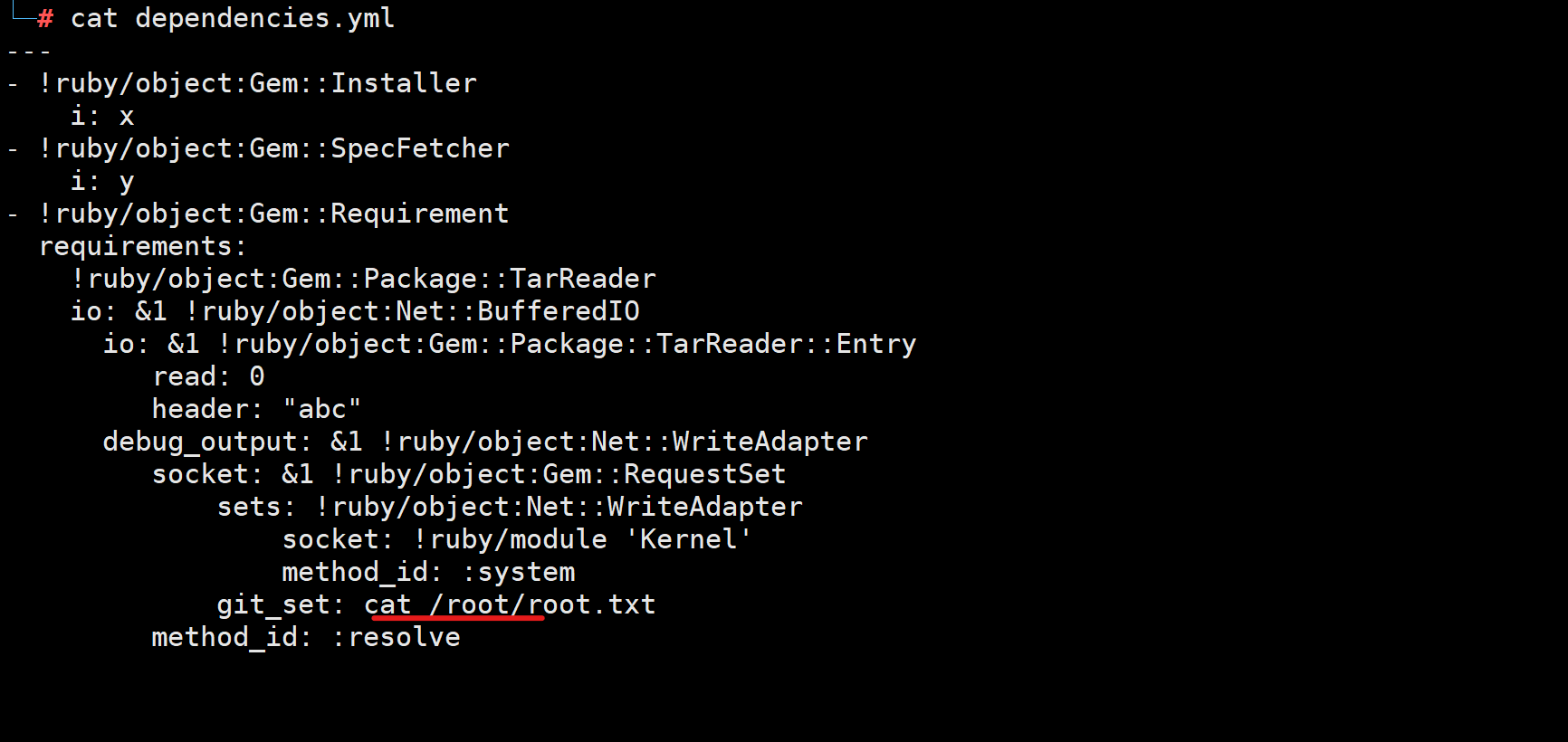
作为 OI 里面分支最多的模块之一，dp 在 OI 中有着重要的作用，现在，让我们一起走进 dp 的世界：

注：我在每道题前面都标注了个人难度，范围大概是 \([1,50]\) 吧（

AT_dp 系列

众所周知，Atcoder 中有一套全是 dp 的题目，难度大致逐渐增加，我们可以从中学到很多 dp 的知识。

AT_dp_a ~ AT_dp_c

个人难度：\(3\)。

这部分非常的简单，初学 dp 的人也不难做出来。

AT_dp_d（背包）

个人难度：\(4\)。

背包问题的板子：

for(int i=1;i<=n;++i){for(int j=m;j>=w[i];--j){dp[j]=max(dp[j],dp[j-w[i]]+v[i]);}}

我们发现本题为 \(01\) 背包，所以第二层循环要倒着枚举。如果是完全背包则要正着枚举。

AT_dp_e

个人难度：\(6\)。

和上一题题面完全一样，但背包容量最大能到 \(10^9\)，这该怎么办呢？

注意到 \(v_i\le 10^3\)，所以可以考虑转换状态，即设 \(dp_{i,j}\) 表示到了第 \(i\) 个物品，价值总和为 \(j\) 时，重量最小为多少，转移也很简单：

for(int i=1;i<=n;++i){for(int j=1e5;j>=v[i];--j){dp[j]=min(dp[j],dp[j-v[i]]+w[i]);}}

最后找到 \(dp_{n,i}\le m\) 的最大 \(i\) 即可。这个算法的时间复杂度为 \(O(n^2v_i)\)。

AT_dp_f（LCS）

个人难度：\(8\)。

LCS 板子，dp 部分很简单：

for(int i=1;i<=n;++i){for(int j=1;j<=m;++j){if(s[i]==t[j])dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}

但是此题还要输出方案，这是本题的难点。不过没关系，我们只需要从最后一步开始，倒着进行 dp 的过程，寻找上一次从哪转移来的即可。

while(dp[x][y]){if(s[x]==t[y])ans[dp[x][y]]=s[x],--x,--y;else{if(dp[x][y]==dp[x-1][y])--x;else --y;}}

AT_dp_g

个人难度：\(5\)。

这道题很简单，求有向无环图最长路，其实里面也蕴含了一个技巧，就是 DAG 上的 dp。对于这种 dp，我们可以在拓扑排序过程中进行 dp：

while(!q.empty()){int u=q.front();q.pop();for(int v:e[u]){dp[v]=max(dp[v],dp[u]+1);--in[v];if(!in[v])q.push(v);}}

AT_dp_h

个人难度：\(3\)。

和过河卒是一样的，挺简单的。

AT_dp_i（概率 dp）

个人难度：\(11\)。

难度从这一刻起来了。

这是一道概率 dp，但是还不算太难。遇到这种正面反面的问题，可以考虑设 \(dp_{i,j}\) 表示前 \(i\) 个里面有 \(j\) 个是向上的，则有转移方程 \(dp_{i,j}=dp_{i-1,j-1}p_i+dp_{i-1,j}(1-p_i)\)。

对于这个题，统计答案只需要枚举向上的硬币数量，累加 dp 值即可。

AT_dp_j

个人难度：\(18\)。

这个题也是概率 dp，但比上一个难很多。

首先对于随机选盘子而言，盘子的顺序对期望值没有影响。这一点对于本题是很重要的。

因为 \(1\le a_i \le 3\)，所以可以把寿司的四种可能值 \(0,1,2,3\) 都设在 dp 转移方程里（即一个四维状态），进行转移。

但是这样状态是 \(n^4\) 的，过不去。注意到 \(0,1,2,3\) 的个数只需要知道三个就可以反推剩下一个，所以可以只保留三维状态。

for(int k=0;k<=n;++k){for(int j=0;j<=n;++j){for(int i=0;i<=n;++i){if(i||j||k){if(i)dp[i][j][k]+=dp[i-1][j][k]*i/(i+j+k);if(j)dp[i][j][k]+=dp[i+1][j-1][k]*j/(i+j+k);if(k)dp[i][j][k]+=dp[i][j+1][k-1]*k/(i+j+k);dp[i][j][k]+=(double)n/(i+j+k);}}}}

AT_dp_k（博弈 dp）

个人难度：\(6\)。

这算是一个很初级的博弈 dp，因为状态和转移都很简单。

考虑设 \(dp_i\) 表示当石子个数为 \(i\) 时先手能否获胜，则如果它前面能转移到它的 dp 值有一个为 \(0\)，则 \(dp_i=1\)（因为两人是按最优策略走的）。

for(int i=1;i<=k;++i){for(int j=1;j<=n;++j){if(a[j]<=i&&!dp[i-a[j]])dp[i]=1;}
}

AT_dp_l（区间 dp）

个人难度：\(8\)。

这种双端队列两人取数，肯定最先想到区间 dp。于是可以设 \(dp_{l,r}\) 为 \([l,r]\) 区间的答案，则很容易做到 \(O(n^2)\) 转移。

这个区间 dp 和平常我们做的（如石子合并）还是有一些不同的，因为它不用枚举区间端点。

当然本题有 \(O(n)\) 解法，即我们把所有的“峰”都合并：若 \(a_{i-1},a_{i+1}\le a_i\)，则把它们合并为一个新的元素 \(a_{i-1}+a_{i+1}-a_i\)。重复以上操作，直至没有“峰”。此时贪心就是对的，但是这个合并的操作的正确性不会证明。

AT_dp_m（前缀和优化 dp）

个人难度：\(10\)。

这种问题通常涉及到前面一些连续 dp 状态的和，这时我们可以用前缀和来优化转移。大体是这样的：

for(int i=1;i<=n;++i){for(int j=0;j<=k;++j){dp[i][j]=(f[j]-(j-a[i]-1>=0?f[j-a[i]-1]:0)+mod)%mod;}f[0]=dp[i][0];for(int j=1;j<=k;++j)f[j]=(f[j-1]+dp[i][j])%mod;}

也是非常的好理解。

AT_dp_n

个人难度：\(9\)。

这就是我们常说的石子合并问题了，同样用区间 dp 解决，转移方程也是非常直接：

dp[l][r]=min(dp[l][r],dp[l][i-1]+dp[i][r]+sum[r]-sum[l-1]);

其中 \(sum\) 是前缀和数组，\(i\) 是枚举的断点。

AT_dp_o（状压 dp）

个人难度：\(20\)。

从这里开始难度又上升了一个档次。

求二分图完全匹配数量？看上去是一个很经典的问题，但是普通的 dp 状态难以解决这个问题。注意到 \(n\le 21\)，所以我们可以直接用二进制表示一个集合，把集合放到状态里。

大家都知道，二分图是有两部分点的，鉴于时空都有限，我们只能表示出一个集合。所以我们设 \(dp_{i,j}\) 表示左部前 \(i\) 个点和右部集合 \(j\) 的匹配数量。

转移的时候，枚举刚才说的 \(i,j\)，然后再枚举一个不在右部且与 \(i\) 能匹配的右部点 \(k\)，主动更新下一个状态：

dp[0][0]=1;for(int i=1;i<=n;++i){for(int j=0;j<(1<<n);++j){if(__builtin_popcount(j)!=i-1)continue;for(int k=1;k<=n;++k){if(a[i][k]&&!((1<<k-1)&j))dp[i][j|(1<<k-1)]=(dp[i][j|(1<<k-1)]+dp[i-1][j])%mod; }}}

时间复杂度 \(O(2^nn^2)\)。

AT_dp_p（树形 dp）

个人难度：\(8\)。

这是一道比较简单的树形 dp。

对于这种涂黑涂白的问题，可以设 \(dp_{i,0}\) 表示 \(i\) 涂白时以 \(i\) 为根节点的子树内的方案数，\(dp_{i,1}\) 则是黑色的情况，然后在 dfs 的过程中转移即可：

void dfs(int u,int fa){dp[u][0]=dp[u][1]=1;for(int v:e[u]){if(v==fa)continue;dfs(v,u);dp[u][0]=dp[u][0]*(dp[v][0]+dp[v][1])%mod;dp[u][1]=dp[u][1]*dp[v][0]%mod;}
}

AT_dp_q（数据结构优化 dp）

个人难度：\(10\)。

带权 LIS，十分经典的问题。

在 \(n^2\) 解法中，我们的转移方程是 \(f_i=\min\{f_j,j<i\wedge h_j<h_i\}+a_i\)。但是这个转移方程的状态只有 \(n\)，说明我们有可能能优化转移。

我们如果从前往后更新 \(f_i\)，那么 \(j<i\) 就代表前面所有的 \(j\)。还有一个限制是 \(h_j<h_i\)，这个就是我们要处理的。

这时我们相当于要维护一个集合，支持加入数，查询 \(h\) 值小于某个数的 \(f\) 值最小值。考虑把 \(h\) 放在下标，这时相当于维护序列，支持单点修改，前缀最小值，直接采用树状数组进行优化。至此，我们得到了 \(O(n \log n )\) 的代码。

struct BIT{int c[N];void add(int x,int k){while(x<=n){c[x]=max(c[x],k);x+=x&-x;}}int ask(int x){int ans=0;while(x){ans=max(ans,c[x]);x-=x&-x;}return ans;}
}A;
signed main(){cin>>n;for(int i=1;i<=n;++i)cin>>h[i];for(int i=1;i<=n;++i)cin>>a[i];for(int i=1;i<=n;++i){dp[i]=A.ask(h[i]-1)+a[i];A.add(h[i],dp[i]);ans=max(ans,dp[i]);}cout<<ans;return 0;
} 

其实还是挺好写的，熟悉了之后 \(5\) 分钟就能写出来。

AT_dp_r（矩阵快速幂优化 dp）

个人难度：\(11\)。

求长度为 \(k\) 的路径条数？

我们可以设 \(f_{k,i,j}\) 表示 \(i\sim j\) 的长度为 \(k\) 的路径条数，那么可以得到转移方程：

\(f_{k,i,j}=\sum\limits_{l=1}^n f_{k-1,i,l}\times f_{1,l,j}\)

这和矩阵乘法完全一样，所以直接对邻接矩阵矩阵快速幂即可。

AT_dp_s（数位 dp）

个人难度：\(17\)。

这种求 \(1\sim k\) 满足某种条件的数的个数且 \(k\) 很大的题，大概率是数位 dp。

注意到 \(d\) 很小，所以设可以用 \(dp_{i,j}\) 表示当前填到第 \(i\) 位，数位和模 \(d\) 位 \(j\) 的答案。注意，这个“答案”必须是在前面数位没有限制的情况取，不然不同的情况可能会有不同的答案，直接调用会引发错误。

实现方式通常采用记忆化搜索的方式，从高位往低位填数：

int dfs(int eq,int dep,int sum){if(!dep)return (sum==0);if(!eq&&f[dep][sum]!=-1)return f[dep][sum];int en=(eq?a[dep]:9),ans=0;for(int i=0;i<=en;++i)ans=(ans+dfs(eq&&(i==en),dep-1,(sum+i)%d))%mod;if(!eq)f[dep][sum]=ans;return ans;
}

AT_dp_t

个人难度：\(23\)。

我们已经来到了本套题最难的几道题目。

排列计数问题，我们发现排列具体是什么我们不关心，只需要知道相对大小顺序即可。

于是设 \(dp_{i,j}\) 表示填到第 \(i\) 个位置，且 \(i\) 元素在 \(1\sim i\) 组成的序列中为第 \(j\) 小（这状态似乎是这些题里最不好想的一个）。然后分两种情况：

• 字符为 \(<\)，此时上一个位置的排名必须比 \(j\) 小，即 \(dp_{i,j}=\sum\limits_{k=1}^{j-1}dp_{i-1,k}\)。

• 字符为 \(>\)，此时上一个位置的排名必须大于等于 \(j\)，即 \(dp_{i,j}=\sum\limits_{k=j}^{i-1}dp_{i-1,k}\)。

  为什么会有等于？因为 \(i\) 的排名比 \(i-1\) 小，所以原本排名为 \(j\) 的会变成 \(j+1\)，故可以取到等于。

观察两个方程，发现可以前缀和优化到 \(O(n^2)\)，这样就可以通过了。

AT_dp_u

个人难度：\(21\)。

哦，\(n\le 16\)，又是我们熟悉的状压 dp。

注意到我们甚至可以把每个子集的贡献都预处理出来（设为 \(V\)），这部分时间复杂度是 \(O(2^nn^2)\)。

然后设 \(dp_{i}\) 表示 \(i\) 这个状态下的得分最大值，我们可以得到转移方程：

\(dp_i=max\{dp_j+V_{i\oplus j},j\in i\}\)

这个也很好理解，我们只需要把这部分分成某个子集和其余部分，然后取最大值就可以了。

问题就是，后面这部分时间复杂度是 \(O(4^n)\)，大概率是过不去的。

但是真的是这样吗？注意到，我们如果不重不漏地枚举子集，那么其实时间复杂度是：

\[\sum_{i=0}^nC_n^i\times 2^i=3^n \]

也就是说，我们只需要一种能不重不漏枚举子集的方法就好了！

这种方法当然是存在的，它就在这里：

for(int j=i;j;j=(j-1)&i){//j 是 i 的子集
}

所以按照刚才的方法 dp 即可。

AT_dp_v（换根 dp）

个人难度：\(19\)。

这个染出来的连通块是无根树，所以树形 dp 状态就很难设了。

所以考虑先设 \(dp1_u\) 为以 \(u\) 为根的子树内，必选 \(u\) 组成的连通块的方案数，那么有：

\[dp1_u=\prod_v (dp1_v+1) \]

这是很好理解的，因为每个子节点 \(v\) 选的话有 \(dp1_v\) 种可能，不选的话有 \(1\) 种可能。

然后再设 \(dp2_u\) 为以 \(u\) 为根的子树外，必选 \(u\) 组成的连通块的方案数，那么有：

\[dp2_u=(dp2_{fa}\times \prod_k (dp1_k+1))+1 \]

其中 \(k\) 是 \(u\) 所有的兄弟，\(fa\) 是 \(u\) 的父节点。这个也不难理解，\(u\)“外面的节点”无非就是 \(fa\)“外面的节点”和 \(u\) 自己的兄弟两部分构成。最后那个 \(+1\) 别忘了，单独一个点也是答案。

然后根据乘法原理，\(dp1_u\times dp2_u\) 就是答案了。整个过程可以用前、后缀和优化到 \(O(n)\)。

void dfs1(int u,int fa){dp1[u]=1;vector<int>son;for(int v:e[u]){if(v==fa)continue;dfs1(v,u);dp1[u]=dp1[u]*(dp1[v]+1)%mod;son.push_back(v);}int pr=1;for(int i=0;i<son.size();++i){pre[son[i]]=pr;pr=pr*(1+dp1[son[i]])%mod;}pr=1;for(int i=son.size()-1;i>=0;--i){suf[son[i]]=pr;pr=pr*(1+dp1[son[i]])%mod;}
}
void dfs2(int u,int fa){if(!fa)dp2[u]=1;else dp2[u]=(dp2[fa]*pre[u]%mod*suf[u]%mod+1)%mod;for(int v:e[u]){if(v!=fa)dfs2(v,u);}
}

AT_dp_w

个人难度：\(?\)。

我也不知道这线段树优化 dp 我为啥看不懂，等我看懂了再写。

AT_dp_x（贪心优化 dp）

个人难度：\(23\)。

对于这种问题，可以拎出来两个位置 \(i,j\) 进行讨论，讨论出来它们的关系，我们就知道了整体的偏序关系。这个方法叫 Exchange arguments。

如果 \(i\) 在下 \(j\) 在上，我们还能往上堆 \(s_i-w_j\) 的重量，否则能堆 \(s_j-w_i\) 的重量，所以把 \(i\) 放在下面当且仅当 \(s_i-w_j>s_j-w_i\)，即 \(w_i+s_i>w_j+s_j\)。

所以按照 \(w_i+s_i\) 排序跑 \(01\) 背包即可，时间复杂度 \(O(nS)\)。

AT_dp_y（dp+排列组合）

个人难度：\(22\)。

神秘的状态设计方式……

设 \(dp_i\) 表示当前到了第 \(i\) 个障碍，不经过前面的任何一个障碍的方案数。则有转移：

\[dp_i=C_{x_i+y_i-2}^{x_i-1}-\sum\limits_{j=1}^{i-1}C_{x_i-x_j+y_i-y_j}^{x_i-x_j}dp_j \]

其中 \(C_{x_i+y_i-2}^{x_i-1}\) 是当没有障碍时，\((1,1)\) 到 \((x_i,y_i)\) 的方案数。把之前所有经过障碍的方式全减掉。因为这个方案是记录的“不经过任何障碍”，所以不会出现重复的情况。

为了好写可以把终点当作第 \((n+1)\) 个障碍。

AT_dp_z（斜率优化 dp）

个人难度：\(32\)。

boss 题来了！

显而易见得到 \(n^2\) 转移：

\[dp_i=\min\{dp_j+(h_i-h_j)^2+C,j<i\} \]

然后可以化简 \(\min\) 里面的：

\[dp_j+{h_i}^2+{h_j}^2-2h_ih_j+C \]

我们可以把与 \(j\) 无关的项取出，这样还剩下：

\[{h_j}^2+dp_j-2h_ih_j \]

设 \(f(j)={h_j}^2+dp_j\)，\(k=-2h_i\)，则原式变成：

\[f(j)+kh_j \]

再用 Exchange arguments 的技巧，若 \(j1<j2\)，且 \(j1\) 优于 \(j2\)，则有：

\[f(j1)+kh_{j1}\le f(j2)+kh_{j2} \]

整理得：

\[k\le \frac{f(j2)-f(j1)}{h_{j2}-h_{j1}} \]

哎这不是我们斜率的式子吗？

所以设 \(s(a,b)=\frac{f(a)-f(b)}{h_a-h_b}\)，此时若有三个点 \(a,b,c\)（\(a<b<c\)），如果 \(b\) 是最优决策点，此时应满足 \(s(a,b)\le k\) 且 \(s(b,c)\ge k\)，即 \(s(a,b)\le s(b,c)\)。

所以我们维护一个下凸壳就可以解决这个问题了！

对于下凸壳的维护，我们可以采用单调队列，具体来说步骤如下：

• 若前两个元素不满足前一个元素更优，将前一个元素出队。

• 此时头元素为最优转移点，转移 \(dp_i\)。

• 把队尾不优于 \(i\) 的出队。

• 把 \(i\) 入队。

#include<bits/stdc++.h>
#define int long long
#define N 1000005
using namespace std;
int n,c,h[N],l,r,q[N],dp[N];
double Y(int i){return dp[i]+h[i]*h[i];
}
double X(int i){return h[i];
}
double slope(int i,int j){return (Y(j)-Y(i))/(X(j)-X(i));
}
signed main(){cin>>n>>c;for(int i=1;i<=n;++i)cin>>h[i];l=r=q[1]=1;for(int i=2;i<=n;++i){while(l<r&&slope(q[l],q[l+1])<=h[i]*2)++l;int j=q[l];dp[i]=dp[j]+(h[i]-h[j])*(h[i]-h[j])+c;while(l<r&&slope(q[r-1],q[r])>=slope(q[r],i))--r;q[++r]=i;}cout<<dp[n];return 0;
}

AT_tdpc 系列

好的我们成功的来到了下一个系列，做好准备了吗？让我们更深一步走进 dp！

（那些紫题有点难，先咕一会）

---

别的 DP 技巧

这里是一些别的 dp 技巧，可能有很多是打 ABC 时我没做出来的题。

AT_abc385_g（多项式优化 dp）

个人难度：\(39\)。

首先先想不算很难的 \(n^2\) dp，设 \(f_{i,j}\) 表示 \(n-i+1 \sim n\) 的数组成的序列 \(p\) 中，\(L(p)-R(p)=j\) 的 \(p\) 的个数。

转移比状态简单：\(f_{i,j}=f_{i-1,j-1}+f_{i-1,j+1}+f_{i-1,j}(i-2)\)。

这个时候就要观察了，发现转移用到的全是 \(i-1\) 那行的 dp 值，所以可以把它变成一个多项式，那么 \(j-1\) 到 \(j\) 就是右移，\(j+1\) 到 \(j\) 就是左移。所以有：

\(f_1=1\)；

\(f_i=(x+x^{-1}+(i-2))f_{i-1}\)

然后化整式后 NTT 即可。

AT_abc386_f（去除 dp 无用状态）

个人难度：\(17\)。

哎这不是我们编辑距离问题吗，等等为啥是 \(5\times 10^5\)？

哦原来是判定性问题，而且 \(k\le 20\) 是切入点。但是状压什么的显然不行。

想想我们编辑距离问题里设的状态，\(dp_{i,j}\) 是 \(S\) 前 \(i\) 个和 \(T\) 前 \(j\) 个的编辑距离，这个状态似乎有些特别。因为当 \(|i-j|> k\) 的时候，这个值一定大于 \(k\)，又因为 dp 数组在转移的过程中转移过后的状态比之前的要大，所以此时 \(dp_{i,j}\) 不可能对答案造成贡献。

然后这时只有 \(nk\) 个状态，这样我们就过了。

AT_abc389_g（巨大计数 dp）

个人难度：\(32\)。

这不太像人类能出出来的题：求满足与 \(1\) 的最短路长度为奇数和偶数的点的数量相等的 \(n\) 个点的图的个数。

然后我们发现：\(n\le 30\)。

这下可做了，但是注意到 \(n\) 是 \(30\) 而不是 \(20\) 之类的，说明状压大概不可行。折半搜索什么的就别想了，显然做不了。

这下大概只有一种可能了，就是正解的时间复杂度可能是 \(O(n^k)\)，这题看上去 \(k\) 是大概 \(5,6\) 的一个数（只是看上去）。

这种计数题必须把状态设全，才能保证转移的过程中能转。首先这题一个很重要的性质是，这个满足条件的图大概是这样的：

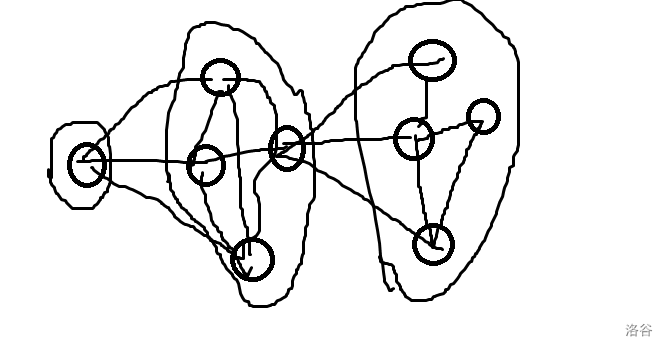
我们发现图按照到一号点的最短路距离进行了分层，且有以下性质：

• \(1\) 号点在第一层，且第一层只有 \(1\) 号点。

• \(i\)（\(i>1\)）层的任意点必须和 \(i-1\) 层中的至少一个点连边。

• 层内随意连边。

• 只有相邻的层有边相连。

• 奇数层和偶数层总点数相等（这图没体现这点，因为是我乱画的）。

然后我们看看 dp 需要什么：

• 现在是第几层。

• 这层有多少点。

• 一共有多少点，多少边。

• 奇数层有多少点、偶数层有多少点。

你可能会问为什么不需要知道这层有多少边，这个等会转移的时候我们就知道了。

现在开始设状态。注意到知道了“奇数层有多少点、偶数层有多少点”，也就知道了一共有多少点。而且“现在是第几层”其实不重要，只需要记录该层的奇偶性（当然只是减少了空间）。所以设 \(f_{i,j,k,l,s}\) 表示当前深度奇偶性为 \(i\)，连了 \(j\) 条边，奇数层有 \(k\) 个，偶数层有 \(l\) 个，当前层有 \(s\) 个点的答案。

接下来是转移。我们发现 \(i-1\) 层到 \(i\) 层只需要知道加了多少个点（\(x\)）、多少条边（\(y\)）。所以我们得到了：

\[f_{1,j+y,k,l+x,x}=f_{1,j+y,k,l+x,x}+f_{0,j,k,l,x}C_{n-k-l}^xg_{s,x,y} \]

其中 \(g_{s,x,y}\) 是一个要算很多次的贡献，即 \(s\) 个点连出 \(y\) 条边使得 \(x\) 个点每个都至少与 \(s\) 个点中的一个相连的方案数。这个东西在这里算显然不划算，所以可以预处理出来（等会再说怎么预处理）。这个组合数 \(C_{n-k-l}^x\) 就是在剩余的点里取 \(x\) 个，也不是很难理解。当然同理有：

\[f_{0,j+y,k,l+x,x}=f_{0,j+y,k,l+x,x}+f_{1,j,k,l,x}C_{n-k-l}^xg_{s,x,y} \]

这个时候我们就发现了，没有当前层的边数照样也能转移，所以根本不需要记录。

然后是 \(g_{i,j,k}\)，在 \(j-1\) 个点到 \(j\) 个点的过程中，我们可以枚举这个点连了多少条边，那么就得到了：

\[g_{i,j,k}=\sum_{l=1}^{\min(i+j-1,k)}(C_{i+j-1}^l-C_{j-1}^l)g_{i,j-1,k-l} \]

这个 \(C_{i+j-1}^l-C_{j-1}^l\) 是怎么来的？其实是因为不算新来的点两层一共有 \(i+j-1\) 个点，所以可以随便连 \(l\) 个。但是必须和那 \(i\) 个点有连边，所以减去全都连到 \(j-1\) 个点的情况。

分析一下复杂度，瓶颈在 \(f\) 的转移，是 \(O(n \cdot n^2 \cdot n \cdot n \cdot n^3)=O(n^8)\) 的。但是我们发现我们自带极小的常数，再加上有一些状态是 \(0\) 可以直接跳过转移，我们就可以通过这道题目了。

AT_abc391_g（dp 套 dp）

个人难度：\(24\)。

我们想一下我们平时是怎么做 LCS 的，设 \(dp_{i,j}\) 表示 \(s\) 的前 \(i\) 个字符与 \(t\) 的前 \(j\) 个字符的 LCS，则有：

• 若 \(s_i=t_j\)，\(dp_{i,j}=dp_{i-1,j-1}+1\)。

• 否则，\(dp_{i,j}=\max(dp_{i-1,j},dp_{i,j-1})\)。

现在要求满足条件的 \(t\) 的个数了，我们可以设 \(dp_{i,s_2}\) 表示满足 \(t\) 的前 \(i\) 个字符与 \(s\) 的 LCS 是 \(s_2\) 的 \(t\) 的个数，然后转移的时候枚举下一位是什么就可以。

那么问题来了，这个东西的状态看起来很多，我们应该如何优化？

事实上，我们可以先把 \(s_2\) 换成我们开头那个 dp 数组中的一行，因为我们知道这一行就知道了下一行的状态。接下来，因为每增加一位 LCS 最多增加 \(1\)，所以我们最开头说的那个 dp 数组的相邻两行的差分只可能是 \(0\) 或 \(1\)（所以再用差分数组代替 dp 数组）。然后我们需要做的就是：

• 先预处理出来每个差分数组后面添加每个字符会变成的差分数组。

• 转移时枚举后面是哪一位，更新 dp 状态。

这两部分都可以采用状压处理，总时间复杂度为 \(O(2^nm(n+\alpha))\)，其中 \(\alpha\) 为字母表大小 \(26\)。