什么是SFM?
SFM(Structure from Motion)即运动结构恢复,通过给出多幅图像及其图像特征的一个稀疏对应集合,从而估计3D点的位置,这个求解过程通常涉及3D几何(结构)和摄像机姿态(运动)的同时估计。

如何求解相关参数?
从图中可以得出,我们需要求解的主要内容有两个,一个是运动矩阵 \(M\),即相机的姿态;另一个是结构矩阵 \(X\),即3D点的真实位置。
首先我们思考一下,如果我们已知的是相机姿态和3D点的位置,那么我们应该如何求解不同图像上的观测点呢?

显然我们在投影变换下,图像平面的二维点等于世界坐标系下的三维点乘上变换矩阵,并将变换后的齐次坐标转化为非齐次坐标得到,即 \(x^E = (\frac{m_1X}{m_3X},\frac{m_2X}{m_3X})^T\)
在仿射变换下也类似,但是由于仿射变换矩阵的最后一行为\([0,0,0,1]\),在齐次坐标下运算得到的 \(x\) 的最后一行也为 \(1\),从而将其转为非齐次坐标时我们能够得到更加直观的形式,即 \(x^E = AX^E+b\)
我们进一步关注仿射相机,在欧式空间中,求解仿射相机所需要的相关矩阵都是较为简单的,如图所示:

假设我们有了 \(m\) 个观测点的矩阵信息 \(x\),现在我们需要求解的是 \(A\) 和 \(X\) 和 \(b\),那么这里的 \(m\) 需要是多少才足够呢?
对于每个相机(共 \(m\) 个相机),都有一个对应的 \(A_i\) 矩阵。在仿射变换中, \(A_i\) 是 \(2×3\) 的矩阵,每个 \(A_i\) 矩阵包含 \(2×3=6\) 个元素。那么 \(m\) 个 \(A_i\) 矩阵总共的未知数数量就是 \(6m\) 个。
同样对于每个相机,都有一个对应的 \(b_i\) 向量。 \(b_i\) 是 \(2×1\) 的向量,每个 \(b_i\) 向量包含 \(2\) 个元素。所以 \(m\) 个 \(b_i\) 向量总共的未知数数量是 \(2m\) 个。
最后有 \(n\) 个固定的三维点 \(X_j\) ,每个三维点 \(X_j\) 有 \(3\) 个坐标值\((x,y,z)\),所以 \(n\) 个三维点的未知数数量是 \(3n\) 个。
将上述三部分的未知数数量相加: \(6m + 2m+3n=8m + 3n\) 。但由于存在一些自由度(例如,在仿射结构恢复中存在一些全局的尺度、旋转和平移等不确定性,通常可以消除 \(8\) 个自由度 ),所以最终的未知数数量是 \(8m + 3n - 8\) 个。
同时因为相机有 \(m\) 个,固定点有 \(n\) 个,那么相机 - 固定点的组合数为 \(m×n\) 组。因为每组组合能产生 \(2\) 个等式(二维坐标对应两个等式),所以一共能产生 \(2mn\) 个等式。
相当于我们需要用这 \(2mn\) 个等式来求解 \(8m + 3n - 8\) 个未知数。

这看起来是一个比较复杂的问题,目前常用的共有两种做法,一种是代数方法,即通过仿射极线几何来计算基础矩阵,从而得到相机参数;另一种则是因式分解方法,我们这里详细介绍这种方法。
A Factorization Method
这种方法由 Tomasi 和 Kanade 在 \(1992\) 年提出,核心步骤有两步:
\(\bullet\) 数据中心化(Data centering)
\(\bullet\) 因式分解(Factorization)
数据中心化
对于一组数据点,数据中心化是指将所有数据点的坐标进行平移,使得这些数据点的中心(通常是质心)移动到坐标原点。
首先我们需要计算观测点的均值,即 \(\overline{x}_i=\frac1n\sum_{k=1}^nx_{ik}\)
然后得到变换坐标为 \(\hat{x}_{ij}=x_{ij}-\overline{x}_i=x_{ij}-\frac1n\sum_{k=1}^nx_{ik}\)
我们将上面仿射变换的式子代入,有 \(\hat{x}_{ij}=x_{ij}-\frac1n\sum_{k=1}^nx_{ik}=A_iX_j+b_i-\frac1n\sum_{k=1}^nA_iX_k-\frac1n\sum_{k=1}^nb_i\)
将式子整理一下,得到 \(\hat{x}_{ij}=A_i(X_j-\frac1n\sum_{k=1}^nX_k)\)
可以发现,这里的 \(X_j-\frac1n\sum_{k=1}^nX_k\) 就是数据中心化的形式,所以我们可以进一步将式子写成 \(\hat{x}_{ij}=A_i\hat{X}_j\)
这样,在中心化后,每一个归一化的观测点都与3D点相关了,如果3D点的质心等于世界参考系的中心,那么式子就能进一步写成\(\hat{x}_{ij}=A_iX_j\)
因式分解
首先我们需要构造一个 \(2m×n\) 的测量矩阵 \(D\)

我们可以将这个测量矩阵重新写成两个矩阵相乘的形式,如图所示:

我们将由相机矩阵并起来的矩阵叫做运动矩阵,记为 \(M\),由3D点矩阵并起来的矩阵叫做结构矩阵,记为 \(S\),则 \(D=MS\),很容易得出 \(D\) 矩阵的秩为 \(3\)。
接下来我们需要考虑如何求解运动矩阵和结构矩阵,这里我们可以对 \(D\) 进行SVD分解,如图所示:

因为 \(D\) 矩阵的秩只有3,所以只有三个非 \(0\) 的奇异值 \(σ_1, σ_2, σ_3\),则我们就可以将无用的信息舍去,将D重新写为如下形式:

这里的 \(W_3\)是由三个奇异值按从大到小顺序构成的对角矩阵
从而 \(D=U_3W_3V_3^T=U_3(W_3T_3^T)=MS\),从而 \(M\) 矩阵就能等于 \(U_3\),\(S\) 矩阵就能等于 \(W_3V_3^T\)
但是在实际操作中,这种做法常常会遇到一些问题,因为由于测量中存在噪声或者仿射变换的过程中采用了近似,我们已知的 \(D\) 矩阵的秩可能大于 \(3\),所以这样的做法存在问题吗?

上图介绍了一个定理:在 Frobenius 范数的意义下,这种近似分解是最好的秩3近似,所以这种分解方法是合理的。
仿射歧义(Affine Ambiguity)

图中给出等式 \(D=MH×H^{-1}S\),其中 \(D\) 是测量矩阵,\(M\) 是相机矩阵,\(S\) 是三维点矩阵,\(H\) 是一个 \(3×3\) 的描述仿射变换的任意矩阵。该等式表明,通过引入 \(H\) 和其逆矩阵 \(H^{-1}\) ,可以得到新的相机矩阵 \(M^*=MH\) 和新的三维点矩阵 \(S^*=H^{-1}S\) 。
因此,测量矩阵 \(D\) 的分解不是唯一的。因为对于任意的 \(3×3\) 的仿射变换矩阵 \(H\) ,当对相机矩阵 \(M\) 应用变换 \(M^*=MH\) ,对三维点矩阵 \(S\) 应用变换 \(S^*=H^{-1}S\) 时,都能得到相同的测量矩阵 \(D\) 。这意味着,仅根据测量矩阵 \(D\) 进行分解,无法唯一确定相机矩阵 \(M\) 和三维点矩阵\(S\) ,存在多种可能的分解方式,这就是仿射歧义问题。
为了解决这种歧义性,必须施加额外的约束条件。通过添加特定的约束,如对相机的位置、姿态或三维点的分布等方面进行限制,才能从多种可能的分解中确定出符合实际情况的唯一解,从而准确地恢复出相机参数和三维点的位置信息。
相似性歧义(Similarity Ambiguity)
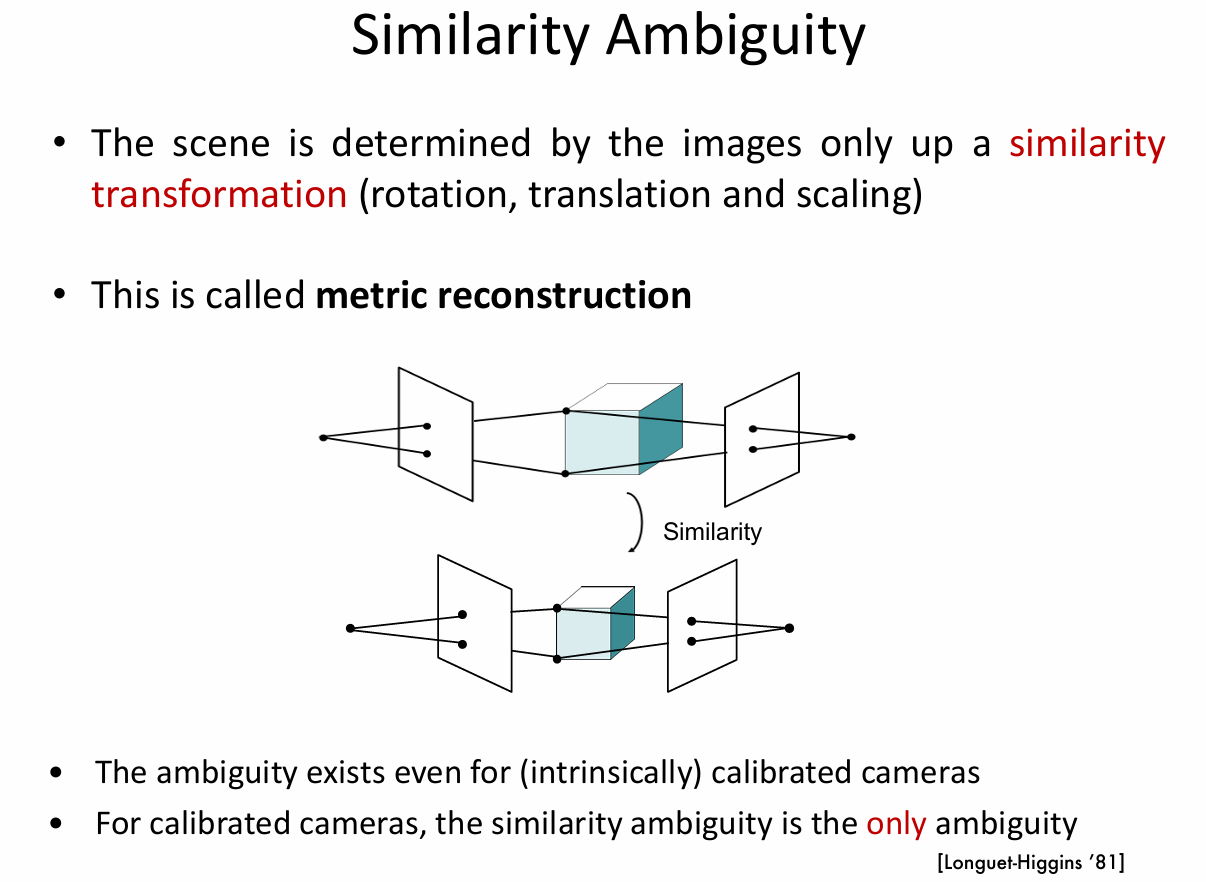
场景仅在相似性变换(包括旋转、平移和缩放)的程度上由图像确定。也就是说,通过图像进行场景重建时,只能确定场景在经过旋转、平移和缩放后的样子,而不能唯一确定其绝对的位置、姿态和大小。例如,一个物体在图像中呈现的样子,可能对应现实中经过不同旋转、平移和缩放后的多种实际情况,这种仅在相似性变换意义下由图像确定场景的重建方式被称为度量重建。
这种相似性歧义在已经标定的相机中仍然存在,而且需要注意的是,这种歧义是已标定相机唯一的歧义来源。这意味着,在相机内部参数已知的情况下,重建场景时仍然会因为相似性变换的不确定性而存在歧义,无法得到绝对精确的场景重建结果。