本文原在 2024-07-22 10:17 发布于本人洛谷博客。
一、定义与性质
1. 基本定义
从水厂出发,有很多节点和水管,节点不能存水,但容量无限,水管有容量上限,全部水管最终经过某些节点都会流向某个工厂里,问最多同时能给工厂发多少水?
流网络:这张图。
源点:水厂。
汇点:工厂。
弧:水管。
弧的流量:这条水管当前流多少水,对于弧 \((u,v)\) 用 \(f(u,v)\) 表示。
弧的容量:这条水管最多能流多少水,用 \(c(u,v)\) 表示。
弧的残量:这条水管还能流多少水,即 \(c(u,v)-f(u,v)\)。
流量网络/容量网络/残量网络:边权表示/流量/容量/残量的流网络。
(重要) 增广路:在残量网络中,还能从源点流向汇点的一条路径。
2. 性质
-
斜对称性:\(f(u,v)=-f(v,u)\)。
-
流量守恒:
- 对于节点,输出量和输入量相等。
- 源点的输出量等于汇点的输入量。
二、最大流
1. EK 算法
第一章第 1 节中所提到的问题就属于最大流问题。
基本思路就是:建一张容量网络,找到一条路径就给每条边减去相应的流量,并在剩下的残量网络上,不断找增广路。
但是对于下面这个图,显然找不到增广路了,但是肉眼可见最大流是 \(1\to 2\to 4\) 加上 \(1\to 3\to 4\)。
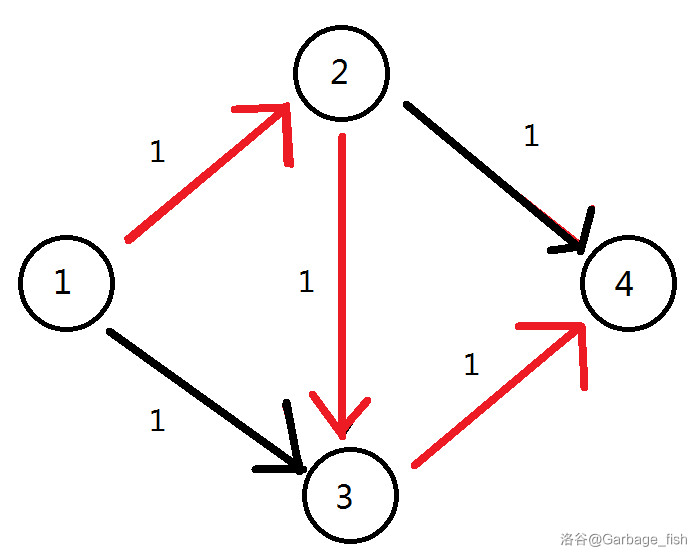
因此给程序一个反悔的机会:给每条边都建一条反向边(根据 \(0\oplus 1 =1\),\(1\oplus 0 = 0\);\(2\oplus 1 = 3\),\(3\oplus 1 = 2\);\(4\oplus 1 =5\)……的性质,可以用 \(i\) 和 \(i\oplus 1\) 作为一组相反的边),边权表示正向边的流量,实时更新。
每次找到一条路径后,给路径上的边减去本路径的最大流,路径上的反边加上本路径的最大流。这样就会发现:如果路径中含有一条反向边,它恰好能将正向边的容量给推回去。
int bfs() { // bfs寻找增广路for (int i = 1; i <= n; i++)vis[i]=0;queue<int> q;q.push(s);vis[s] = 1;dis[s] = oo;while (!q.empty()) {int u = q.front();q.pop();for (int i = head[x]; i; i = edge[i].next) {if (edge[i].flow == 0)continue;// 如果是正向边:没有残量了怎么流?如果是反向边:正向边没有流量怎么流?int v = edge[i].v;if (vis[v])continue; // 访问过了flow[v] = min(flow[u], edge[i].flow);// 显然,一条路径的最大流取决于能流最小的那条边pre[v] = i; // 记录前驱,方便修改边权 q.push(v);vis[v] = 1;if (v == t)return 1; // 找到了一条增广路 }}return 0;
}void update() { // 更新所经过边的正向边权以及反向边权 int u = t;while (u != s) {int v = pre[u];edge[v].flow -= flow[t];edge[v ^ 1].flow += flow[t];u = edge[v ^ 1].v;}maxflow += flow[t]; // 累加每一条增广路经的最小流量值
}
void EK() {while (bfs())update();
}
2. Dinic 算法
EK 算法一次才找一条增广路,使用 Dinic 算法的 DFS 可以一次寻找多条增广路。
用 BFS 对图分层,作用在于一次可以得到多条长度相同的最短增广路。
每次从当前点出发,选用从当前点所在层到下一层的边,发送一定的流量,流量的大小取边残量和当前点从源点获取的剩余流中两者的最小值。
搜索完成后,返回一个流量值,即这条增广路的流量,此时就能够对边和反向边的残量进行更新了。
bool bfs() {fill(dis, dis + N, oo);queue<int> q;q.push(s);dis[s] = 0;now[s] = head[s];while (!q.empty()) {int u = q.front();q.pop();for (int i = head[u]; i; i = edge[i].next) {int v = edge[i].v;if (edge[i].w <= 0 or dis[v] != oo)continue;q.push(v);now[v] = head[v]; // 记录当前弧优化,可以不写,直接用 headdis[v] = dis[u] + 1; // 分层if (v == t) // 到汇点了return true;}}return false;
}
int dfs(int u, int last) {if (u == t) return last; // 到汇点了int ret = 0;for (int i = now[u]; i and last; i = edge[i].next) {now[u] = i;int v = edge[i].v;if (edge[i].w <= 0 or dis[v] != dis[u] + 1) // 没有流量或者层数对不上continue;int tmp = dfs(v, min(last, edge[i].w)); // 往后走的最大流if (!tmp) dis[v] = oo;edge[i].w -= tmp;edge[i ^ 1].w += tmp;ret += tmp;last -= tmp;}return ret;
}
void dinic() {while(bfs())ans += dfs(s, oo);
}
三、费用流
以最小费用最大流为例:
每条水管要收费,假设水管 \((u,v)\) 的单价是 \(cost\),那么你就要付 \(f(u,v)\times cost\)。
将 EK 算法的 BFS 改成 SPFA 即可,可能有负边不能 Dijkstra。
namespace McMf {int cost[N], flow[N], pre[N];bool vis[N];bool spfa() {queue<int> q;fill(cost, cost + N, oo);memset(vis, 0, sizeof vis);q.push(s);cost[s] = 0;vis[s] = true;flow[s] = oo;while (!q.empty()) {int u = q.front();q.pop();vis[u] = false;for (int i = head[u]; i; i = edge[i].next) {if (!edge[i].flow)continue;int v = edge[i].v;if (cost[v] > cost[u] + edge[i].cost) {cost[v] = cost[u] + edge[i].cost;flow[v] = min(flow[u], edge[i].flow);pre[v] = i;if (!vis[v]) {q.push(v);vis[v] = true;}}}}return cost[t] <= oo / 2;}void mcmf() {while (spfa()) {int u = t;maxflow += flow[u];mincost += flow[u] * cost[u];while (u != s) {int p = pre[u];edge[p].flow -= flow[t];edge[p ^ 1].flow += flow[t];u = edge[p ^ 1].v;}}}
}
using namespace McMf;
四、上下界网络流
1. 无源汇上下界可行流
假设上下界是 \([L,R]\),点 \(x\) 流入的量是 \(in_x\),流出的量是 \(out_x\)。
令每条边都先流自己的 \(L\),统计到 \(in_x\) 和 \(out_x\) 中,然后构造一个流网络,边权为 \(R-L\)。
如果 \(in_x>out_x\),那么建边 \((s,x,in_x-out_x)\)。
如果 \(in_x<out_x\),那么建边 \((x,t,out_x-in_x)\)。
在这个新构造的流网络中,如果源点流出的每一条边都能流满,那么说明流量平衡。
2. 有源汇上下界可行流
连接题目给出的源点 \((t,s,[0,\infty])\),用 1 的方法。
3. 有源汇上下界最大流
跑完可行流后,在残量网络中找 \(s\to t\) 的最大流。
#include <bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
const int N = 1e6 + 10, oo = 1e18;
int n, m, s, t, s1, t1, in[N], out[N], over;
int head[N], ide = 1;
struct EDGE {int v, next, w;
} edge[N];
void add(int u, int v, int w) {edge[++ide] = {v, head[u], w};head[u] = ide;edge[++ide] = {u, head[v], 0};head[v] = ide;
}
int dis[N], now[N];
bool bfs() {fill(dis, dis + N, oo);queue<int> q;q.push(s);dis[s] = 0;now[s] = head[s];while (!q.empty()) {int u = q.front();q.pop();for (int i = head[u]; i; i = edge[i].next) {int v = edge[i].v;if (edge[i].w <= 0 or dis[v] != oo)continue;q.push(v);now[v] = head[v];dis[v] = dis[u] + 1;if (v == t)return true;}}return false;
}
int dfs(int u, int last) {if (u == t)return last;int ret = 0;for (int i = now[u]; i and last; i = edge[i].next) {now[u] = i;int v = edge[i].v;if (edge[i].w <= 0 or dis[v] != dis[u] + 1)continue;int tmp = dfs(v, min(last, edge[i].w));if (!tmp)dis[v] = oo;edge[i].w -= tmp;edge[i ^ 1].w += tmp;ret += tmp;last -= tmp;}return ret;
}
int dinic() {int ret = 0;while(bfs())ret += dfs(s, oo);return ret;
}
signed main() {IOS;cin >> n >> m >> s1 >> t1;s = n + 1, t = n + 2;for (int i = 1, u, v, lb, ub; i <= m; i++) {cin >> u >> v >> lb >> ub;in[v] += lb, out[u] += lb;add(u, v, ub - lb);}for (int i = 1; i <= n + 2; i++)if (in[i] > out[i]) {add(s, i, in[i] - out[i]);over += in[i] - out[i];} elseadd(i, t, out[i] - in[i]);add(t1, s1, oo);if (dinic() != over) {cout << "please go home to sleep";return 0;}s = s1, t = t1;cout << dinic();return 0;
}
4. 有源汇上下界最小流
求出可行流,把 \((t,s,[0,\infty])\) 删掉,再跑一次,前后两次相减。