为什么stereo很有用?
当我们需要从单一视角恢复结构时,我们的信息来源有以下几种:
\(\bullet\) 从标定架可以获取标定架的位置 / 姿态以及相机内参 K。
\(\bullet\) 从无穷远点和线,加上正交的线和平面等信息,可以获取场景的结构和相机内参 K 。
但是由于内在歧义性,从单一的视角恢复结构非常困难,但是如果我们引入stereo-view这个问题就会变得容易。
三角测量
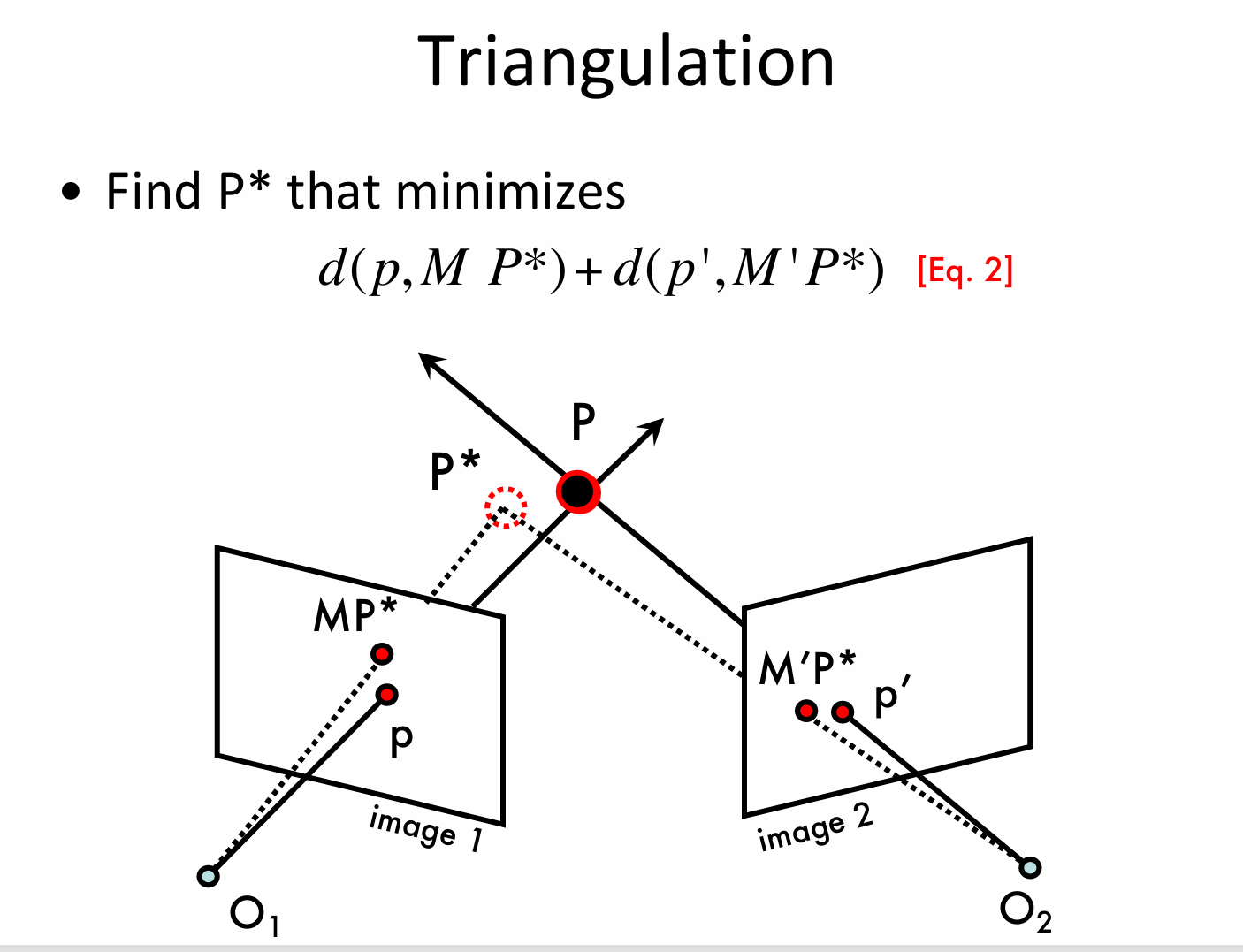
三角测量是一种能够根据不同视角图像的对应点来确定3D点的位置的方法,他的测量原理如下:
存在两个相机中心 \(\mathbf{O_1}\) 和 \(\mathbf{O_2}\),分别对应图像的 \(image1\) 和 \(image2\)。
三维空间中有一个真实点 \(P\),它在图像 \(image 1\) 上的投影为 \(p\),在图像 \(image 2\) 上的投影为 \(p'\)。
\(P^*\) 是对真实点 \(P\) 的一个估计,\(MP^*\) 是 \(P^*\) 在图像 \(image 1\) 上的投影位置,\(M'P^*\) 是 \(P^*\) 在图像 \(image 2\) 上的投影位置。通过最小化上述距离之和,来优化对空间点 \(P\) 的估计 \(P^*\) ,从而实现从两个不同视角图像中的对应点来确定三维空间点的位置。
通过这种方法,我们能够解决多视角几何中的很多问题。
多视图(立体)几何(Multi (stereo)-view geometry)
在多视图几何中,我们需要解决的是三个核心问题:
相机几何(Camera geometry)
给定两张图像中的对应点,找到相机矩阵、位置和姿态。这意味着通过不同图像上的对应点信息,来确定相机在空间中的参数和状态,有助于理解相机的观测角度和位置关系。
场景几何(Scene geometry)
从三维点在两张或多张图像中的投影,找到该三维点的坐标。这是基于多视图的投影信息,反向推导出空间中三维点的位置,是三维重建等任务的重要基础。
对应关系(Correspondence)
给定一张图像中的点 p,如何在另一张图像中找到对应的点 p'。这是多视图几何中的关键问题之一,准确找到对应点对于后续的相机参数计算和三维场景重建等操作至关重要。
为了更好地去解决这些问题,我们引入了对极几何的概念。
对极几何(Epipolar geometry)

首先我们需要介绍一些重要概念:
\(\bullet\) 基线(Baseline):连接两个相机中心 \(\mathbf{O_1}\) 和 \(\mathbf{O_2}\) 的黄色线段称为基线。
\(\bullet\) 对极平面(Epipolar Plane):由点 \(P\) 和基线 \(\mathbf{O_1O_2}\) 所构成的灰色平面称为对极平面。
\(\bullet\) 对极点 \(e\),\(e'\)(Epipoles):基线 \(\mathbf{O_1O_2}\) 与左右图像平面的交点分别为 \(e\) 和 \(e'\),这两个点称为对极点,同时它们也是另一个相机中心在当前图像平面上的投影。
\(\bullet\) 对极线(Epipolar Lines):连接 \(p\) 与 \(e\) 的蓝色线段以及连接 \(p'\) 与 \(e'\) 的蓝色线段称为对极线。
平行图像平面的对极几何
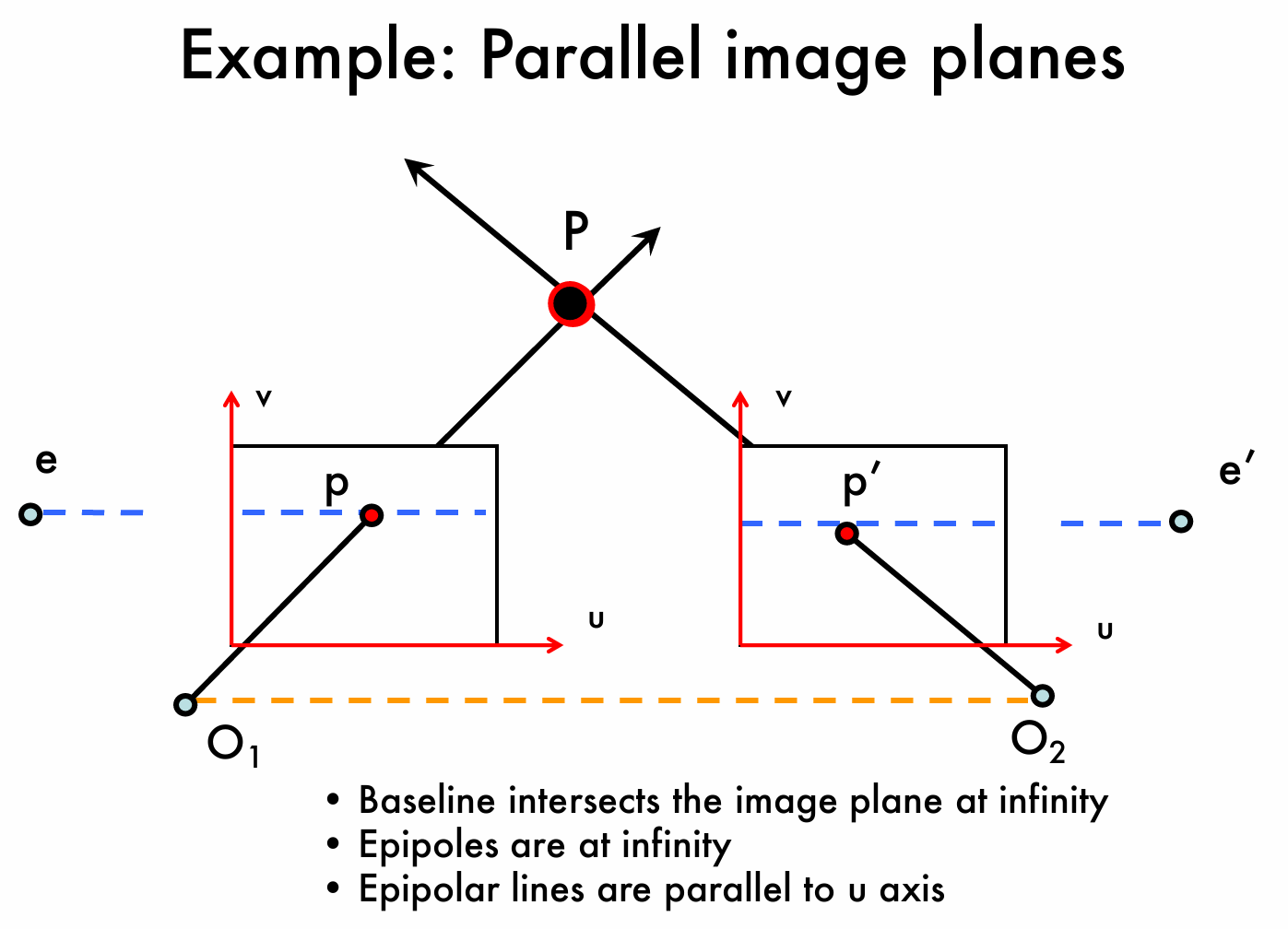
对于平行平面,他具有一些特殊的性质,例如基线与图像平面在无穷远处相交,对极点位于无穷远处,对极线平行于 \(u\) 轴等,这些性质有助于简化对应点匹配等计算机视觉任务的计算和分析。
向前平移

向前平移是一种特殊的相机运动模式,它的对极几何也具有一些独特的性质,例如对极点在两个图像中具有相同的位置(可以视作平移),同时对极线汇聚到同一点,也即是对极点,此对极点也被称为扩展焦点(Focus of Expansion,FOE)。
接下来我们要介绍如何利用对极几何解决问题,一个很常见的问题是对极约束:对于同一对象的两个视图,给定左侧图像上的点,如何在右侧图像上找到相应的点呢?
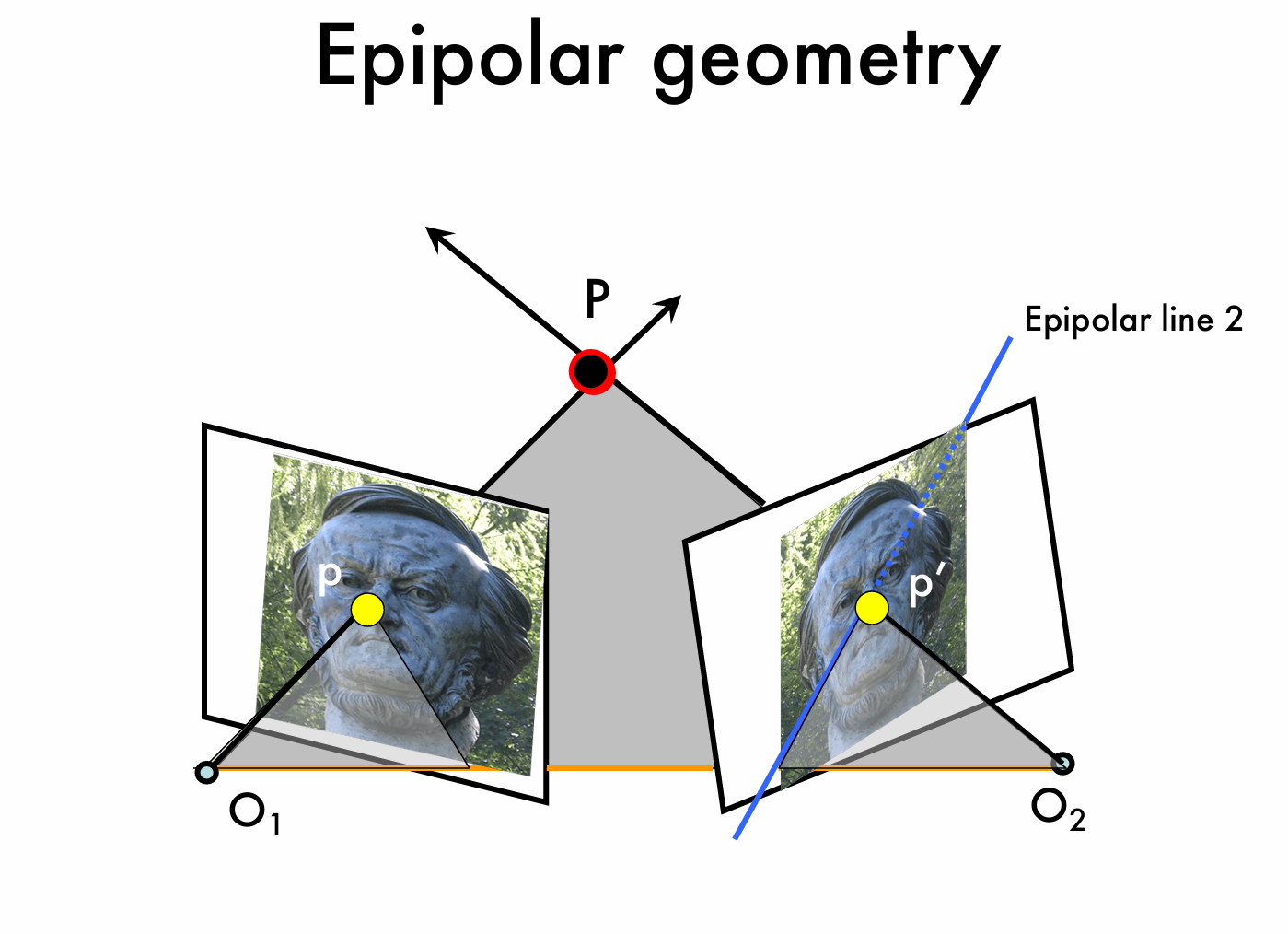
转化到对极几何上就是形如上图所示,已知左侧图像的对极点,要求解右侧图像的对极点。
对极约束(Epipolar Constraint)
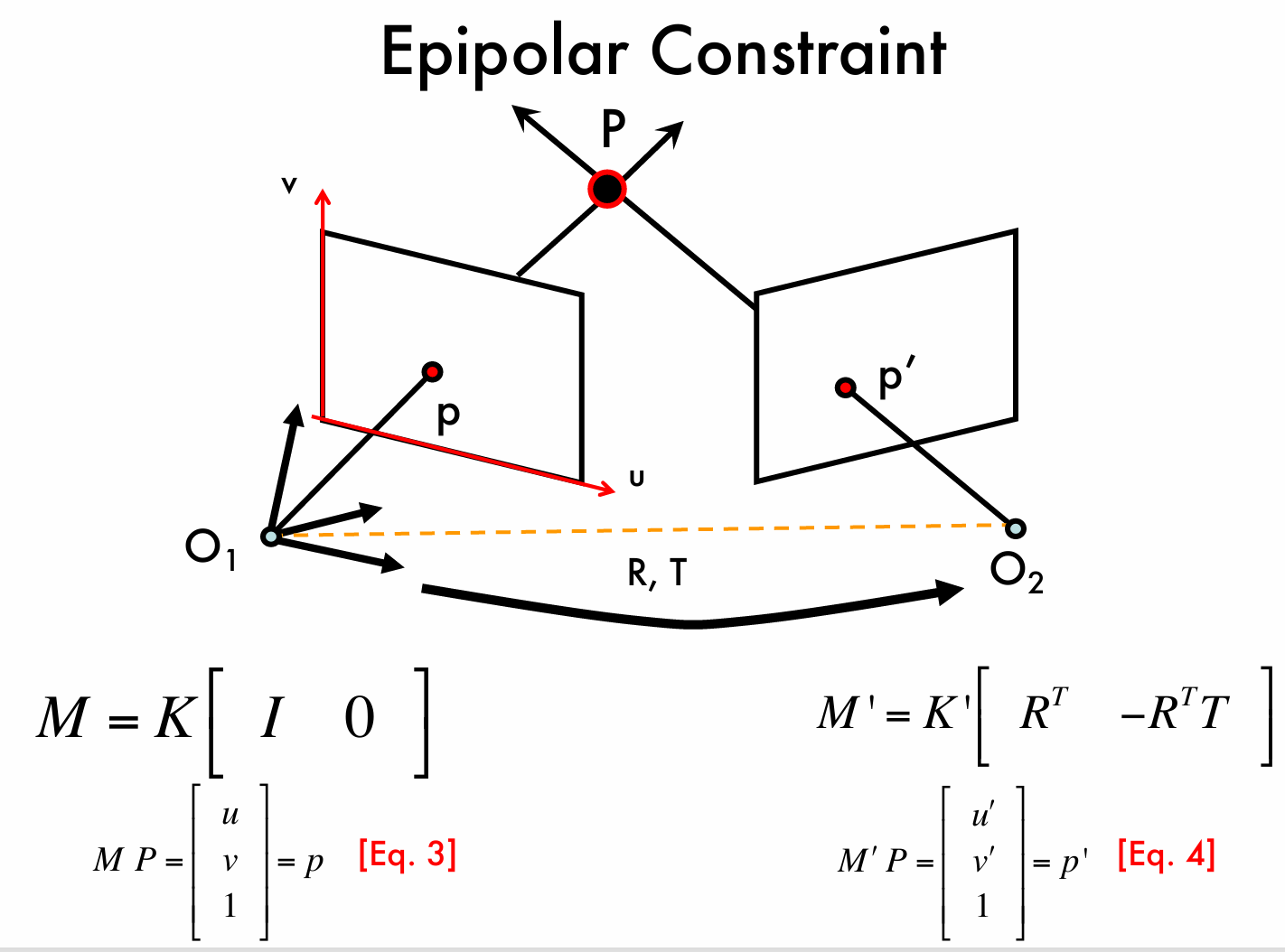
左侧定义了相机 \(O_1\) 的投影矩阵 \(M = K\begin{bmatrix} I & 0 \end{bmatrix}\),其中 \(K\) 是相机内参矩阵,\(I\) 是单位矩阵,\(0\) 是零矩阵。通过投影矩阵 \(M\) 对三维点 \(P\) 进行投影得到图像点 \(p\),即 \(MP = \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = p\) 。
右侧定义了相机 \(O_2\) 的投影矩阵 \(M' = K'\begin{bmatrix} R^T & -R^TT \end{bmatrix}\),其中 \(K'\) 是相机 \(O_2\) 的内参矩阵,\(R^T\) 是旋转矩阵 \(R\) 的转置。通过投影矩阵 \(M'\) 对三维点 \(P\) 进行投影得到图像点 \(p'\),即 \(M'P = \begin{bmatrix} u' \\ v' \\ 1 \end{bmatrix} = p'\) ,我们用上述公式描述了两个相机之间的相对位姿关系。
为了让问题更加简单,我们这里认为两个相机均为标准相机,其内参矩阵为 \(K_{canonical}=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}\) 。从而我们能够把投影矩阵进行化简,即相机 \(O_1\) 的投影矩阵简化为 \(M = \begin{bmatrix}I&0\end{bmatrix}\),相机 \(O_2\) 的投影矩阵简化为 \(M' = \begin{bmatrix}R^T& -R^TT\end{bmatrix}\)
接下来课程中给出了两个公式,如图所示,这里的公式推导困扰了笔者很久,现在我们详细讲一下公式是怎么推导出来的。
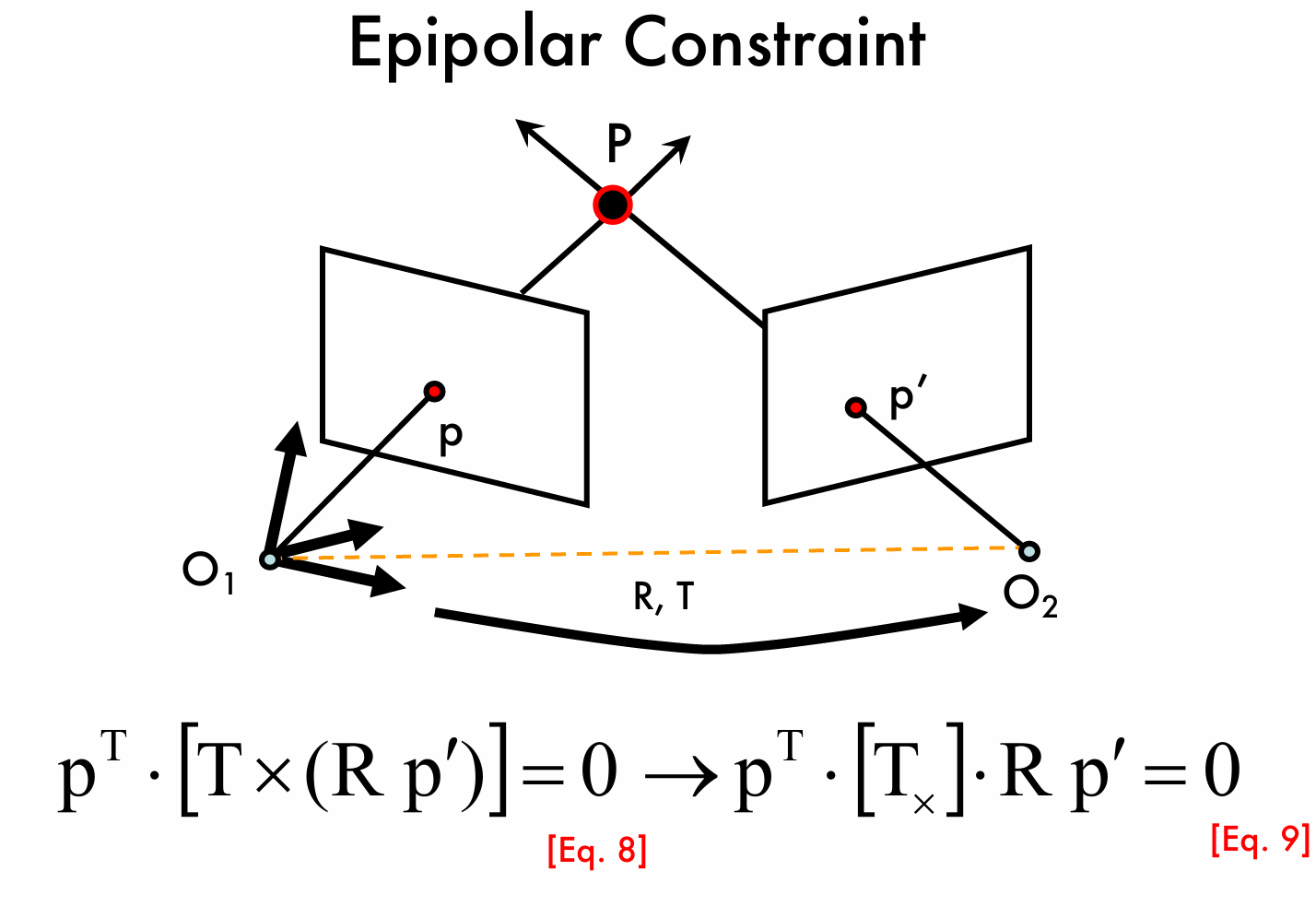
首先我们先思考一下 \(p'\) 的含义,他是我们通过第二个相机得到的投影点,为了求解对极约束条件,我们需要将这个点与第一个相机联系起来。由于我们这里认为两个相机均为标准相机,因此第二个相机可以认为是由第一个相机经历旋转和平移得到的,如图所示:
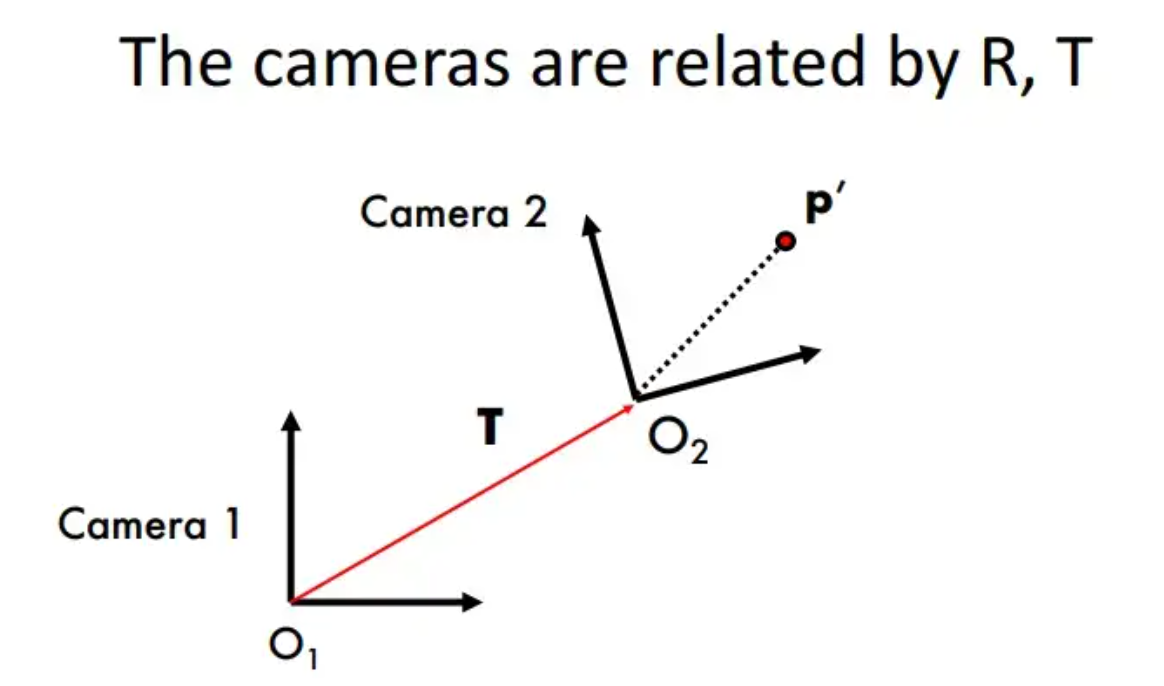
因此我们可以得到 \(p=R(p'-T)\),由于 \(R\) 是正交矩阵,因此可以写做 \(p'-T=R^{-1}p=R^Tp\),同时因为三个向量共面,由于混合积表示有向体积,则混合积为零,则有 \((R^Tp')^T·T×p=0\),即有 \((p'^TR)·(T×p)=0\),交换 \(p\) 和 \(p'\) 的位置即可得到上述公式,即 \((p^T)·(T×(Rp'))=0\)。
将向量叉乘写成矩阵形式,则有 \(p^T·{[T_×]}·Rp'=0\),我们把式子中的 \({[T_×]}·R\) 记作 \(E\),叫做本质矩阵。
进一步地,我们能够得到更多的对极约束:
\(\bullet\) \(l=Ep'\)是与 \(p'\) 相关联的对极线,意味着已知右图像上的点 \(p'\),通过本质矩阵 \(E\) 可得到左图像上对应的对极线 \(l\) 。
\(\bullet\) \(l' = E^{T} p\) 是与 \(p\) 相关联的对极线,即已知左图像上的点 \(p\),通过 \(E\) 的转置 \(E^{T}\) 可得到右图像上对应的对极线 \(l'\)
\(\bullet\) \(E e' = 0\) 和 \(E^{T} e = 0\) ,表明本质矩阵 \(E\) 与对极点 \(e\)、\(e'\) 的关系,对极点是基线与图像平面的交点。
\(\bullet\) \(E\) 是一个 \(3\times3\) 的矩阵,具有 5 个自由度。这是因为本质矩阵由旋转矩阵 \(R\) 和平移向量 \(T\) 决定,而 \(R\) 有 3 个自由度,\(T\) 有 3 个自由度,但存在尺度等价性,所以总共 5 个自由度。
\(\bullet\) \(E\) 是奇异矩阵,秩为 2。这是由其内在的几何性质决定的,反映了对极几何中的一些约束关系。
我们注意到一个问题,上面的讨论中,我们假设相机的内部参数是一致的。真实情况可能并不是这样(如焦距变化)。下面在考虑内部参数变化基础上,做进一步探讨。
我们所要做的工作很简单——把内部参数矩阵K考虑进去,按照上面的推导过程再来一遍。这里我们省略了推导过程,直接给出结论:
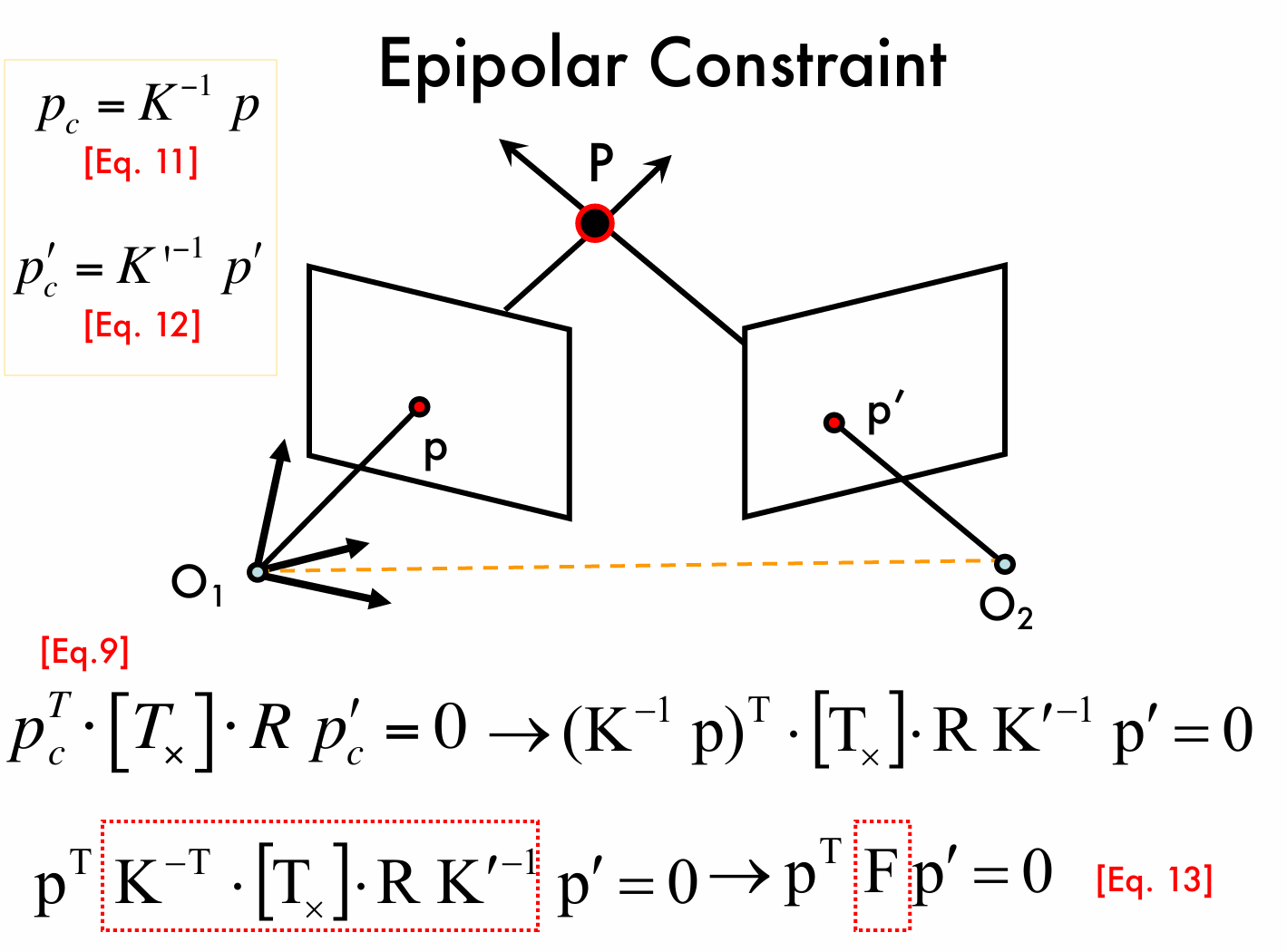
与本质矩阵的定义类似,由于 \(p^TK^{-T}·[T_×]·RK'^{-1}p'=0\),我们令 \(F=K^{-T}·[T_×]·RK'^{-1}\),得到与前面类似的形式,即 \(p^TFp'=0\),我们称 \(F\) 为基础矩阵。
类似的,我们也能得到相关的对极约束:
\(\bullet\) \(l=Fp'\)是与 \(p'\) 相关联的对极线,意味着已知右图像上的点 \(p'\),通过基础矩阵 \(F\) 可得到左图像上对应的对极线 \(l\) 。
\(\bullet\) \(l' = F^{T} p\) 是与 \(p\) 相关联的对极线,即已知左图像上的点 \(p\),通过 \(F\) 的转置 \(F^{T}\) 可得到右图像上对应的对极线 \(l'\)
\(\bullet\) \(F e' = 0\) 和 \(F^{T} e = 0\) ,表明基础矩阵 \(F\) 与对极点 \(e\)、\(e'\) 的关系,对极点是基线与图像平面的交点。
\(\bullet\) \(F\) 是一个 \(3\times3\) 的矩阵,具有 7 个自由度。这是因为基础矩阵综合了相机的内参和相对位姿信息,相比本质矩阵多了相机内参的影响,所以有 7 个自由度。
\(\bullet\) \(F\) 是奇异矩阵,秩为 2。这是由其内在的几何性质决定的,反映了对极几何中的一些约束关系。
在实际应用中,基础矩阵 \(F\) 非常有用,因为假设我们已经知道了 \(F\),我们仅需要知道左图中的一个点,不需要额外的信息,我们就能计算出第二幅图中与该点对应的极线,即 \(l'=F^Tp\)。
八点法
接下来我们介绍一下如何计算基础矩阵 \(F\), 这里我们使用八点法进行求解。
根据公式 \(p^TFp'=0\),我们将公式展开,其中 \(p = \begin{bmatrix}u \\ v \\ 1\end{bmatrix}\) 和 \({p}' = \begin{bmatrix}u' \\ v' \\ 1\end{bmatrix}\) 分别是两个图像中对应点的齐次坐标,\(F = \begin{bmatrix}F_{11} & F_{12} & F_{13} \\ F_{21} & F_{22} & F_{23} \\ F_{31} & F_{32} & F_{33}\end{bmatrix}\) 是基础矩阵,则有
\(
\begin{align*}
(u, v, 1) \begin{bmatrix}F_{11} & F_{12} & F_{13} \\ F_{21} & F_{22} & F_{23} \\ F_{31} & F_{32} & F_{33}\end{bmatrix} \begin{bmatrix}u' \\ v' \\ 1\end{bmatrix} &= 0 \\
\end{align*}
\)
进一步得到 \((uu', uv', u, vu', vv', v, u', v', 1) \begin{bmatrix}F_{11} \\ F_{12} \\ F_{13} \\ F_{21} \\ F_{22} \\ F_{23} \\ F_{31} \\ F_{32} \\ F_{33}\end{bmatrix} = 0\)。
我们发现,基础矩阵 \(F\) 是一个 \(3×3\)的矩阵,有 \(9\) 个未知元素。然而,上面的公式中使用的齐次坐标,齐次坐标在相差一个常数因子下是相等,F也就只有 $8 $个未知元素,也就是说,只需要 \(8\) 对匹配的点对就可以求解出两视图的基础矩阵F。
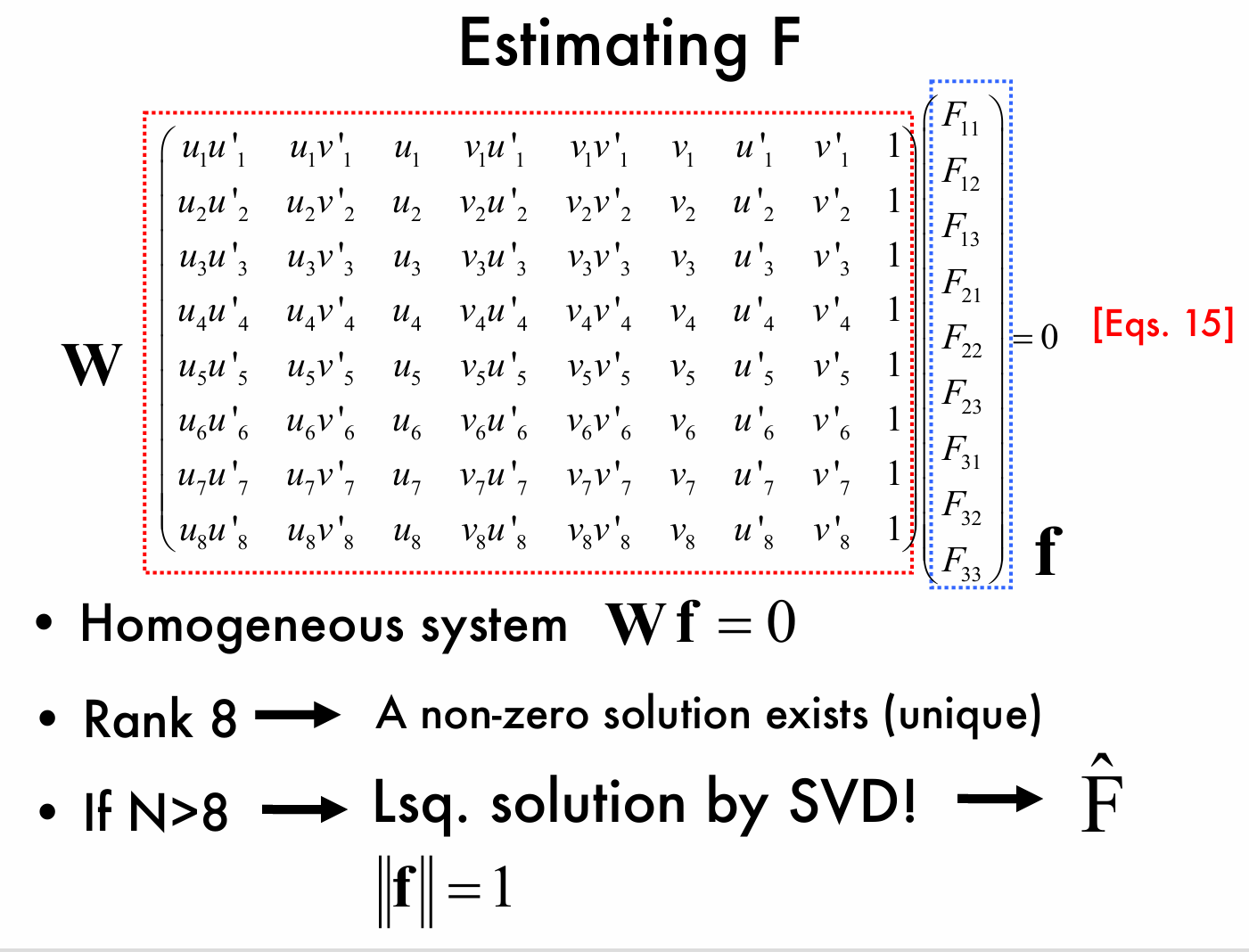
我们需要把 \(8\) 组对应点中的每一组点的坐标组合,例如第一行是 \((u_1u_1', u_1v_1', u_1, v_1u_1', v_1v_1', v_1, u_1', v_1', 1)\) ,这里 \((u_1, v_1)\) 和 \((u_1', v_1')\) 是第一组对应点在两个图像中的坐标,以此类推,共 8 组对应点,进而形成一个 \(8×9\) 的矩阵 \(W\)。
所以求解基础矩阵 \(F\) 我们只需要解一个齐次线性方程组 \(\mathbf{Wf}=0\),当矩阵 \(\mathbf{W}\) 的秩为 8 时,根据线性代数知识,此齐次方程组存在非零解(且唯一,在相差一个尺度因子的意义下)。
如果对应点的数量 \(N > 8\) ,此时可以通过奇异值分解的方法来求解最小二乘解,从而估计出基础矩阵 \(\hat{F}\) 。同时,为了使解具有唯一性(去除尺度模糊性),通常会对向量 \(\mathbf{f}\) 进行归一化处理,使其范数 \(\|\mathbf{f}\| = 1\) 。
这里有一些问题需要注意,通过之前方法估计出的 \(\hat{F}\) 可能是满秩的(即 \(\text{det}(\hat{F}) \neq 0\) )。但需要记住的是,理论上基础矩阵 \(F\) 的秩为 2(Rank2),这是由其内在的对极几何性质决定的。
为了使估计的矩阵符合基础矩阵的理论性质,需要找到一个矩阵 \(F\) ,使得在弗罗贝尼乌斯范数下,\(\| F - \hat{F} \| = 0\) 最小化,即找到与估计矩阵 \(\hat{F}\) 最接近的矩阵 \(F\) 。同时,\(F\) 要满足约束条件 \(\text{det}(F) = 0\) ,以保证其秩为 2。
因此,可以再次使用奇异值分解来解决这个优化问题。弗罗贝尼乌斯范数是矩阵中所有元素平方和的平方根,通过 SVD 对矩阵进行分解和处理,能够在满足秩为 2 的约束下,找到最接近估计矩阵 \(\hat{F}\) 的基础矩阵 \(F\) 。
对估计矩阵 \(\hat{F}\) 进行奇异值分解,得到 \(\hat{F} = U\begin{bmatrix}s_1 & 0 & 0 \\ 0 & s_2 & 0 \\ 0 & 0 & s_3\end{bmatrix}V^T\) ,其中 \(U\) 和 \(V\) 是正交矩阵,\(\begin{bmatrix}s_1 & 0 & 0 \\ 0 & s_2 & 0 \\ 0 & 0 & s_3\end{bmatrix}\) 是由奇异值 \(s_1, s_2, s_3\) 构成的对角矩阵。
为使 \(F\) 满足秩为 2 的条件,构建满足要求的基础矩阵 \(F = U\begin{bmatrix}s_1 & 0 & 0 \\ 0 & s_2 & 0 \\ 0 & 0 & 0\end{bmatrix}V^T\) ,即将 \(\hat{F}\) 奇异值分解结果中的最小奇异值 \(s_3\) 设为 0,这样得到的 \(F\) 行列式为 0,秩为 2,且在弗罗贝尼乌斯范数下与 \(\hat{F}\) 尽可能接近。
但是八点法也存在一些问题:
\(\bullet\) 高度不平衡(条件数差):八点算法得到的方程组 \(\mathbf{Wf} = 0\) 具有高度不平衡性,即矩阵 \(\mathbf{W}\) 是病态的。这意味着矩阵的条件数很大,对输入数据的微小变化非常敏感。
\(\bullet\) 矩阵元素幅值要求:矩阵 \(\mathbf{W}\) 中元素的值必须具有相似的数量级。如果元素幅值差异过大,会影响后续计算的稳定性和准确性。
\(\bullet\) 对奇异值分解的影响:上述问题会在对矩阵 \(\mathbf{W}\) 进行奇异值分解时产生问题。因为 SVD 对矩阵的条件数和元素特性较为敏感,病态的矩阵可能导致分解结果不准确或不稳定,从而影响基础矩阵的估计精度。
归一化八点法
为了解决八点法中存在的问题,我们对该方法进行了一些改进:核心思路是对图像坐标进行变换,使矩阵 \(\mathbf{W}\) 具有更好的条件数(即改善其病态性),这一过程也称为预处理。通过这种方式,可以提升后续计算的稳定性和准确性。
对于每一幅图像,应用一个变换 \(T\) ,该变换包含平移(translation)和缩放(scaling)操作,作用于图像坐标,需满足以下两个条件:
坐标原点设置:将图像点的质心设为坐标原点。这样做可以使坐标分布更加集中,消除因坐标原点选取不当导致的偏差。
距离约束:使图像点到原点的均方距离约为 2 像素。通过缩放操作实现这一约束,能让坐标值的数量级保持在合适范围,避免因坐标值过大或过小引起的矩阵 \(\mathbf{W}\) 元素幅值差异过大问题,从而改善矩阵的条件数,提升八点算法中奇异值分解等后续计算的稳定性和精度。
以下图为例,我们将图像变换前后进行对比:左侧图像展示了应用变换 \(T\) 之前的图像坐标系,图中是一尊雕像的照片,雕像面部区域有多个彩色的点,这些点代表图像中的特征点。黄色虚线圆表示特征点的分布范围。此时的坐标系原点位置不特殊,特征点分布较为随意;右侧图像展示了应用变换 \(T\) 之后的图像坐标系。经过变换后,图像点的质心成为了坐标原点,并且图像点到原点的均方距离约为 2 像素。彩色点的分布相对更加集中,且围绕在新的原点周围。
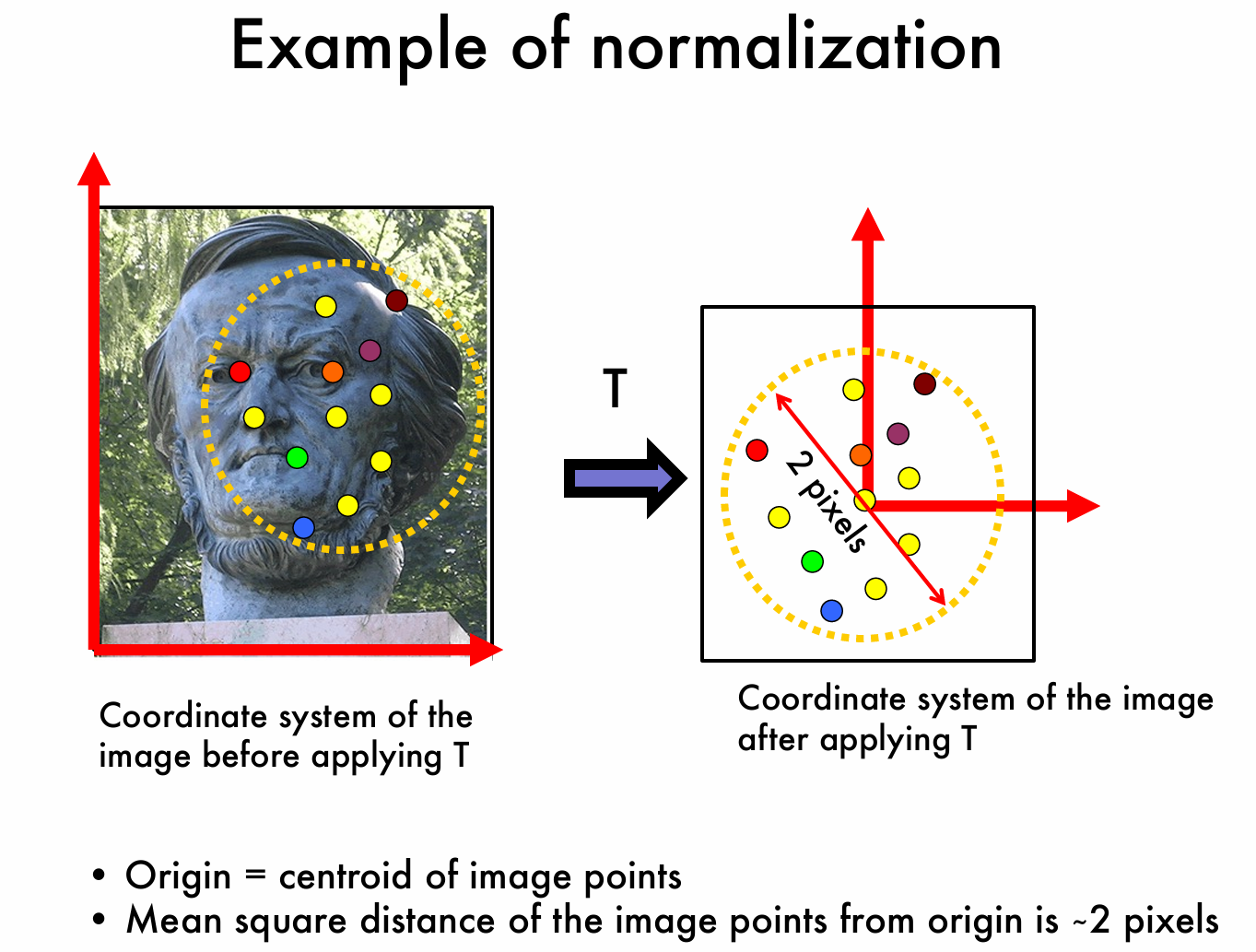
如果将原来的图像记为 \(p_i\) 和 \(p’_i\),变换后的图像记为 \(q_i\) 和 \(q'_i\),则有 \(q_i=Tp_i\) 和 \(q'_i=Tp'_i\)。
所以我们总结一下归一化八点法的算法流程:
1.分别计算图像 1 和 2 的 \(T\) 和 \(T'\)
2.归一化图 1 和图 2 中的坐标:\(q_i=Tp_i\) 和 \(q'_i=Tp'_i\)
3.使用八点法从对应点 \(q\) 和 \(q'\) 计算 \(\hat{F}_q\)
4.约束 \(F_q\) 满足秩2的限制,即让 \(q^TF_qq'=0\) 且 \(\text{det}(F_q) = 0\)
5.重新归一化 \(F_q\) 得到\(F\),即 \(F=T^TF_qT'\)
以上就是本文全部内容,如有错误,请指正。