这或许是这几天的济南云斗集训之旅最大的收获吧,若是最后一天的模拟赛文件不会交错也许结局会更好,但在这残酷的现实中却从不会有“如果”一词,母亲以不想让我学了,或许考完今年的 CSP 就可能不学了吧。
本文将效仿《李煜东算法进阶指南》的思路,按照例题层层深入。
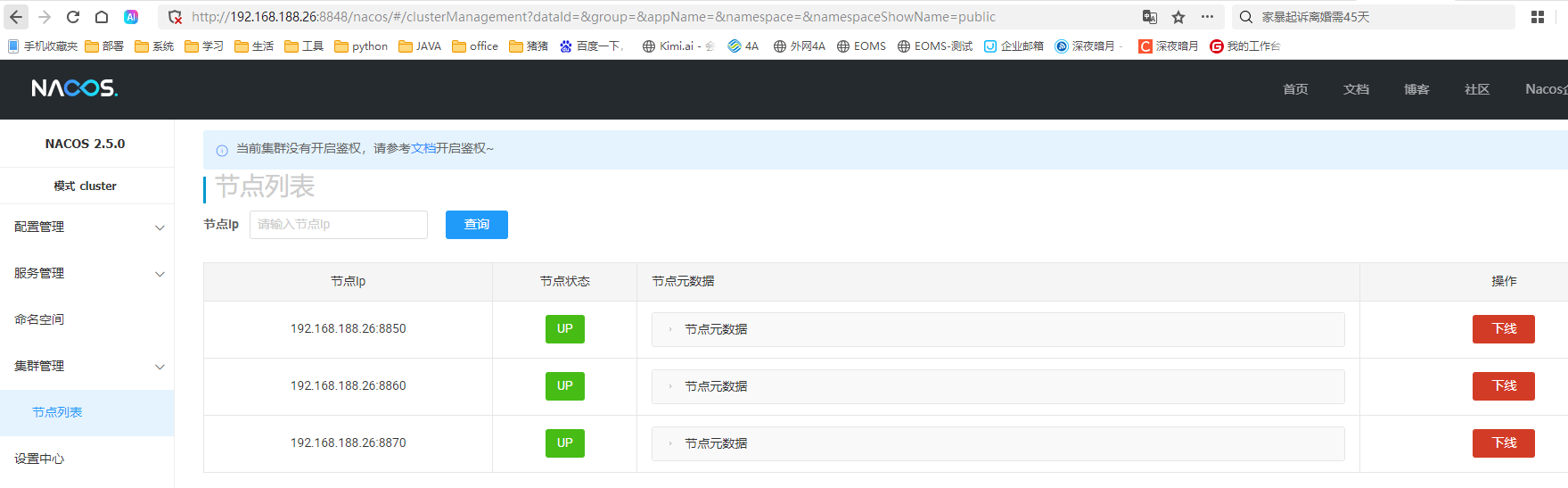
P2365 任务安排
题目链接
凡是先考虑朴素算法,这是一个好习惯。
朴素的解法
求出 \(T,C\) 的前缀 \(t,c\),设 \(f_{i,j}\) 为把前 \(i\) 个任务分为 \(j\) 批的最小费用,明显的是第 \(j\) 批任务完成的时间为第 \(j\times S+t_i\) 时刻。
朴素的解法复杂度 \(O(n^3)\)。
本题正解
思考为什么要 \(j\) 这一维,发现 \(j\) 这一维完全是为了求当前这一批完成的时刻。
思考该如何优化,感觉不容易直接求之前此机器启动过几次,但机器每次启动所耗费的时间 \(S\) 最终会累积到之后所有任务完成时间上。所以我们可以将其累加到费用当中。
设 \(f_i\) 表示把前 \(i\) 个任务分成若干批执行的最小费用,状态转移方程为:
下文摘自《李煜东算法进阶指南》:
也就是说我们没有直接求出每批的完成时刻,而是在一批任务“开始”对后续任务产生影响时,就先把费用累加到答案中。这是一种名为“费用前提计算”的经典思想。
很明显这段话可谓相当的晦涩。
该复杂度 \(O(N^2)\)。
咦,好尴尬,我似乎没有写过关于此解的的代码。
P10979 任务安排 2
题目链接
与上一题的题意一模一样,但数据加强了。
将上一题的转化方程拆一下,得:
由于 \(f_i\) 的大小只与跟 \(j\) 有关的项有关,其他项都是固定的,可以当作常数,然后再合并同类项,于是得:
让我们把 \(min\) 函数去掉,然后将全部不与 \(j\) 有关的项作为常数项(包括 \(f_i\)),将与 \(j\) 有关的项当作变量,组成一个函数式:
在一个以 \(c_j\) 为横坐标(\(x\)),\(f_j\) 为纵坐标(\(y\))的平面直角坐标系当中,这是一条以 \(S+t_i\) 为斜率(\(k\)),以 \(f_i-c_i\times t_i-S\times c_n\) 为截距(\(b\))的直线(\(y=kx+b\))。因此每一个候选的决策都是一个坐标系中的点,即每一个 \(j\) 都对应着一个点 \((c_j,f_j)\),而我们要求的 \(f_i\) 对应每一个点对应直线的截距,每个直线的斜率是固定的,而截距是未知的。综上所述,当截距最小时,\(f_i\) 也最小。
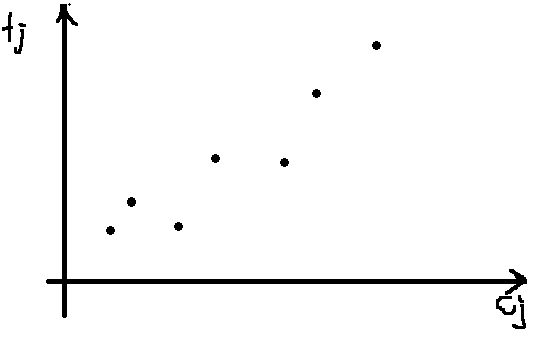
对于三个决策点 \((c_{j_1},f_{j_1})\),\((c_{j_2},f_{j_2})\),\((c_{j_3},f_{j_3})\),设 \(j_1<j_2<j_3\),因为 \(T,C\) 都是正整数所以 \(t\) 和 \(c\) 都有单调性。
探究什么情况时,\(j_2\) 有可能是最优决策:
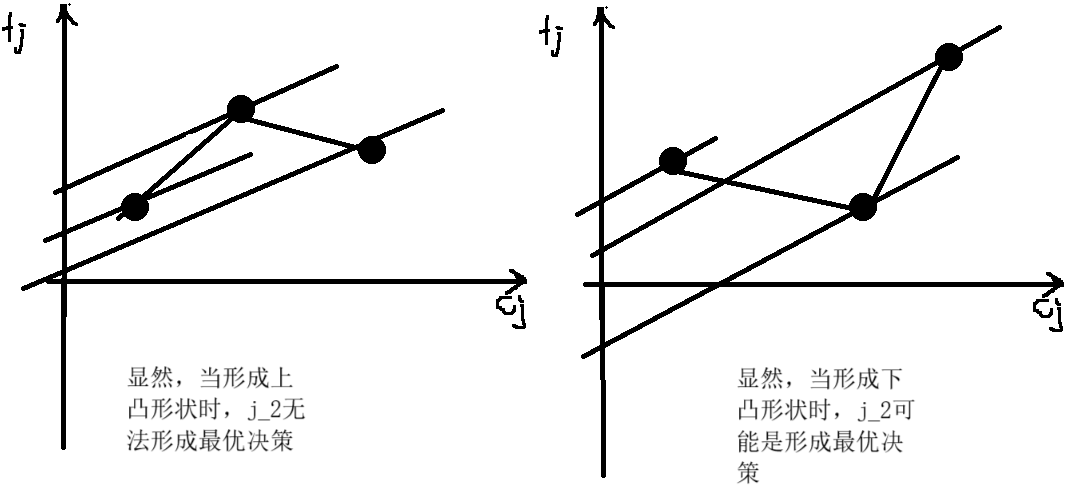
如上图所示,\(j_2\) 有可能是最优决策,当且仅当:
上示的不等式实际上是连接两个决策点连线的斜率,通俗的讲,我们应该维护“链接相邻两点的线段斜率”单调递增的一个“下凸壳”,只有这个下凸壳的顶点才有可能成为最优决策。实际上,对于一条斜率为 \(k\) 的直线,若某个点的左侧线段比 \(k\) 小、右侧线段的斜率比 \(k\) 大,则该顶点就是最优决策。换言之,如果把这条直线和所有线段组成一个排列组成一个序列,那么令结局最小化的定点就出现在按照斜率大小排序时,直线应该排在的位置上。
在本题中,\(j\) 的范围是 \(0\le j<i\),随着 \(i\) 的增大 ,都会有一个新决策出现。因为 \(c\) 的单调性,新决策的单调性一定会大于之前所有决策点的单调性。由于 \(t\) 的单调性,每次的斜率 \(S+t_i\) 也单调递增,如果每次只保留“相邻两点的线段斜率”大于 \(S+t_i\) 的部分,那凸壳的最左端点就一定是最优决策。
综上,对于代码操作,我们建立一个单调队列 \(q\),维护这个下凸壳。
对于每个决策 \(i\):
-
检查队头决策 \(q_l\) 和 \(q_{l+1}\),若斜率 $(f_{q_{l+1}}-f_{q_l})/(c_{q_{l+1}}-c_{q_l})\le S+t_i $,则 \(q_l\) 出队,检查新对头。
-
取队头 \(q_l\) 为最优决策,计算 \(f_i\)。
-
将新决策 \(i\) 队尾插入 ,插入前,若 \(q_r\) 不满足下凸性,即 \(q_r\) 是无用决策,就将 \(q_r\) 出队,检查新队尾。
时间复杂度 \(O(n)\)。