不定方程

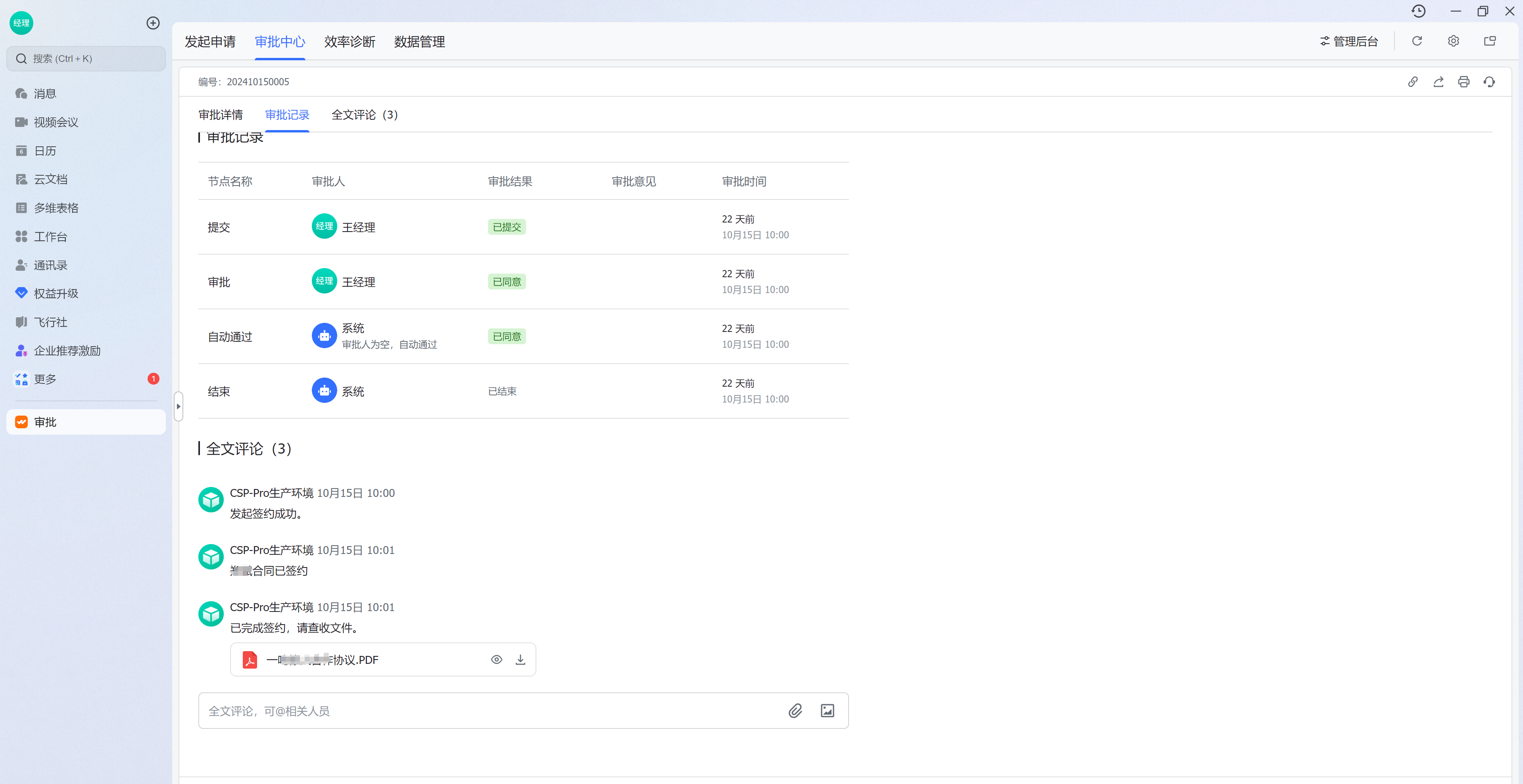
大佬们数竞学过的东西，这里来总结一下

（偷了一张教材来的）

0x00 一次不定方程（组）

根据未知数的次数可以给不定方程分类，其中最简单的便是一次不定方程了。这里和普通方程按照次数和未知数个数来分类的就不大一样了。

接下来来看定义。
设 \(k\ge 2\) 为整数，我们称方程

\[a_1x_1+a_2x_2+a_3x_3+\cdots+a_kx_k=c \]

为一次不定方程。其中 \(a_1，a_2，a_3，\cdots，a_k，c\) 都为整数，且 \(a_1，a_2，\cdots，a_k\) 都不为 \(0\)。并非每个一次不定方程都会有整数解。显然的必要条件就是

\[(a_1，a_2，a_3，\cdots，a_k)\mid c \]

我重点讨论的，是两个参数的一次不定方程，形如

\[ax+by=c \]

其中每个参数都符合上述要求。

接下来看一些定理。

定理1：不定方程 \(ax+by=c\) 有整数解的充分条件是 \(（a，b）\mid c\)。

证明没啥好说的。

定理2：设不定方程 \(ax+by=c\) 有整数解 \((x_0，y_0)\)，则 \(ax+by=c\) 的全部整数解为

\[\begin{cases}x=x_0+\dfrac{b}{(a，b)}t\\ \\y=y_0-\dfrac{a}{(a，b)}t \end{cases} \]

证明

设 \((x,y)\) 是 \(ax+by=c\) 的一组解，结合 \((x_0,y_0)\) 是 \(ax+by=c\) 的解，可知

\[\begin{cases}ax+by=c\\ ax_0+by_0=c\end{cases} \]

于是 \(a(x-x_0)+b(y-y_0)=0\)，

即 \(a(x-x_0)=b(y-y_0)\)，

故 \(b\mid a(x-x_0)\)，

因此 \(\dfrac{b}{(a,b)}\displaystyle\mid x-x_0\)，

可以设 \(x-x_0=\dfrac{b}{(a，b)}t\)

则 \(y-y_0=-\dfrac{a}{(a，b)}t\)，

哦对了其中 \(t\) 是整数哦。

因此定理2成立。