ARC191 192 题解

ARC191 题解

A - Replace Digits

简要题意

给定一个长为 \(n\) 的字符串 \(a\)。\(m\) 次操作，第 \(k\) 次给定一个字符 \(b_k\)，你需要选择一个 \(i \in [1, n]\) 并将 \(a_i\) 替换成 \(b_k\)。

求最后能得到的所有字符串中，字典序最大的是什么。

\(1 \leq n, m \leq 10^6\)，\(a_i, b_k\) 均为非零数字。

操作的顺序实际上没有太大关系，因此显然有一个贪心做法：从前往后依次考虑 \(a\) 的每一位，记此时 \(b\) 中还没用过的最大字符为 \(c\)，如果 \(c > a_i\) 就将 \(a_i\) 替换成 \(c\)。由于询问的是字典序，这么贪心显然是正确的。

不过虽然操作顺序没有太大关系，但它会带来一个特殊限制，即字符串 \(a\) 中至少有一个字符为 \(b_m\)。这个特判一下即可，如果最终 \(a\) 序列中没有任何一个字符为 \(b_m\)，那么就强制把 \(a_n\) 替换成 \(b_m\)。

时间复杂度为 \(\Theta(n + m)\) 或 \(\Theta(n + m \log m)\)，瓶颈在给 \(b\) 中的字符排序。

代码

#include <cstdio>
#include <queue>
#include <utility>
#define x first
#define y second
using namespace std;
const int N=(int)1e6+3;
int n,m; char a[N],b[N]; bool bj[N];
priority_queue<pair<char,int> > hp;
int main(){
//	freopen("digit.in","r",stdin);
//	freopen("digit.out","w",stdout);int i; bool ned=1;scanf("%d%d%s%s",&n,&m,&a[1],&b[1]);for(i=1;i<=m;i++) hp.emplace(b[i],i);for(i=1;i<=n&&!hp.empty();i++){if(hp.top().x<a[i]) continue;if(hp.top().y==m) ned=0;if(hp.top().x>a[i])a[i]=hp.top().x,bj[hp.top().y]=1,hp.pop();}if(ned) a[n]=b[m];puts(&a[1]);
//	fclose(stdin);
//	fclose(stdout);return 0;
}

B - XOR = MOD

简要题意

给定 \(n, m\)，称一个正整数 \(x\) 是“协调的”当且仅当 \(x \oplus n = x \bmod n\)，其中 \(\oplus\) 表示按位异或，\(\bmod\) 表示取模。

请你找出第 \(m\) 小的协调数，或报告不存在。

多测，\(1 \leq t \leq 2 \times 10^5\)，\(1 \leq n, m \leq 10^9\)。

条件看起来很怪异，我们需要想办法把它转化成正常的表述。

首先，我们发现必有 \(x \geq n\)，否则 \(n = x \oplus (x \oplus n) = (x \bmod n) \oplus (x \oplus n) = 0\) 与题目矛盾。其次，根据取模的性质，有 \(0 \leq x \oplus n < n\)，这告诉我们在二进制下，\(x\) 与 \(n\) 位数相同。结合以上两点，我们可以推出 \(n \leq x < 2n\)，于是上述条件可以表示为 \(x \oplus n = x - n\)。

我们知道，异或相当于不进位的加法、不退位的减法，而这两个数进行减法无论退不退位得出的结果都是一样的，这告诉我们相减的过程中不存在退位，即 \(n\) 为 \(1\) 的位 \(x\) 也必须为 \(1\)。结合上面的结论 \(x\) 与 \(n\) 位数相同，手模一下即可发现这两个条件是充要的。于是题目转化为：

首先将 \(n\) 转化为一个不含前导 \(0\) 的二进制数，你可以选择其中一些值为 \(0\) 的数位并替换为 \(1\)（也可以不选），求所有方案中得到的第 \(m\) 小的二进制数。

于是问题就简单了。设 \(n\) 的二进制表示中有 \(p\) 个 \(0\)，只需将 \(m - 1\) 转化为一个 \(p\) 位的二进制数，并依次填入值为 \(0\) 的数位即可。时间复杂度为 \(\Theta(T \log n)\)。

代码

#include <cstdio>
const int N=30;
int p,a[N];
int main(){
//	freopen("compatible.in","r",stdin);
//	freopen("compatible.out","w",stdout);int i,t,n,m;for(scanf("%d",&t);t>0;t--){scanf("%d%d",&n,&m),m--,p=0;for(i=0;(1<<i)<=n;i++)if(!(n>>i&1)) a[p++]=i;if(m>=(1<<p)) puts("-1");else{for(i=0;i<p;i++)if(m>>i&1) n|=1<<a[i];printf("%d\n",n);}}
//	fclose(stdin);
//	fclose(stdout);return 0;
}

C - A^n - 1

简要题意

给定正整数 \(n\)，你需要构造两个正整数 \(a, m\)，满足 \(1 \leq a, m \leq 10^{18}\)，且 \(n\) 是 \(a\) 在模 \(m\) 意义下的阶。

多测，\(1 \leq t \leq 10^4\)，\(1 \leq n \leq 10^9\)。

感觉这种题完全不是人能想到的啊……

首先你需要写一个暴力，随便构造一个满足 \(n \mid \varphi(m)\) 的正整数 \(m\)，然后类似于求原根的过程，从小到大枚举每个 \(a\) 是否合法。然后这个程序连样例都跑不动，但你惊讶地发现：

\({(n + 1)}^n \equiv 1 \pmod {n^2}\)	\({(n + 1)}^{n^2} \equiv 1 \pmod {n^3}\)	\({(n + 1)}^{n^3} \equiv 1 \pmod {n^4}\)	\({(n + 1)}^{n^4} \equiv 1 \pmod {n^5}\)	\({(n + 1)}^{n^5} \equiv 1 \pmod {n^6}\)
\(3^2 \equiv 1 \pmod 4\)	\(3^4 \equiv 1 \pmod 8\)	\(3^8 \equiv 1 \pmod {16}\)	\(3^{16} \equiv 1 \pmod {32}\)	\(3^{32} \equiv 1 \pmod {64}\)
\(4^3 \equiv 1 \pmod 9\)	\(4^9 \equiv 1 \pmod {27}\)	\(4^{27} \equiv 1 \pmod {81}\)	\(4^{81} \equiv 1 \pmod {243}\)	\(4^{243} \equiv 1 \pmod {729}\)
\(6^5 \equiv 1 \pmod {25}\)	\(6^{25} \equiv 1 \pmod {125}\)	\(6^{125} \equiv 1 \pmod {625}\)	\(6^{625} \equiv 1 \pmod {3125}\)	\(6^{3125} \equiv 1 \pmod {15625}\)

直接把 \(a = n + 1, m = n^2\) 交上去便获得了 AC！

还是来想想这是为什么。事实上，由二项式定理，有

\[(n + 1)^x = \sum_{k = 0}^x \binom{x}{k} n^k = 1 + \binom{x}{1} n + n^2 \sum_{k = 2}^x \binom{x}{k} n^{k - 2} \equiv nx + 1 \pmod{n^2} \]

代码

#include <cstdio>
int main(){
//	freopen("constraint.in","r",stdin);
//	freopen("constraint.out","w",stdout);int t,n;for(scanf("%d",&t);t>0;t--){scanf("%d",&n);printf("%d %lld\n",n+1,(long long)n*n);}
//	fclose(stdin);
//	fclose(stdout);return 0;
}

D - Moving Pieces on Graph

简要题意

给定一张 \(n\) 个点 \(m\) 条边的简单无向连通图，点和边均从 \(1\) 开始编号。有两枚棋子 A 和 B，初始时分别在点 \(S\) 和 \(T\)。

你可以进行任意多次操作，每次操作你可以选择一枚棋子，并将其移动到与之相邻的某个结点上。你的目标是将 A 移动到 \(T\)、将 B 移动到 \(S\)，你需要求出达到目标的最小操作次数。如果无解，输出 \(-1\)。

\(2 \leq n \leq 2 \times 10^5\)，\(n - 1 \leq m \leq \min\{\frac{n(n - 1)}{2}, 2 \times 10^5\}\)，\(S \neq T\)。

首先发现如果 \(S\) 到 \(T\) 的最短路径上（不包括 \(S, T\)）存在度数大于等于 \(3\) 的点，那么答案至多为 \(2x + 2\)，其中 \(x\) 是最短路径的长度。具体构造方法为：记该点为 \(P\)，那么 \(P\) 一定连向了某个最短路之外的点 \(Q\)，于是先将 A 沿最短路径移到 \(P\) 再移到 \(Q\)，再将 B 沿最短路径从 \(T\) 移到 \(S\)，最后将 A 移回 \(P\) 再沿最短路径移到 \(T\)。此时总共经过了两遍最短路径外加 \(PQ\) 这条边两次，总共走了 \(2x + 2\) 步。

由最短路径的性质，显然答案至少为 \(2x\)。于是我们只需要关心最短路上存在度数至少为 \(3\) 的点时，答案是否可能为 \(2x\) 或 \(2x + 1\)。这个只需求一遍非严格次短路，判断次短路的长度是否为 \(x\) 或 \(x + 1\)，容易发现此时求出的次短路必然至少有一个点不在最短路上。事实上这种做法不仅限于“最短路上存在度数至少为 \(3\) 的点”这个条件，只要求出的次短路长度不超过 \(x + 1\) 都是合法的。这种情况下问题就解决了。

现在剩下的情况为：最短路上除端点外所有点度数均为 \(2\)，且次短路的长度至少为 \(n - 2\)。此时最短路相当于从 \(S\) 到 \(T\) 的一条链，且除端点外链上的每个点都不与链外的点相连。因此一枚棋子的移动方案要么包含整条最短路径，要么与最短路径只在端点处相交。由调整法可知，A 和 B 中至少有一枚棋子的移动方案包含最短路径。不妨令这枚棋子是 A，那么答案有以下两种可能：

• B 的移动方案与最短路径只在端点处相交。那么 A 的移动路径恰为刚才求出的最短路径，B 的移动路径为将整个图扣去刚才求出的最短路径上的边后，剩余图的最短路径。记对 B 求出的最短路径长度为 \(y\)，此时答案为 \(x + y\)。

• B 的移动方案也包含最短路径。根据上面的性质，显然对于任意时刻，A 和 B 同时在非端点的最短路径上是不优的。那么最优方案一定形如：

  • 找到一个度数至少为 \(3\) 的点 \(P'\)，记 \(S\) 到 \(P\) 的某条路径为 \(l\)，记 \(E, F\) 为两个不在 \(l\) 上且与 \(P\) 相邻的结点。
  • 将 A 沿 \(l\) 走到 \(P\)，再沿边走到 \(E\)。
  • 将 B 沿最短路径走到 \(S\)，再沿 \(l\) 走到 \(P\)，然后沿边走到 \(F\)。
  • 将 A 沿边走到 \(P\)，再沿 \(l\) 走到 \(S\)，最后沿最短路径走到 \(T\)。
  • 将 B 沿边走到 \(P\)，再沿 \(l\) 走到 \(S\)。

  在上述过程中把 A 和 B、\(S\) 和 \(T\) 交换也可以。记路径 \(l\) 的长度为 \(z\)，此时答案为 \(2x + 4z + 4\)。我们只需要求出 \(z\) 的最小值，这个只需要求一遍从 \(S\) 或 \(T\) 出发到每个点的最短路，然后枚举每个度数至少为 \(3\) 的点，求出这些点的最短距离的最小值即可。

根据上面的情况分类讨论即可。由于边权均为 \(1\)，求最短路和次短路均可以使用 bfs 实现，时间复杂度为 \(\Theta(n + m)\)。

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <queue>
#define x first
#define y second
using namespace std;
const int N=200003;
int n,m,deg[N],dis1[N][2],dis2[N],pre[N],la[N];
int len_list=0,e[N*2],ne[N*2],h[N]; bool ban[N*2];
void add_once(int a,int b){e[len_list]=b;ne[len_list]=h[a];h[a]=len_list++;
}
void add_twice(int a,int b){add_once(a,b);add_once(b,a);
}
void bfs1(int S){int i,s1; bool s2;queue<pair<int,bool> > dl;dis1[S][0]=0,dl.emplace(S,0);while(!dl.empty()){s1=dl.front().x,s2=dl.front().y,dl.pop();for(i=h[s1];i>=0;i=ne[i])if(dis1[e[i]][0]==-1){dis1[e[i]][0]=dis1[s1][s2]+1;dl.emplace(e[i],0);pre[e[i]]=s1,la[e[i]]=i;}else if(dis1[e[i]][1]==-1){dis1[e[i]][1]=dis1[s1][s2]+1;dl.emplace(e[i],1);}}
}
void bfs2(int S){int i,s1; queue<int> dl;dis2[S]=0,dl.push(S);while(!dl.empty()){s1=dl.front(),dl.pop();for(i=h[s1];i>=0;i=ne[i])if(!ban[i]&&dis2[e[i]]==-1){dis2[e[i]]=dis2[s1]+1;dl.push(e[i]);}}
}
int main(){
//	freopen("graph.in","r",stdin);
//	freopen("graph.out","w",stdout);int i,x,y,S,T,ans1,ans2=-1;scanf("%d%d%d%d",&n,&m,&S,&T);memset(h,-1,sizeof h);for(i=1;i<=m;i++){scanf("%d%d",&x,&y);add_twice(x,y);deg[x]++,deg[y]++;}memset(dis1,-1,sizeof dis1),bfs1(S);if(dis1[T][1]==-1){puts("-1"); return 0;}if(dis1[T][1]<dis1[T][0]+2){printf("%d\n",dis1[T][0]+dis1[T][1]); return 0;}for(i=pre[T];i!=S;i=pre[i])if(deg[i]>2) break;if(i!=S){printf("%d\n",dis1[T][0]*2+2); return 0;}for(i=T;i!=S;i=pre[i]) ban[la[i]]=ban[la[i]^1]=1;memset(dis2,-1,sizeof dis2),bfs2(S);ans1=(dis2[T]==-1)?-1:(dis1[T][0]+dis2[T]);for(i=1;i<=n;i++)if(dis2[i]>=0&&deg[i]>=3)ans2=(ans2==-1)?dis2[i]:min(ans2,dis2[i]);memset(dis2,-1,sizeof dis2),bfs2(T);for(i=1;i<=n;i++)if(dis2[i]>=0&&deg[i]>=3)ans2=(ans2==-1)?dis2[i]:min(ans2,dis2[i]);if(ans2>=0) ans2=ans2*4+dis1[T][0]*2+4;if(ans1>=0&&ans2>=0) printf("%d\n",min(ans1,ans2));else printf("%d",max(ans1,ans2));
//	fclose(stdin);
//	fclose(stdout);return 0;
}

E - Unfair Game

简要题意

有 \(n\) 个袋子，第 \(i\) 个袋子里面装有 \(a_i\) 个金币和 \(b_i\) 个银币。另外给定两个参数 \(x, y\)。

甲和乙两人正在用这 \(n\) 个袋子玩游戏。初始时，你会从中挑选一些袋子分配给甲（可以不选，也可以全部选完），并将剩余的袋子分配给乙。然后从甲开始，两人轮流执行以下过程：

• 当前玩家从他拥有的袋子中选取一个，袋子中至少要装有一枚硬币。然后从以下两个操作中选择恰好一个操作来执行：
  • 从袋子中扔掉一枚金币，并向袋子中加入若干银币。加入银币的数量为：如果当前玩家是甲就加入 \(x\) 枚，否则加入 \(y\) 枚。这个操作能够执行当且仅当该袋子中有至少一枚金币。
  • 从袋子中扔掉一枚银币。这个操作能够执行当且仅当该袋子中有至少一枚银币。
• 然后，将这个袋子递给另一名玩家。

无法继续进行操作的人失败，另一个人胜利。

你需要求出初始时有多少种分配袋子的方案，使得最终甲能够获胜。答案对 \(998244353\) 取模。

\(1 \leq n \leq 2 \times 10^5\)，\(1 \leq x, y \leq 10^9\)，\(0 \leq a_i, b_i \leq 10^9\)。

先考虑只有一个袋子的时候怎么办。此时问题可以拓展为：给定 \(x, y, a, b\)，判断甲先手和乙先手两种情况到底谁胜利。手模一下即可发现，由于操作轮流进行且 \(x \neq y\)，最后谁胜只和奇偶性以及哪方先手有关。不难发现这又需要分类讨论，先从最简单的情况入手。

• 如果 \(x, y\) 均为奇数，那么银币数量的奇偶性不发生变化。因此如果 \(b\) 是奇数那么先手必胜，否则后手必胜。
• 如果 \(x, y\) 均为偶数，那么硬币总数的奇偶性不发生变化。因此如果 \(a + b\) 是奇数那么先手必胜，否则后手必胜。
• 如果 \(x\) 为奇数、\(y\) 为偶数，此时哪方必胜看起来难以判断。不妨从更小的情况开始判断。
  • 如果 \(a = 0\)，显然 \(b\) 是奇数时先手必胜，\(b\) 为偶数时后手必胜。
  • 如果 \(a = 1\)，此时乙操作金币会改变银币数量的奇偶性，而甲不会。感觉依然难以判断，不妨按哪方先手和 \(b\) 的奇偶性继续判断。
    • 甲先手且 \(b\) 为奇数。此时甲只需在第一次操作中去掉金币、加入 \(x\) 枚银币，使银币数量变成偶数。后面每次轮到甲时必然还有奇数枚银币，因此甲永远可以操作，最后甲必胜。
    • 甲先手且 \(b\) 为偶数。与上面相反，此时甲只能操作银币，否则他必输。轮到乙时有奇数枚银币，乙的策略为：始终操作银币。这样递归下去，每次轮到甲时都有偶数枚银币，甲只能操作银币，因为一旦把操作金币的机会用掉后面就必输；每次轮到乙时都有奇数枚银币，因此乙永远可以操作银币。若乙始终会操作银币，最后第一个无法操作银币的人是甲，此时甲只能操作金币，然后双方轮流操作银币。由于 \(x\) 是奇数，轮到乙时必然有奇数枚银币，因此乙永远可以操作银币，最后乙必胜。
    • 乙先手且 \(b\) 为奇数。此时乙只需继续使用上一种情况的策略——每次都操作银币，就可以达到和上一种情况相同的过程，最后乙必胜。
    • 乙先手且 \(b\) 为偶数。由于乙操作金币会改变银币数量的奇偶性，乙只需在第一次操作时操作金币，后面轮到甲时必然还剩偶数枚银币，轮到乙时还剩奇数枚，最后乙必胜。
  • 总结一下，\(b\) 为奇数时先手必胜，\(b\) 为偶数时乙必胜。
  • 如果 \(a \geq 2\)，受上述分讨的启发，由于乙操作金币会改变银币数量的奇偶性，而甲不会，因此乙的策略为：第一次操作时判断此时银币数量的奇偶性，若为奇数则操作银币，否则操作金币；此后一直操作银币。因此轮到乙时必然还剩奇数枚金币，乙永远可以操作，最后乙必胜。
• 如果 \(x\) 为偶数、\(y\) 为奇数，那么甲乙的状态与上面相反，先后手的状态不变，有：
  • 如果 \(a = 0\)，那么 \(b\) 是奇数时先手必胜，\(b\) 为偶数时后手必胜。
  • 如果 \(a = 1\)，那么 \(b\) 为奇数时先手必胜，\(b\) 为偶数时甲必胜。
  • 如果 \(a \geq 2\)，那么甲必胜。

---

上面是只有一个袋子的情况，可事实上有很多袋子，怎么办呢？事实上，可以发现一个袋子只有在被操作的时候它的主人才会变，因此每个袋子本质上是独立的。在题目给定的条件下，根据上面的方法，我们可以对每一个袋子求出在每一方先手的时候，哪一方会胜利。

显然对于一种方案，我们可以调整操作的顺序，使得对同一个袋子的操作被调整到一起。这本质上相当于：对每一个袋子而言，先手胜利相当于下一个袋子的先手转交给另一方，先手失败相当于下一个袋子的先手仍然是当前这一方。因此对于最初的一种分配方案，最终甲胜利等价于：“属于甲的先手胜利的袋子数量”严格大于“属于乙的先手胜利的袋子数量”。

记一个变量 \(x\) 表示“属于甲的先手胜利的袋子数量”减去“属于乙的先手胜利的袋子数量”，对每一个袋子决策它是分配给甲还是分配给乙。可以依据上面的数据求出，若分配给甲则对 \(x\) 有 \(+1 / 0\) 的贡献，若分配给乙则对 \(x\) 有 \(-1 / 0\) 的贡献。最终甲胜利等价于 \(x > 0\)。考虑贪心，先默认考虑贡献较少的那种选择，再将某些袋子调整至贡献较多的那种选择。记调整前的 \(x\) 值为 \(-\mathrm{sum}\)，那么调整后需要至少增加 \(\mathrm{sum} + 1\) 的贡献甲才能胜利。

此时所有袋子可以划分成三类：调整后贡献增加 \(0 / 1 / 2\)。显然第一类袋子是无关紧要的，记这类袋子的数量为 \(\Delta\)，那么再去掉这一类袋子后对后两类袋子计数，算出的答案再乘上 \(2^\Delta\) 即可。剩下的问题就是对后两类袋子进行计数，考虑双重循环，第一重枚举最终贡献的增加量，第二重枚举第三类袋子的数量，此时可以自然求出第一类袋子的数量，因此内部直接用组合数计数即可。这样我们就得到了一个 \(\Theta(n^2)\) 的算法。

代码（$\Theta(n^2)$）

#include <cstdio>
#include <iostream>
using namespace std;
const int N=200003,mod=998244353;
int fact[N],finv[N];
int pow(int a,int b){int ans=1;while(b>0){if(b&1) ans=(long long)ans*a%mod;a=(long long)a*a%mod; b>>=1;}return ans;
}
void init_fact(int n){fact[0]=1;for(int i=1;i<=n;i++)fact[i]=(long long)fact[i-1]*i%mod;finv[n]=pow(fact[n],mod-2);for(int i=n-1;i>=0;i--)finv[i]=(long long)finv[i+1]*(i+1)%mod;
}
int C(int a,int b){if(a<0||b<0||b>a) return 0;return (long long)fact[a]*finv[b]%mod*finv[a-b]%mod;
}
int main(){
//	freopen("game.in","r",stdin);
//	freopen("game.out","w",stdout);int i,j,x,y,s1,s2,n,cnt1=0,cnt2=0,lft=1,add=0,ans=0;scanf("%d%d%d",&n,&x,&y),init_fact(n);for(i=1;i<=n;i++){scanf("%d%d",&s1,&s2); bool s3,s4;if((x&1)==(y&1)) s3=s4=(x&1)?(s2&1):(s1+s2&1);else if(!s1) s3=s4=(s2&1);else if(s1>1) s3=!(x&1),s4=!(y&1);else s3=!(x&1)||(s2&1),s4=!(y&1)||(s2&1);add+=s4,(s3!=s4)?(cnt1++):(cnt2+=s3);if(!s3&&!s4) lft=lft*2%mod;}for(i=add+1;i<=cnt1+cnt2*2;i++){s1=max((i-cnt1+1)/2,0),s2=min(i/2,cnt2);for(j=s1;j<=s2;j++) ans=(ans+(long long)C(cnt2,j)*C(cnt1,i-j*2)%mod)%mod;}printf("%lld",(long long)ans*lft%mod);
//	fclose(stdin);
//	fclose(stdout);return 0;
}

考虑优化。观察上面的代码，我们发现第一个组合数只与 \(j\) 有关，第二个组合数同时与 \(i, j\) 有关，因此我们不妨交换循环顺序，将 \(j\) 提到最外层，将第一个组合数提到第一层循环进行计算。此时第二层循环内就只剩下了一个组合数，由于上标是个定值，因此我们只需进行前缀和优化即可。

时间复杂度为 \(\Theta(n)\)。

代码（$\Theta(n)$）

#include <cstdio>
#include <iostream>
using namespace std;
const int N=200003,mod=998244353;
int fact[N],finv[N],sumC[N];
int pow(int a,int b){int ans=1;while(b>0){if(b&1) ans=(long long)ans*a%mod;a=(long long)a*a%mod; b>>=1;}return ans;
}
void init_fact(int n){fact[0]=1;for(int i=1;i<=n;i++)fact[i]=(long long)fact[i-1]*i%mod;finv[n]=pow(fact[n],mod-2);for(int i=n-1;i>=0;i--)finv[i]=(long long)finv[i+1]*(i+1)%mod;
}
int C(int a,int b){if(a<0||b<0||b>a) return 0;return (long long)fact[a]*finv[b]%mod*finv[a-b]%mod;
}
int main(){
//	freopen("game.in","r",stdin);
//	freopen("game.out","w",stdout);int i,x,y,s1,s2,n,cnt1=0,cnt2=0,lft=1,add=0,ans=0;scanf("%d%d%d",&n,&x,&y),init_fact(n);for(i=1;i<=n;i++){scanf("%d%d",&s1,&s2); bool s3,s4;if((x&1)==(y&1)) s3=s4=(x&1)?(s2&1):(s1+s2&1);else if(!s1) s3=s4=(s2&1);else if(s1>1) s3=!(x&1),s4=!(y&1);else s3=!(x&1)||(s2&1),s4=!(y&1)||(s2&1);add+=s4,(s3!=s4)?(cnt1++):(cnt2+=s3);if(!s3&&!s4) lft=lft*2%mod;}for(i=1,sumC[0]=1;i<=cnt1;i++)sumC[i]=(sumC[i-1]+C(cnt1,i))%mod;for(i=0;i<=cnt2;i++){if(cnt1+i*2<=add) continue;s1=(sumC[cnt1]-((add<i*2)?0:sumC[add-i*2])+mod)%mod;ans=(ans+(long long)C(cnt2,i)*s1%mod)%mod;}printf("%lld",(long long)ans*lft%mod);
//	fclose(stdin);
//	fclose(stdout);return 0;
}

ARC192 题解

A - ARC arc

简要题意

对于长度为 \(n\) 的 0-1 序列 \(a\) 和长度也为 \(n\)、且由大写字母构成的字符串 \(S\)（下标均从 \(1\) 开始），你可以基于 \(S\) 对序列 \(a\) 做任意多次以下操作，包括 \(0\) 次：

• 选择一个下标 \(i \in [1, n]\)，满足 \(S_i = \texttt{A}, S_{i + 1} = \texttt{R}, S_{i + 2} = \texttt{C}\) 或 \(S_i = \texttt{C}, S_{i + 1} = \texttt{R}, S_{i + 2} = \texttt{A}\)，并将 \(a_{i}, a_{i + 1}\) 赋值为 \(1\)。

特殊地，我们规定 \(S_{n + 1}, S_{n + 2}, a_{n + 1}\) 分别表示 \(S_1, S_2, a_1\)。

现给定 \(n\) 和序列 \(a\)，求是否存在字符串 \(S\)，满足通过上述操作能够将 \(a\) 中的元素全部变成 \(1\)。

\(3 \leq n \leq 200000\)。

直接分类讨论即可。不妨令 \(a_n\) 和 \(a_1\) 是相邻的。

如果 \(4 \mid n\)，显然可以构造 \(S = \texttt{ARCR ARCR ARCR} \cdots\) 使得答案为 Yes。

如果 \(a\) 中存在相邻两位均为 \(1\)，不妨令 \(a_{n - 1} = a_n = 1\)。此时构造 \(S = \texttt{ARCR ARCR ARCR} \cdots\) 即可，答案为 Yes。

如果 \(a\) 中的数全为 \(0\)，为了使 \(a\) 中的数全都变为 \(1\)，每个位置都至少要被操作一次。符合条件的操作序列只可能为 \(S = \texttt{ARCR ARCR ARCR} \cdots\)，容易发现这种操作序列只会在 \(4 \mid n\) 的时候才会覆盖所有位置，因此答案为 Yes 当且仅当 \(4 \mid n\)。

---

否则一定可以将 \(a\) 划分成若干长度不小于 \(2\) 的段，每一段只有第一个元素为 \(1\)，其它元素均为 \(0\)。

先来考虑一个非常简单的情况：\(a\) 只能被划分成一段。不妨设 \(a_1 = 1\)，此时存在如下构造方法：

• 如果 \(n \bmod 4 = 0\)，那么有 \(S = \texttt{ARCR ARCR ARCR} \cdots \texttt{ARCR}\) 或 \(\texttt{CRAR CRAR CRAR} \cdots \texttt{CRAR}\)。
• 如果 \(n \bmod 4 = 1\)，那么有 \(S = \texttt{A ARCR ARCR ARCR} \cdots \texttt{ARCR}\) 或 \(\texttt{C CRAR CRAR CRAR} \cdots \texttt{CRAR}\)。
• 如果 \(n \bmod 4 = 2\)，很遗憾，没有符合条件的字符串 \(S\)。
• 如果 \(n \bmod 4 = 3\)，那么有 \(S = \texttt{C ARCR ARCR ARCR} \cdots \texttt{ARCR AR}\) 或 \(\texttt{A CRAR CRAR} \cdots \texttt{CRAR CR}\)。

将其拓展一下，我们发现：只要 \(n \bmod 4 \neq 2\)，那么答案一定为 Yes，将上面的构造方法照搬过来即可。

事实上当 \(n \bmod 4 = 2\) 时，如果存在长度为奇数的段也有解。不妨令 \(a_1 1\) 且 \(a_1\) 所在的段 \([1, x]\) 长度为奇数，那么只需要将 \([1, x]\) 和 \([x + 1, n]\) 这两个区间分别采用上面的方法构造。由于两个区间的长度除以 \(4\) 的余数相同，因此只需使它们的构造方法相同即可，答案为 Yes。

当 \(n \bmod 4 = 2\) 且所有段长度均为偶数时，由于同一段必然采用同一种构造方法，因此无论怎样划分区间，每个区间长度都一定是偶数。由于 \(n \bmod 4 \neq 0\)，因此必然有一个区间长度除以 \(4\) 余 \(2\)，因此答案为 No。

时间复杂度为 \(\Theta(n)\)。上面很多情况都可以合并。

代码

#include <cstdio>
const int N=200003;
int n,a[N];
int main(){
//	freopen("ARC.in","r",stdin);
//	freopen("ARC.out","w",stdout);int i,s1,cnt;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d",&a[i]);for(s1=0;s1<n;s1++)if(a[s1]) break;if(s1==n){puts((n%4==0)?"Yes":"No");return 0;}for(i=s1,cnt=1;i<=s1+n;i++)if(!a[i%n]) cnt++;else if(cnt&1) cnt=0;else break;puts((i<=s1+n||n%4==0)?"Yes":"No");
//	fclose(stdin);
//	fclose(stdout);return 0;
}

B - Fennec VS. Snuke 2

简要题意

给定长为 \(n\) 的序列 \(a\)，两人轮流进行如下操作：

• 选择下标 \(i \in [1, n]\) 满足 \(a_i > 0\)，并将 \(a_i\) 减去 \(1\)。

当所有元素都被操作过时，游戏立即结束，且进行最后一步操作的人胜利。请你判断先手是否必胜。

\(1 \leq n \leq 2 \times 10^5\)，\(1 \leq a_i \leq 10^9\)。

全场最困难的题。这种题必须从最简单的情况入手，模拟两人博弈的过程，并逐步扩展到更复杂的情况。

先说结论，在大部分情况下，先手必胜等价于 \(\sum a_i\) 为奇数。为什么呢？

不妨按照操作的顺序对元素进行重标号。首先我们知道，一旦第 \(n\) 个元素被操作，游戏立即结束，也就是说一旦一方操作了第 \(n - 1\) 个元素，那么另一方直接操作第 \(n\) 个元素即可获胜。因此双方都不希望操作第 \(n - 1\) 个位置，一旦已经操作过 \(n - 2\) 个元素，那么双方一定会轮流将这 \(n - 2\) 个元素都变成 \(0\)。此时双方都希望最后一次操作轮到自己，也就是说，先手希望这 \(n - 2\) 个元素的和为奇数，后手则希望它为偶数。

自然地，考虑将所有 \(a_i\) 按照初始的奇偶性分类。记 \(S_0\) 表示偶数元素构成的集合，\(S_1\) 表示奇数元素构成的集合。容易发现 \(|S_1|\) 与 \(\sum a_i\) 同奇偶性，且对博弈的过程来说，每一类中的元素都是本质相同的。

当 \(|S_1|\) 为偶数时，可以将 \(S_1\) 中的元素每两个分成一组。那么后手可以按如下策略进行操作：

• 如果上一轮先手操作的元素在之前就被操作过，那么后手继续操作这个元素。
• 否则，如果先手操作的元素属于 \(S_1\)，那么后手操作同一组的另外一个元素。
• 否则，如果此时 \(S_0\) 中仅剩一个元素还没操作，那么后手操作那个元素。
• 否则，后手继续操作上一轮先手操作的元素。

先尝试说明当 \(|S_0| > 1\) 时上面策略的合法性。容易归纳证明每一轮后手操作过后，当前状态都满足以下性质：

• 对于 \(S_1\) 中的每一组，这两个元素要么都被操作过，要么都没被操作过。
• \(S_0\) 中还没有被操作的元素数量要么不小于 \(2\)，要么等于 \(0\)。
• 对于已经被操作的元素，它们当前的值一定为偶数。

根据性质 \(3\)，对于第一种情况，后手操作前，上一轮先手操作过的元素必为奇数。因此所有操作总是合法的。根据性质 \(1\) 和 \(2\)，还没有被操作的元素个数要么不小于 \(2\)，要么为 \(0\)。因此最后一个元素一定是被后手操作的，即使用上述策略后，后手必胜。

当 \(|S_0|\) 为奇数时，先手先操作一个 \(S_1\) 中的元素，再将剩余的元素分组。剩下的流程与上述情况同理，将先后手交换一下即可。因此此时先手必胜。

综上，当 \(|S_0| > 1\) 时，先手必胜等价于 \(|S_1|\) 为奇数，即 \(\sum a_i\) 为奇数。

将剩余的边界特判一下即可通过本题。时间复杂度为 \(\Theta(n)\)。

代码

#include <cstdio>
int main(){
//	freopen("optimal.in","r",stdin);
//	freopen("optimal.out","w",stdout);int i,n,cnt[2]={0},x;scanf("%d",&n);for(i=1;i<=n;i++)scanf("%d",&x),cnt[x&1]++;if(n<3) puts((n==1)?"Fennec":"Snuke");else if(!cnt[0]||!cnt[1]) puts((cnt[1]&1)?"Fennec":"Snuke");else if(cnt[0]==1&&cnt[1]==2) puts("Fennec");else puts((cnt[1]&1)?"Fennec":"Snuke");
//	fclose(stdin);
//	fclose(stdout);return 0;
}

C - Range Sums 2

简要题意

这是一道交互题。

初始时，交互库会给你一个正整数 \(n\)。交互库有一个长为 \(n\) 的排列 \(p\) 和一个长为 \(n\) 的序列 \(a\)，并且满足 \(p_1 < p_2\)。

你可以向交互库提问。每次询问，你需要给定两个正整数 \(s, t\)，满足 \(1 \leq s, t \leq n\) 且 \(s \neq t\)。交互库会返回

\[\sum_{i = \min\{p_s, p_t\}}^{\max\{p_s, p_t\}} a_i \]

你需要通过不超过 \(2n\) 次操作求出 \(p\) 和 \(a\)。

\(3 \leq n \leq 5000\)，\(1 \leq a_i \leq 10^9\)。

记 \(S(l, r)\) 表示 \(\sum_{i = l}^r a_i\)，\(S(r) = \sum_{i = 1}^r a_i\)，那么一次询问 \((s, t)\) 返回的值为 \(S(\min\{p_s, p_t\}, \max\{p_s, p_t\})\)。

考虑我们能够通过询问得到什么。对于三个下标 \(i, j, k\)，进行三次询问 \((s = i, t = j), (s = j, t = k), (s = i, t = k)\)，那么我们能够推断出：

• \(p_i, p_j, p_k\) 的大小关系。不妨令 \((s = i, t = k)\) 在这三次询问中返回的值最大，则有 \(p_i < p_j < p_k\) 或 \(p_k < p_j < p_i\)。也就是说，如果之前已知 \(p_i, p_j, p_k\) 中任何两个元素间的大小关系，那么我们现在就能确定这三个元素间的大小关系。这里不妨假设 \(p_i < p_j < p_k\)。
• \(a_{p_j}\) 的值。三次询问分别返回 \(S(p_i, p_j), S(p_j, p_k), S(p_i, p_k)\)，那么有 \(a_{p_j} = S(p_i, p_j) + S(p_j, p_k) - S(p_i, p_k)\)。
• \(S(p_i - 1), S(p_j - 1), S(p_j), S(p_k)\) 间的数量关系。显然有 \(S(p_j - 1) - S(p_i - 1) = S(p_i, p_j) - a_{p_j}\)，\(S(p_j) - S(p_j - 1) = a_{p_j}\)，\(S(p_k) - S(p_j) = S(p_j, p_k) - a_{p_j}\)。

那么我们考虑维护序列 \(b_i\)：设立一个基准点 \(\mathrm{st}\)，对于下标 \(i < \mathrm{st}\) 维护 \(b_i = -S(p_i, \mathrm{st} - 1) = S(p_i - 1) - S(\mathrm{st} - 1)\)；对于下标 \(i > \mathrm{st}\)，维护 \(b_i = S(\mathrm{st} + 1, p_i) = S(p_i) - S(\mathrm{st})\)；特殊地，令 \(b_\mathrm{st} = 0\)。如果最终我们成功求出了序列 \(b\)，那么 \(p_i\) 间的大小关系即为 \(b_i\) 间的大小关系，我们也可以成功还原出排列 \(p\)；由于对 \(i < \mathrm{st}\) 有 \(a_{p_i} = b_{i + 1} - b_i\)，对 \(i > \mathrm{st}\) 有 \(a_{p_i} = b_i - b_{i - 1}\)，因此我们也可以几乎还原出序列 \(a\)。也就是说，我们需要

• 确定 \(\mathrm{st}\) 的值；
• 求出 \(a_{p_\mathrm{st}}\) 的值以及 \(b\) 序列。

接下来就简单了。首先进行三次询问 \((s = 1, t = 2), (s = 2, t = 3), (s = 1, t = 3)\)，那么 \(\mathrm{st}\) 可以设立为 \(p_1, p_2, p_3\) 的中位数，同时 \(a_{p_\mathrm{st}}\) 也就顺便求出来了。然后从左往右做扫描线，维护 \([1, i]\) 中 \(p\) 值最大的下标 \(l\)、\(p\) 值最小的下标 \(r\)、以及 \(S(p_l, p_r)\) 的值，更新的时候进行 \((s = l, t = i), (s = r, t = i)\) 两次询问，\(b\) 序列通过 \(S(x)\) 间的大小关系进行更新即可。

时间复杂度为 \(\Theta(n \log n)\)，总询问次数为 \(2n - 3\)。

代码

#include <algorithm>
#include <cstdio>
using namespace std;
const int N=5003;
int n,arr[N],res[N]; long long a[N],b[N];
long long ask(int s,int t){printf("? %d %d\n",s,t),fflush(stdout);long long x; scanf("%lld",&x); return x;
}
int main(){int i,lu,ru; long long st,s1,s2,s3,s4;scanf("%d",&n),s1=ask(1,2),s2=ask(1,3),s3=ask(2,3);if(s1>s2&&s1>s3)st=s2+s3-s1,a[3]=0,lu=1,ru=2,a[1]=-s2+st,a[2]=s3-st;else if(s2>s1&&s2>s3)st=s1+s3-s2,a[2]=0,lu=1,ru=3,a[1]=-s1+st,a[3]=s3-st;elsest=s1+s2-s3,a[1]=0,lu=3,ru=2,a[3]=-s2+st,a[2]=s1-st;for(i=4;i<=n;i++){s1=a[ru]-a[lu]+st,s2=ask(lu,i),s3=ask(ru,i);if(s1>s2&&s1>s3){s4=s2+s3-s1,s2-=s4,s3-=s4;a[i]=(s3<=a[ru])?(a[ru]-s3):(a[lu]+s2);}else if(s2>s1&&s2>s3)s4=s1+s3-s2,a[i]=a[ru]-s4+s3,ru=i;elses4=s1+s2-s3,a[i]=a[lu]+s4-s2,lu=i;}for(i=1;i<=n;i++) arr[i]=i;sort(arr+1,arr+n+1,[&](const int& u,const int& v){return a[u]<a[v];});putchar('!');for(i=1;i<=n;i++) res[arr[i]]=i;for(i=1;i<=n;i++) printf(" %d",res[i]);for(i=1;i<=n;i++)if(a[arr[i]]==0) printf(" %lld",st);else printf(" %lld",(a[arr[i]]>0)?(a[arr[i]]-a[arr[i-1]]):(a[arr[i+1]]-a[arr[i]]));putchar('\n'),fflush(stdout);return 0;
}

D - Fraction Line

简要题意

给定长为 \(n - 1\) 的序列 \(a_i\)（下标从 \(1\) 开始）。称一个长为 \(m\) 的序列 \(S\)（下标从 \(0\) 开始）是“好的”当且仅当：

• \(\gcd(S_0, S_1, S_2, \cdots, S_{m - 1}) = 1\)；
• 对 \(i \in [1, m - 1]\)，有 \(a_i = \dfrac{S_{i - 1}S_i}{\gcd^2(S_{i - 1}, S_i)}\)。

定义一个序列的权值为其所有元素的乘积。求所有长为 \(n\)的“好的”序列的权值之和，答案对 \(998244353\) 取模。

\(2 \leq n \leq 1000\)，\(1 \leq a_i \leq 1000\)。

容易发现关于每个质因数的限制是独立的，因此不妨将每个质因子分开考虑。最后使用乘法原理将每个质因子的答案乘起来即可。

令现在考虑质因子 \(p\)，求出 \(b_i\) 表示 \(a_i\) 分解质因数后，表达式中含有多少个质因子 \(p\)。此时一个好的序列 \(S_i\) 满足：

• 序列长度为 \(n\)，且每个元素均可以表示成 \(p^x (x \in N)\) 的形式。因此，令 \(x_i = \log_p S_i\)。
• \(x\) 中至少有一个元素为 \(0\)。
• 对于每个 \(i \in [1, n - 1]\)，要么 \(x_i = x_{i - 1} + b_i\)，要么 \(x_i = x_{i - 1} - b_i\)。

考虑 DP，设 \(f(i, j)\) 表示长为 \(i + 1\) 且 \(x_i = j\) 的所有“好的”序列的权值之和。那么有转移：

• 对于 \(x_i = x_{i - 1} + b_i\) 的序列，有 \(f(i + 1, j + b_i) \leftarrow f(i, j) \times p^{j + b_i}\)。
• 对于 \(x_i = x_{i - 1} - b_i\) 的序列，分以下两种情况：
  • 对于 \(j \geq b_i\)，有 \(f(i + 1, j - b_i) \leftarrow f(i, j) \times p^{j + b_i}\)。
  • 对于 \(j < b_i\)，则该序列对应到的新的“好的”序列为：保持原来的元素之间的差不变，将 \(x_i\) 增加至 \(j\)（并相应地改变前面的元素），并在 \(x\) 序列末尾增加元素 \(0\)。那么有转移 \(f(i + 1, 0) \leftarrow f(i, j) \times p^{(i + 1)(b_i - j)} \times p^0\)。

对于每个质因子，时间复杂度为 \(\Theta(n \sum b_i)\)。由于每个 \(a_i\) 最多含有不超过 \(9\) 个质因子，因此总时间复杂度为 \(\Theta(9n^2)\)。

代码

#include <cstdio>
#include <iostream>
using namespace std;
const int N=1003,M=9,mod=998244353;
int n,m,p,a[N],b[N],f[N*M],g[N*M],powp[N*M];
int len_prime=0,prime[N]; bool bj[N];
void get_prime(int n){int i,j; bj[1]=1;for(i=2;i<=n;i++){if(!bj[i]) prime[++len_prime]=i;for(j=1;j<=len_prime&&prime[j]*i<=n;j++){bj[prime[j]*i]=1;if(i%prime[j]==0) break;}}
}
int main(){
//	freopen("fraction.in","r",stdin);
//	freopen("fraction.out","w",stdout);int i,j,k,s1,ans=1;scanf("%d",&n);for(i=1;i<n;i++){scanf("%d",&a[i]);m=max(m,a[i]);}get_prime(m);for(i=1;i<=len_prime;i++){for(j=1,p=0;j<n;p=max(p,b[j]),j++)for(b[j]=0,k=a[j];k%prime[i]==0;k/=prime[i]) b[j]++;for(powp[0]=1,j=1;j<=p*n;j++)powp[j]=(long long)powp[j-1]*prime[i]%mod;for(j=1,p=0,f[0]=1;j<n;p+=b[j++]){for(k=0;k<=p;k++) g[k]=f[k];for(k=0;k<=p+b[j];k++) f[k]=0;for(k=0;k<=p;k++){if(!b[j]){ f[k]=(long long)g[k]*powp[k]%mod; continue; }f[k+b[j]]=(f[k+b[j]]+(long long)g[k]*powp[k+b[j]]%mod)%mod;if(k<b[j]) f[0]=(f[0]+(long long)g[k]*powp[(b[j]-k)*j]%mod)%mod;else f[k-b[j]]=(f[k-b[j]]+(long long)g[k]*powp[k-b[j]]%mod)%mod;}}for(j=0,s1=0;j<=p;j++) s1=(s1+f[j])%mod;ans=(long long)ans*s1%mod;}printf("%d",ans);
//	fclose(stdin);
//	fclose(stdout);return 0;
}

E - Snuke's Kyoto Trip

简要题意

现有一个平面直角坐标系，初始时每个整点都是白色的。给定 \(m, n, l, r, d, u\)，在坐标系上依次进行如下操作：

• 将以 \((0, 0)\) 为左下角、\((m, n)\) 为右上角的矩形（包括边界）包含的所有整点染黑。
• 将以 \((l, d)\) 为左下角、\((r, u)\) 为右上角的矩形（包括边界）包含的所有整点染白。

现在你可以从任意整点出发、在任意整点结束，每一步你可以向右或向上走一个单位长度，但是要求包括起点和终点在内，每个你经过的整点都必须是黑点。求满足条件的路径数量对 \(998244353\) 取模的值。

\(0 \leq l \leq r \leq m \leq 10^6\)，\(0 \leq d \leq u \leq n \leq 10^6\)。

只要你对组合数足够熟悉便可以秒掉这道题。首先，有公式

\[\sum_{i = l}^r \binom{q + i}{p} = \sum_{i = l}^r (\binom{q + i + 1}{p + 1} - \binom{q + i}{p + 1}) = \binom{q + r + 1}{p + 1} - \binom{q + l}{p + 1} \]

假设现有以 \((0, 0)\) 为左下角、以 \((m, n)\) 为右上角的矩形，你在矩形内移动，每一步可以向右或向上移动一个单位长度。考虑以下计数问题：

• 起点为 \((0, 0)\)、终点为 \((m, n)\) 的路径有多少条？这很简单，相当于在 \(m + n\) 步内任选 \(m\) 步向右走，其余 \(n\) 步向上走。答案即为

\[f_0(m, n) = \binom{m + n}{m} = \binom{m + n}{n} \]

• 起点为 \((0, 0)\)、终点任意的路径有多少条？枚举终点即可转化为上一个问题，答案即为

\[f_1(m, n) = \sum_{i = 0}^m \sum_{j = 0}^n \binom{i + j}{i} = \sum_{i = 0}^m (\binom{i + n + 1}{i + 1} - \binom{i}{i + 1}) = \sum_{i = 0}^m \binom{i + n + 1}{n} = \binom{m + n + 2}{n + 1} - \binom{n + 1}{n + 1} = \binom{m + n + 2}{m + 1} - 1 \]

• 起点任意、终点任意的路径有多少条？枚举起点即可转化为上一个问题，答案即为

\[\begin{align*} &f_2(m, n) = \sum_{i = 0}^m \sum_{j = 0}^n f_1(m - i, n - j) = \sum_{i = 0}^m \sum_{j = 0}^n f_1(i, j) \\ = &\sum_{i = 0}^m \sum_{j = 0}^n \binom{i + j + 2}{i + 1} - (m + 1)(n + 1) = \sum_{i = 0}^m (\binom{i + n + 3}{i + 2} - \binom{i + 2}{i + 2}) - (m + 1)(n + 1) \\ = &\sum_{i = 0}^m \binom{i + n + 3}{n + 1} - (m + 1)(n + 2) = \binom{m + n + 4}{n + 2} - \binom{n + 3}{n + 2} - (m + 1)(n + 2) = \binom{m + n + 4}{m + 2} - (m + 2)(n + 2) - 1 \end{align*} \]

预处理组合数后，上面的三个问题都可以 \(\Theta(1)\) 解决。于是剩下的问题就简单了。如图（1）所示，我们把能走的部分划分成红色和绿色两个 L 形，将路径分成三类：全在红色部分中、全在绿色部分中、横跨红色和绿色部分。

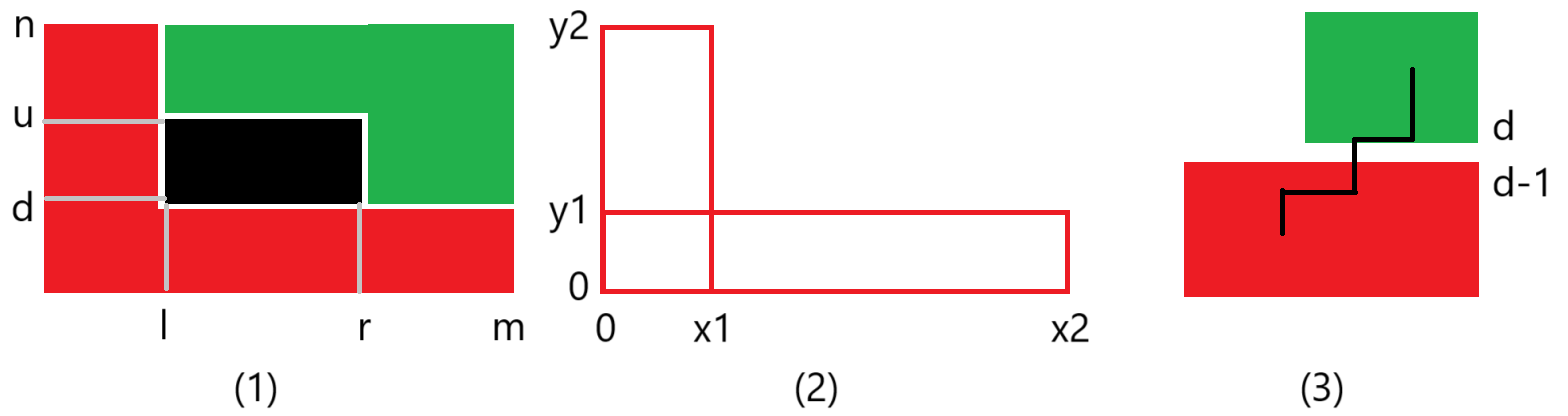
前两类路径都可以转化为 L 形区域内的路径计数，如图（2）所示。由上面的分析我们知道，矩形内的路径数量可以 \(\Theta(1)\) 求出，于是我们只需使用容斥原理把 L 型区域转化为矩形区域即可。一个 L 形区域内的路径数即为 \(f_2(x_1, y_2) + f_2(x_2, y_1) - f_2(x_1, y_1)\)。

第三类路径又可以分为两个小类，穿过右下角的分界线 和 穿过左上角的分界线，容易发现不存在同时属于两个小类的路径。我们以前者为例，沿着路径走的过程中，必然存在一步路既不属于红色部分也不属于绿色部分，且这步路是唯一的，如图（3）中纵坐标在 \(d - 1\) 和 \(d\) 之间的黑色线段所示。考虑枚举这步路，那么我们只需分别统计红色部分和绿色部分的路径数量即可。设这条线段为 \((i, d - 1) - (i, d)\)，那么红色部分相当于钦定终点为 \((i, d - 1)\)，绿色部分相当于钦定起点为 \((i, d)\)，经过这条线段的路径数即为 \(f_1(i, d - 1)f_1(m - i, n - d)\)。

时间复杂度为 \(\Theta(m + n)\)。

代码

#include <cstdio>
const int N=(int)2e6+10,mod=998244353;
int m,n,xl,xr,yl,yr,fact[N],finv[N];
int pow(int a,int b){int ans=1;while(b>0){if(b&1) ans=(long long)ans*a%mod;a=(long long)a*a%mod; b>>=1;}return ans;
}
void init_fact(int n){fact[0]=1;for(int i=1;i<=n;i++)fact[i]=(long long)fact[i-1]*i%mod;finv[n]=pow(fact[n],mod-2);for(int i=n-1;i>=0;i--)finv[i]=(long long)finv[i+1]*(i+1)%mod;
}
int C(int a,int b){if(a<0||b<0||b>a) return 0;return (long long)fact[a]*finv[b]%mod*finv[a-b]%mod;
}
int count1(int m,int n){return (C(m+n+2,n+1)+mod-1)%mod;
}
int count2(int m,int n){return ((C(m+n+4,n+2)-(long long)(m+2)*(n+2)%mod-1)%mod+mod)%mod;
}
int main(){
//	freopen("plane.in","r",stdin);
//	freopen("plane.out","w",stdout);int i,ans=0,s1,s2;scanf("%d%d%d%d%d%d",&m,&n,&xl,&xr,&yl,&yr),init_fact(m+n+4);s1=((count2(m,yl-1)+count2(xl-1,n)-count2(xl-1,yl-1))%mod+mod)%mod;s2=((count2(m-xl,n-yr-1)+count2(m-xr-1,n-yl)-count2(m-xr-1,n-yr-1))%mod+mod)%mod;for(i=xr+1;i<=m;i++)ans=(ans+(long long)count1(i,yl-1)*count1(m-i,n-yl)%mod)%mod;for(i=yr+1;i<=n;i++)ans=(ans+(long long)count1(xl-1,i)*count1(m-xl,n-i)%mod)%mod;ans=((long long)ans+s1+s2)%mod;printf("%d",ans);
//	fclose(stdin);
//	fclose(stdout);return 0;
}