利用极大似然估计计算概率
对于先验概率\(P(Y)\),似然函数为\(L=\underset{i=1}{\overset{m}{\prod}}P(Y=y_i)\),对数似然函数为\(l=\underset{i=1}{\overset{m}{\sum}}\log P(Y=y_i)\),注意到有约束条件\(\underset{k=1}{\overset{K}{\sum}}P(Y=c_k)=1\),于是利用拉格朗日乘数法可以得出下面的方程
\[\begin{cases}
\frac{\underset{i=1}{\overset{m}{\sum}}I(y_i=c_k)}{P(Y=c_k)}+\lambda=0 & k=1,2,...,K \\
\underset{k=1}{\overset{K}{\sum}}P(Y=c_k)=1
\end{cases}
\]
解这个方程组即可得出书上的公式
对于条件概率\(P(X|Y)\),似然函数为\(L=\underset{i=1}{\overset{m}{\prod}}P(X=x_i|Y=y_i)\),对数似然函数为\(l=\underset{i=1}{\overset{m}{\sum}}\log P(X=x_i|Y=y_i)\),注意到有约束条件\(\underset{s=1}{\overset{S}{\sum}}P(X=a_s|Y=c_k)=1,k=1,2,...,K\),于是利用拉格朗日乘数法可以得出下面的方程
\[\begin{cases}
\frac{\underset{i=1}{\overset{m}{\sum}}I(x_i=a_s,y_i=c_k)}{P(X=a_s|Y=c_k)}+\lambda_k=0 & k=1,2,...,K \\
\underset{s=1}{\overset{S}{\sum}}P(X=a_s|Y=c_k)=1 & k=1,2,...,K
\end{cases}
\]
于是可以得出书上的公式
注意在估计条件概率的时候,上面是假设特征是离散型的并且在\(Y\)给定后\(X\)符合多项式分布;如果特征是连续型的,一般就假设在\(Y\)给定后\(X\)符合高斯分布

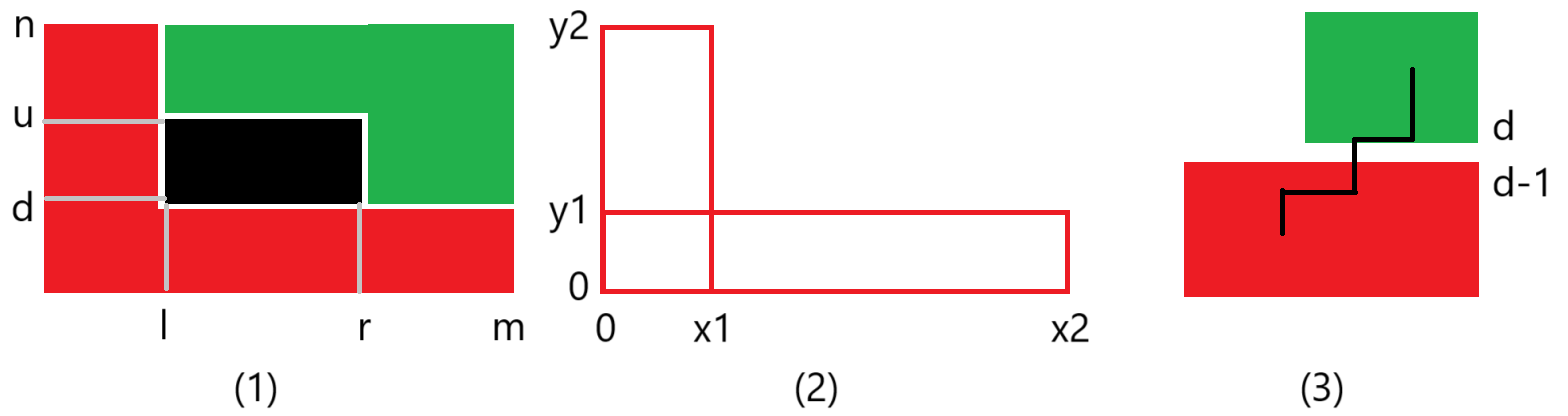

![P1083 [NOIP 2012 提高组] 借教室(差分)](https://img2024.cnblogs.com/blog/3599636/202502/3599636-20250211204308876-1856996136.png)
![P9330 [JOISC 2023] JOI 国的节日 2 题解](https://pic.imgdb.cn/item/64a1950f1ddac507cc802274.png)