【Deepseek】教你将Deepseek接入WPS和Word/Excel日常办公使用

以下文章来源于像梦又似花 ，作者小编

以下是将DeepSeek功能集成到WPS中的详细步骤，无需本地部署模型，直接通过官网连接使用：

1、下载并安装OfficeAI插件

（1）访问OfficeAI插件下载地址：https://www.office-ai.cn/，下载插件（目前只支持windows系统）。

OfficeAI 助手 是一款免费的智能AI办公工具软件，专为 Microsoft Office 和 WPS 用户打造。

【使用场景】：寻找如何输入"打勾（✔️）符号"的方法，想知道"怎么在插入表格前添加文字"，或者"该用哪个公式"， AI办公助手都能为你提供快速、准确的解决方案。 通过简单的指令，ExcelAI 插件可以帮你自动完成复杂的公式计算、函数选择。 WordAI 插件还具备整理周报、撰写会议纪要、总结内容、以及文案润色等功能。

同时，该插件支持文心一言、豆包、通义千问、deepseek等多个AI大模型引擎。

（2）下载完成后，双击安装文件，按照提示完成安装 。

2、 获取DeepSeek的API Key

（1）打开DeepSeek官网：

https://www.deepseek.com/

（2）点击右上角的"API开放平台"，登录账号（如果没有账号，可以先注册一个）。

（3）登录成功后，点击左侧的"API Keys"，然后点击"创建API Key"，输入一个名称，创建完成后复制生成的API Key。

3、配置OfficeAI插件

（1）OfficeAI插件安装完成后，打开WPS，此时在WPS界面中会多出一个"OfficeAI "的选项卡。

（2）点击"OfficeAI"选项卡，点击"设置"。

（3）在"设置"窗口中，选择"大模型设置"，打开"本地部署"开关，选择"ApiKey"标签。

在"大模型"下拉菜单中选择"Deepseek"，根据需求在"模型名"中选择deepseek-chat（DeepSeek-V3）或deepseek-reasoner（DeepSeek-R1)。

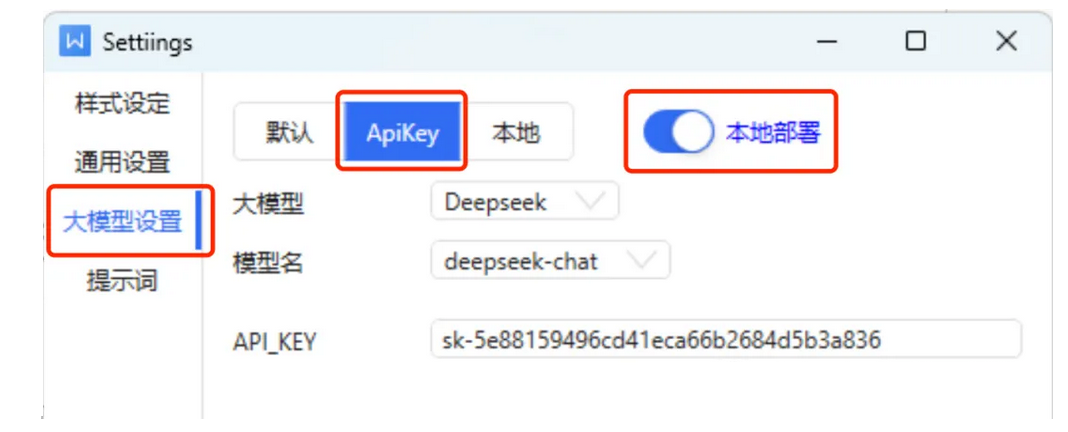
其中，chat模型适合普通的对话交流、搜索查询，reasoner适合深度思考、推理决策。可以先用chat模型试一下，如果发现满足不了需求，再打开设置改成reasoner模型。

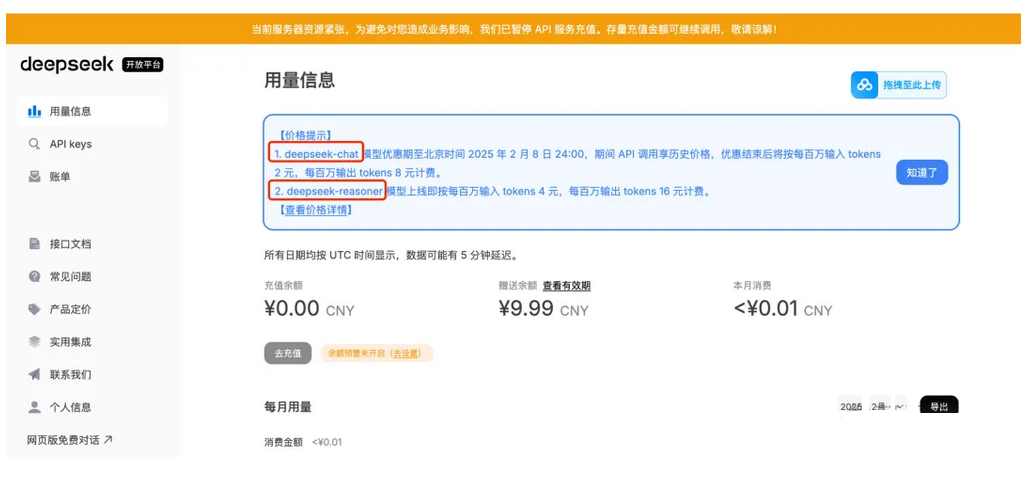
在deepseek官网上的用量信息页面，reasoner模型的价格是chat模型的两倍。deepseek会赠送10元的tokens，有效期为30天。

1个中文汉字约0.8-1个token，1个英文字母约0.3个token。也就是说，chat模型每输入1百万个汉字（你给deepseek发送的消息累计达到1百万字）大约需要2元，chat模型每输出1百万个汉字（deepseek回复你的内容累计达到1百万字）大约需要8元。

（4）在"API_KEY"输入框中填入第2步中复制的DeepSeek API Key，点击"保存"按钮。

4、 使用DeepSeek功能

（1）配置完成后，点击WPS界面中的"OfficeAI"选项卡，即可使用DeepSeek的各种功能，如AI校对、文案生成、润色、翻译等。

例如，在文档中选中需要处理的文字，点击"生成"按钮，DeepSeek会开始处理并生成结果，结果可以直接导出到文档中。

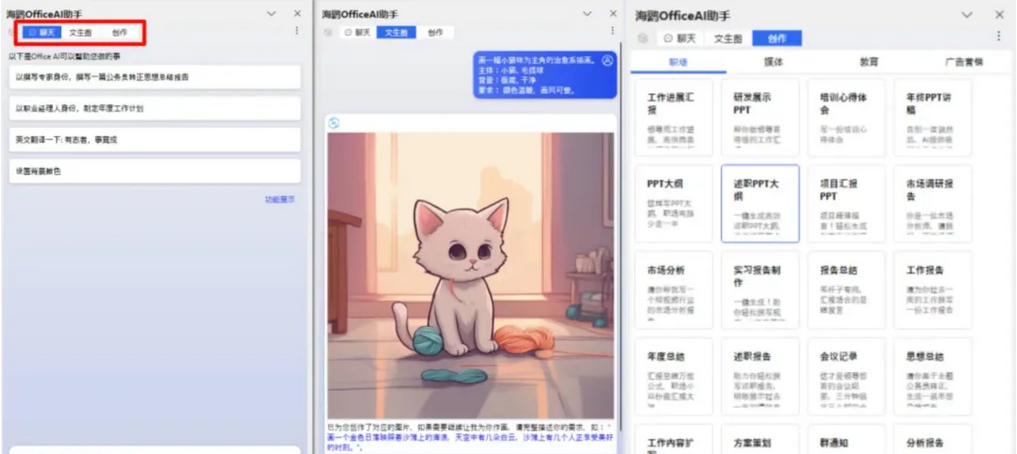
（2）在WPS文本的右侧边栏，会显示OfficeAI助手，分为聊天、文生图、创作三个部分。

在聊天栏中，可以在deepseek返回的内容最下方点击"导到左侧"，将内容直接复制到文档中。

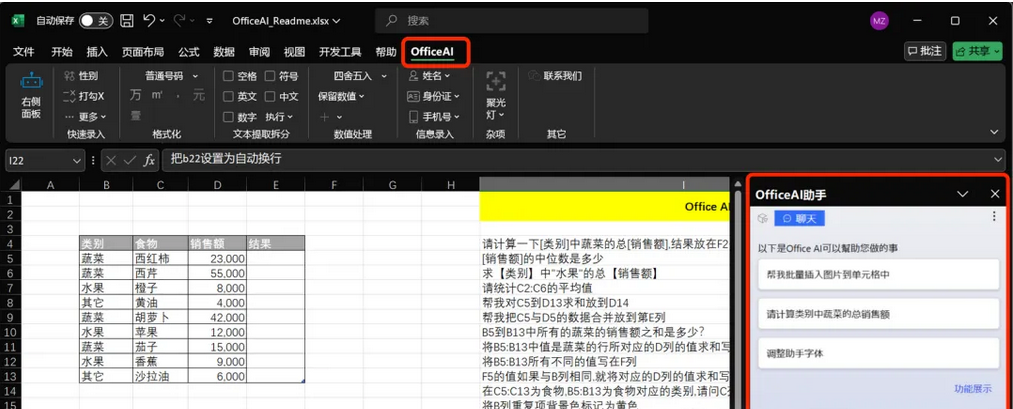
（3）在WPS表格中，也会有相应的"OfficeAI"选项卡。

5、在Office的Word、Excel中使用deekseek的方法与上面的步骤相同，配置成功后会显示"OfficeAI"选项卡。

需要提醒一点：近期deepseek流量过大，每天每个账号有进行限流。如果你问的问题比较复杂，可能只会回复你一个问题，然后就一直提示"服务器繁忙"，需要等到第二天才会继续回复你的问题。如果你问的问题比较简单，那么可能会回复你三四个问题，之后仍然会变成一直提示"服务器繁忙"的状态。

​