今天开始学习并查集
什么是并查集呢?顾名思义,就是动态维护一个方便进行合并和查找的集合
我们采用的是树状结构 也就是说,对于一开始的每个元素 它的爸爸是它自己
然后在输入两个元素的从属关系的时候,通过路径压缩,把它的爸爸直接连到根节点
因为我们只关心这个元素在这棵树里的从属关系,因此它的位置无关紧要。
当合并的时候,只需将一棵树的根节点的爸爸设置成为另一棵树的根节点。
查询的时候,查找这两个元素在不在同一棵树里(根节点一不一样)就可以。
下面是合并的代码:
int get(int x){if(fa[x]==x) return x;return fa[x]=get(fa[x]);//路径压缩 把每个访问过的元素都直接连到根
}
void merge(int x,int y){fa[get(x)]=get(y);return ;
}
查询就不用说了 放一下模版题:
P3367 【模板】并查集
题目背景
自 2025 年 1 月 21 日,本题测试数据范围更新,详见:https://www.luogu.com.cn/discuss/1045596
这意味着现存题解的代码可能无法通过本题,管理组将会在 2025 年 2 月处理。
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。
输入格式
第一行包含两个整数 \(N,M\) ,表示共有 \(N\) 个元素和 \(M\) 个操作。
接下来 \(M\) 行,每行包含三个整数 \(Z_i,X_i,Y_i\) 。
当 \(Z_i=1\) 时,将 \(X_i\) 与 \(Y_i\) 所在的集合合并。
当 \(Z_i=2\) 时,输出 \(X_i\) 与 \(Y_i\) 是否在同一集合内,是的输出
Y ;否则输出 N 。
输出格式
对于每一个 \(Z_i=2\) 的操作,都有一行输出,每行包含一个大写字母,为 Y 或者 N 。
输入输出样例 #1
输入 #1
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
输出 #1
N
Y
N
Y
说明/提示
对于 \(15\%\) 的数据,\(N \le 10\),\(M \le 20\)。
对于 \(35\%\) 的数据,\(N \le 100\),\(M \le 10^3\)。
对于 \(50\%\) 的数据,\(1\le N \le 10^4\),\(1\le M \le 2\times 10^5\)。
对于 \(100\%\) 的数据,\(1\le N\le 2\times 10^5\),\(1\le M\le 10^6\),\(1 \le X_i, Y_i \le N\),\(Z_i \in \{ 1, 2 \}\)。
代码如下:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,m;
int x,y,z;
int fa[200005];
int get(int x){if(fa[x]==x) return x;return fa[x]=get(fa[x]);//路径压缩 把每个访问过的元素都直接连到根
}
void merge(int x,int y){fa[get(x)]=get(y);return ;
}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=200005;i++) fa[i]=i;for(int i=1;i<=m;i++){scanf("%d%d%d",&z,&x,&y);if(z==1){merge(x,y);}if(z==2){if(get(x)==get(y)) cout<<'Y'<<endl;else cout<<'N'<<endl; }}system("pause");return 0;
}
好的 现在你已经学会并查集了 下面我们来看一道拓展题:
P1955 [NOI2015] 程序自动分析
题目描述
在实现程序自动分析的过程中,常常需要判定一些约束条件是否能被同时满足。
考虑一个约束满足问题的简化版本:假设 \(x_1,x_2,x_3,\cdots\) 代表程序中出现的变量,给定 \(n\) 个形如 \(x_i=x_j\) 或 \(x_i\neq x_j\) 的变量相等/不等的约束条件,请判定是否可以分别为每一个变量赋予恰当的值,使得上述所有约束条件同时被满足。例如,一个问题中的约束条件为:\(x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1\),这些约束条件显然是不可能同时被满足的,因此这个问题应判定为不可被满足。
现在给出一些约束满足问题,请分别对它们进行判定。
输入格式
输入的第一行包含一个正整数 \(t\),表示需要判定的问题个数。注意这些问题之间是相互独立的。
对于每个问题,包含若干行:
第一行包含一个正整数 \(n\),表示该问题中需要被满足的约束条件个数。接下来 \(n\) 行,每行包括三个整数 \(i,j,e\),描述一个相等/不等的约束条件,相邻整数之间用单个空格隔开。若 \(e=1\),则该约束条件为 \(x_i=x_j\)。若\(e=0\),则该约束条件为 \(x_i\neq x_j\)。
输出格式
输出包括 \(t\) 行。
输出文件的第 \(k\) 行输出一个字符串 YES 或者 NO(字母全部大写),YES 表示输入中的第 \(k\) 个问题判定为可以被满足,NO 表示不可被满足。
输入输出样例 #1
输入 #1
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1
输出 #1
NO
YES
输入输出样例 #2
输入 #2
2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0
输出 #2
YES
NO
说明/提示
【样例解释1】
在第一个问题中,约束条件为:\(x_1=x_2,x_1\neq x_2\)。这两个约束条件互相矛盾,因此不可被同时满足。
在第二个问题中,约束条件为:\(x_1=x_2,x_1 = x_2\)。这两个约束条件是等价的,可以被同时满足。
【样例说明2】
在第一个问题中,约束条件有三个:\(x_1=x_2,x_2= x_3,x_3=x_1\)。只需赋值使得 \(x_1=x_2=x_3\),即可同时满足所有的约束条件。
在第二个问题中,约束条件有四个:\(x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1\)。由前三个约束条件可以推出 \(x_1=x_2=x_3=x_4\),然而最后一个约束条件却要求 \(x_1\neq x_4\),因此不可被满足。
【数据范围】
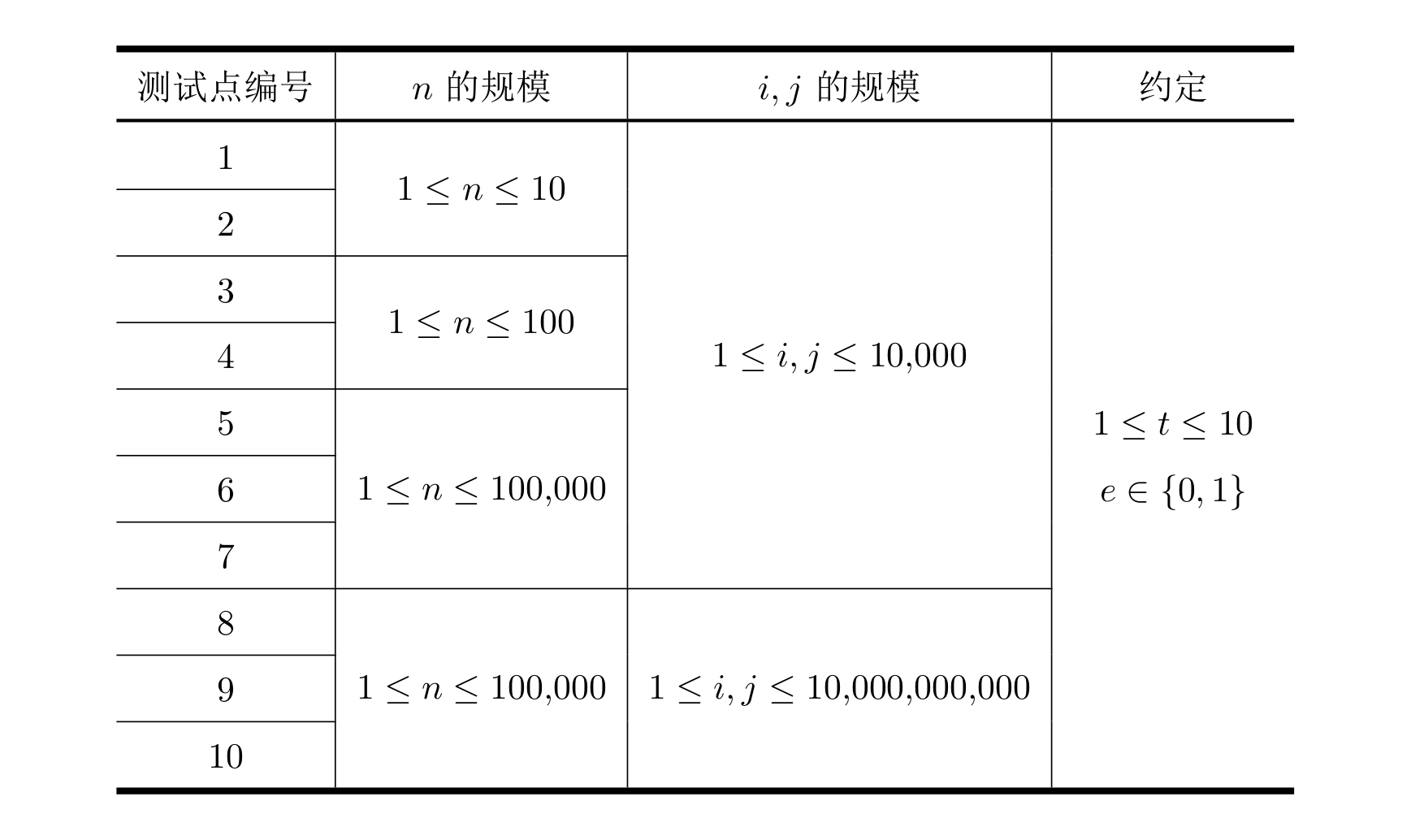
所有测试数据的范围和特点如下表所示:
勘误:测试点 \(8 \sim 10\) 的 \(i, j\) 约束为 \(1 \leq i, j \leq 10^9\),而不是下图中的 \(10^{10}\)。
解法&&个人感想
我们在这道题里主要想到的是 既然有相等关系和不相等关系
那么相等关系就相当于合并 不相等就相当于一次查找
但是本题有一个很毒瘤的数据就是它的范围到了\(10^9\)
这个时候怎么办?因为n的数据比较小 我们决定采用一种全新的方法:
离散化!
所谓离散化,就是把无限的空间对应到有限空间的映射,从而忽略其绝对大小关系而取其相对大小关系的算法
说起来比较玄乎,那么怎么实现呢?
比如有n个数,通过操作把这n个数(不管多大)全部对应到1~n的新数组里
这就叫离散化
而离散化通常分为三步
1.去重(即去掉数组里的重复数值)
2.排序(构建严格大小关系 与1~n的单增对应)
3.查找(把原来的大数赋成小数,通常用STL的二分)
贴一段经典代码:
const int N=1e5+7;
int t[N],a[N];
int main()
{cin>>n;for(int i=1;i<=n;i++)cin>>a[i],t[i]=a[i];sort(t+1,t+n+1);m=unique(t+1,t+n+1)-t-1;for(int i=1;i<=n;i++)a[i]=lower_bound(t+1,t+m+1,a[i])-t;
}
顺便说一下 这里的unique函数表示从t数组的1~n+1里面去重(把重复数值挪到最后),然后减去一个地址,得到不重复数值的数量
下面我们放代码,对于新人来说可能一开始接触结构体的并查集会有点迷糊
多想想就可以了
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int t,n,tot,flag;
int fa[1000005];
int lsh[2100000];
struct node{int x,y,z;
};
node q[1000005];
bool cmp(node a,node b){return a.z>b.z;
}
int get(int x){if(fa[x]==x) return x;return fa[x]=get(fa[x]);
}
void merge(int x,int y){fa[get(x)]=get(y);return ;
}
int main(){scanf("%d",&t);for(int i=1;i<=t;i++){scanf("%d",&n);memset(fa,0,sizeof(fa));memset(lsh,0,sizeof(lsh));memset(q,0,sizeof(q));tot=0;flag=0;for(int j=1;j<=n;j++){scanf("%d%d%d",&q[j].x,&q[j].y,&q[j].z);lsh[++tot]=q[j].x;lsh[++tot]=q[j].y;}sort(lsh+1,lsh+tot+1);int m=unique(lsh+1,lsh+tot+1)-lsh-1;for(int j=1;j<=m;j++) fa[j]=j;for(int j=1;j<=n;j++){q[j].x=lower_bound(lsh+1,lsh+m+1,q[j].x)-lsh-1;q[j].y=lower_bound(lsh+1,lsh+m+1,q[j].y)-lsh-1;}sort(q+1,q+1+n,cmp);for(int j=1;j<=n;j++){if(q[j].z==1){merge(q[j].x,q[j].y);}if(q[j].z==0){if(get(q[j].x)==get(q[j].y)){flag=1;cout<<"NO"<<endl;break;}}}if(flag==0) cout<<"YES"<<endl;}system("pause");return 0;
}