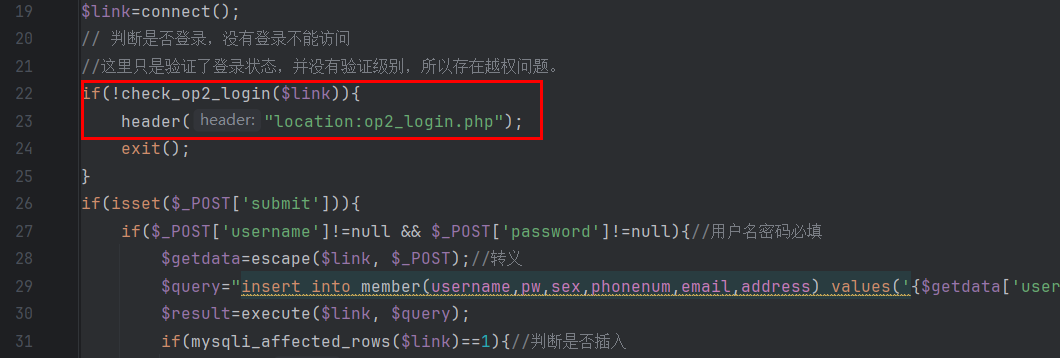
CF576A Vasya and Petyas Game 题解

CF576A Vasya and Petya's Game

数论思维题。

根据唯一分解定理，可以知道，如果一个数的各个质因数的数量确定了，这个数也就确定了。

每次询问的中，如果 \(x\) 是 \(y\) 的倍数，证明 \(x\) 中含 \(y\) 的所有质因数。我们可以枚举质数，判定 \(x\) 能否整除这个质数，就可以判断 \(x\) 是否含有这个质因数。

但是这还不能完全确定 \(x\)，因为这样只能确定是否有某个质因数，而不能确定质因数的数量。为了确定质因数的数量，我们可以把这个质数（设 \(a\) 为这个质数）的 \(b\) 次方都枚举一遍，同时保证 \(a^b\le n\)。因为由乘方的定义，得 \(a^b\) 中含有 \(b\) 个 \(a\)，如果 \(x\) 是 \(a^b\) 的倍数，证明 \(x\) 中至少含有 \(b\) 个质因数 \(a\)。把 \(\le n\) 的这类数字都枚举一遍，就可以确定 \(x\) 各个质因子的个数了。

所以，我们先用线性筛筛出 \(\le n\) 的质数，然后根据上文所述计算输出即可。

完整代码

#include <bits/stdc++.h>
using namespace std;
int n,pri[70000],ansd[10000];
bool a[700000];
int linear(bool a[],int pri[],int n)
{int cnt=0;a[1]=1;for(int i=2;i<=n;i++){if(!a[i])pri[cnt++]=i;for(int j=0;j<cnt&&i*pri[j]<=n;j++){if(!a[i*pri[j]])a[i*pri[j]]=1;if(i%pri[j]==0)break;}}return cnt;
}int main()
{int ans=0;scanf("%d",&n);int cnt=linear(a,pri,n);for(int i=0;i<cnt;i++){int now=1;while(now*pri[i]<=n)now*=pri[i],ansd[ans++]=now;}printf("%d\n",ans);for(int i=0;i<ans;i++)printf("%d ",ansd[i]);return 0;
}

AC记录