用网络流建模解决最大密度子图问题

在图论中，子图是由原图的一部分节点和这些节点之间的边构成的图。图的密度通常是指图中边的数量与节点的数量之比。形式化地，对于一个图 $ H = (V, E) $，其密度定义为：

\[\text{密度}(H) = \frac{|E|}{|V|} \]

其中，$ |E| $ 表示图 $ H $ 中的边的数量，$ |V| $ 是图 $ H $ 中节点的数量。图的密度即“边数/点数”。

最大密度子图问题要求这样一个目标：从给定的图中找出一个子图，使得该子图的密度最大。

最大密度子图问题在多个领域中都有重要的应用，特别是在社交网络分析、生物信息学、推荐系统等领域。通过找出一个图中最大密度的子图，我们能够捕捉到图中的重要结构或紧密联系的节点子集。这些子集往往包含了图中最具有信息价值的部分。

二分猜测答案和最大流验证

直接求解最大密度子图是一个 NP 难题。但通过网络流构造与二分法，我们可以在多项式时间内高效求解。

假设最大密度为 \(g^*\)，我们通过二分猜测一个候选值 \(g\)，并检验是否存在子图 \(S\) 达到此密度，通过二分法不断调整 \(g\)，直至收敛到 \(g^*\)。

网络流构造：将密度检验映射为最小割

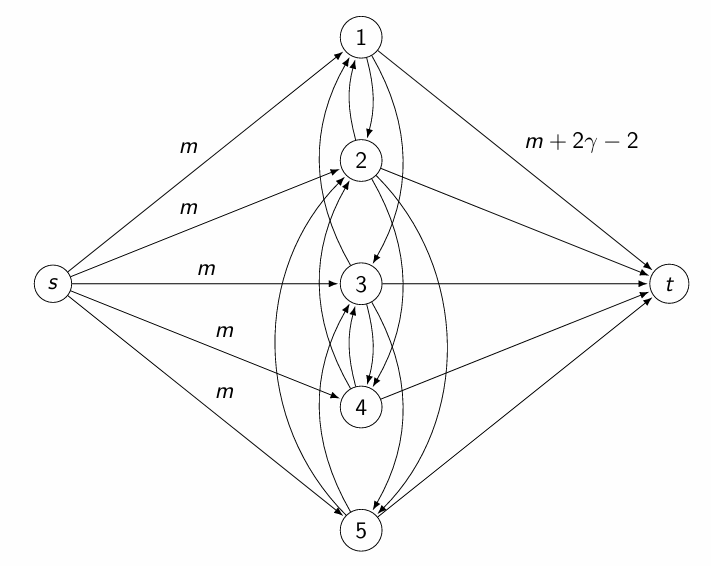
对每个猜测的 \(g\)，我们构造一个流网络，使得其最小割对应密度至少为 \(g\) 的子图存在性。网络构造如下：

顶点与边的定义

• 源点 \(s\) 和汇点 \(t\)：在原图外新添加两个点，用于划分子图候选集合 \(S\)（与 \(s\) 连通）和非候选集合 \(T\)（与 \(t\) 连通）。
• 边容量设计：
  1. 源点 \(s\) 到每个顶点 \(v\)：容量为 \(m\)（原图总边数）。
  2. 每个顶点 \(v\) 到汇点 \(t\)：容量为 \(m + 2g - \text{deg}(v)\)（\(\text{deg}(v)\) 为顶点度数）。
  3. 原图中的边 \((u, v)\)：拆分为两条有向边 \(u \to v\) 和 \(v \to u\)，容量均为 \(1\)。

为什么这么做？

• 顶点到汇点的边：容量 \(m + 2g - \text{deg}(v)\) 平衡了顶点选择的成本。度数高的顶点（可能贡献更多边）到 \(t\) 的容量较低，更容易被保留在 \(S\) 中。
• 原边的双向容量：若子图 \(S\) 包含边 \((u, v)\)，则 \(u\) 和 \(v\) 均属于 \(S\)，双向边不会被切割；否则至少一条边被切断，代价为 \(1\)，对应损失这条边对密度的贡献。

接下来运行最大流最小割算法。

割容量公式

对这样构造的图的任意割 \((S \cup \{s\}, T \cup \{t\})\)，其总容量（也等于最小割）为：

\[\begin{aligned} C &= \underbrace{m|T|}_{\text{源到非候选集}} + \underbrace{\sum_{v \in S} \left(m + 2g - \text{deg}(v)\right)}_{\text{候选集到汇点}} + \underbrace{2c(S, T)}_{\text{原边切割}} \\ &= mn + 2g|S| - 2|E(S)| + 2c(S, T), \end{aligned} \]

其中 \(c(S, T)\) 是原图中 \(S\) 到 \(T\) 的边数，\(n\) 为总顶点数。当 \(C < mn\) 时，化简可得：

\[g|S| - |E(S)| + c(S, T) < 0 \implies |E(S)| > g|S| - c(S, T). \]

由于 \(c(S, T) \geq 0\)，此时至少存在子图 \(S\) 满足 \(|E(S)| \geq g|S|\)，即当前猜测 \(g\) 可行。

若选取的 \(g\) 足够小，到汇点的容量不足，源点出发的所有边不能灌满。最小割顶点更倾向于划入源点以避免高切割代价。当 \(g\) 较大时，容量将总是 \(mn\)，当最小割容量首次达到 \(mn\)，此时对应的 \(g\) 即为最大密度。此时最小割中所有的点及其互相相连的边刚好贯通所有流量，他们就构成了我们要的最大密度子图。

所以，若当前网络的最小割容量 \(C < mn\)，说明存在密度超过 \(g\) 的子图，可尝试增大 \(g\)；否则需减小 \(g\)。最终当猜测区间足够小时结束算法，得到答案，而最终最小割对应的顶点集合 \(S\) 即为最大密度子图。